重温 Java 21 之向量 API

向量 API 最初由 JEP 338 提出，并作为孵化 API 集成到 Java 16 中，在 Java 17 到 20 中，又经过了 JEP 414、JEP 417、JEP 426、JEP 438 四次的孵化，这次在 Java 21 中，已经是第六次孵化了。

向量 API 又被称为 Vector API ，要注意，这里讲的并不是 Java 中的 Vector 集合类，而是一种专门用于向量计算的全新 API。尽管这个 API 还在孵化期，并没有正式发布，但是这项技术很值得我们提前学习和了解，因为这项技术代表了 Java 语言发展的一个重要方向，在未来一定会有着重要的影响。随着生成式人工智能的发展，Embedding 技术也如日中天，它将各种类型的数据（如文本、图像、声音等）转换为高维数值向量，从而实现对数据特征和语义信息的表示。Embedding 技术在个性化推荐、多模态检索和自然语言处理等领域中发挥着重要作用，而这些场景都离不开向量计算。

什么是向量？

向量是数学和物理学中的一个基本概念，具有大小和方向两个属性，比如物理学中的力就是向量。向量可以有多种不同的表示方式：

在代数中，一般印刷用黑体的小写英文字母来表示（比如 a 、b 、c 等），手写用在 a、b、c 等字母上加一箭头（→）表示；
在几何中，向量可以形象化地表示为带箭头的线段，箭头所指的方向代表向量的方向，线段长度则代表向量的大小；
在坐标系中，向量可以用点的坐标位置来表示，比如平面直角坐标系中的向量可以记为 (x, y)，空间直角坐标系中的向量可以记为 (x, y, z)，多维空间以此类推；此外，向量也可以使用矩阵来表示；
在计算机科学中，向量可以被理解为一个数字列表或数组，这在编程语言中尤为常见。

和向量这个概念相对应的，还有标量、矩阵、张量等概念，这几个概念可以代表不同的维度，一般用点线面体来类比：

点------标量（scalar）
线------向量（vector）
面------矩阵（matrix）
体------张量（tensor）

标量计算 vs. 向量计算

标量就是一个数字，在 Java 中通常可以表示为一个整数或浮点数等，我们所熟知的算术运算基本上都是作用于标量之上的，比如下面的代码对 a 和 b 两个标量求和：

java 复制代码

int a = 1;
int b = 1;
int c = a + b;

如果将 a 和 b 换成向量，也就是数组，该如何求和呢？最简单的方法是使用 for 循环依次相加数组中对应的元素：

java 复制代码

int[] a = new int[] {1, 2, 3, 4};
int[] b = new int[] {1, 2, 3, 4};
int[] c = new int[4];
for (int i = 0; i < a.length; i++) {
  c[i] = a[i] + b[i];
}

很显然这不是什么高明的做法，仔细观察上面的代码就会发现，对于数组中每个元素的相加是互不影响的，那么我们能不能并行计算呢？一种有效的解决方法是使用 并行流（Parallel Stream）：

java 复制代码

IntStream.range(0, a.length)
  .parallel()
  .forEach(i -> c[i] = a[i] + b[i]);

另一种解决方法就是我们将要学习的 向量 API（Vector API）：

java 复制代码

IntVector aVector = IntVector.fromArray(IntVector.SPECIES_128, a, 0);
IntVector bVector = IntVector.fromArray(IntVector.SPECIES_128, b, 0);
IntVector cVector = aVector.add(bVector);

注意，由于向量 API 并没有正式发布，运行时需要手动加上 jdk.incubator.vector 模块：

arduino 复制代码

$ java --add-modules jdk.incubator.vector VectorDemo.java

向量 API 定义了专门的向量类，比如这里的 IntVector，并提供了 fromArray 方法方便我们将数组转换为向量，然后再通过 aVector.add(bVector) 执行两个向量的加法运算。

除了加法运算，向量 API 还提供了一组方法来执行各种其他的向量计算：

算术运算（Arithmetic Operations）
- 加法：vector1.add(vector2)
- 减法：vector1.sub(vector2)
- 乘法：vector1.mul(vector2)
- 除法：vector1.div(vector2)
逐元素操作（Element-Wise Operations）
- 绝对值：vector.abs()
- 负数：vector.neg()
- 平方根：vector.sqrt()
- 指数：vector.exp()
- 对数：vector.log()
规约运算（Reductions）
- 元素之和：vector.reduce(VectorOperators.ADD)
- 最小元素：vector.reduce(VectorOperators.MIN)
- 最大元素：vector.reduce(VectorOperators.MAX)
- 平均值：vector.reduce(VectorOperators.ADD).mul(1.0 / vector.length())
逻辑运算（Logical Operations）
- 与：vector1.and(vector2)
- 或：vector1.or(vector2)
- 非：vector.not()
比较操作（Comparisons）
- 等于：vector1.eq(vector2)
- 小于：vector1.lt(vector2)
- 大于：vector1.compare(VectorOperators.GT, vector2)

单指令多数据（SIMD）

使用向量 API 来执行向量计算，不仅代码精简，容易理解，而且它还有另一个好处，那就是性能提升。尽管使用并行流也能提升一定的性能，但是并行流和向量 API 是两种完全不同的优化技术，前者使用多线程在不同的 CPU 核上并行计算，而后者通过 SIMD 技术，在单个 CPU 周期内对多个数据同时执行相同操作，从而达到并行计算的目的。

SIMD（Single Instruction, Multiple Data，单指令多数据） 是一种并行处理技术，它的核心思想是将一个控制器与多个处理单元结合在一起，使得这些处理单元可以针对不同的数据同时执行相同的操作，简单来说就是一个指令能够同时处理多个数据。这与传统的 SISD（Single Instruction, Single Data，单指令单数据） 形成对比，在后者中，一个指令只能处理一个数据。

在上面那个向量求和的例子中，我们先是使用 for 循环实现：

java 复制代码

for (int i = 0; i < a.length; i++) {
  c[i] = a[i] + b[i];
}

数组中的每个元素将使用（大致）1 个 CPU 指令进行计算，这意味着我们需要 4 个指令或 4 个 CPU 周期才能完成计算，这就是典型的 SISD。而使用向量 API 可以将向量的计算编译为对应 CPU 架构上的 SIMD 指令集，只要 1 个指令即可完成向量计算：

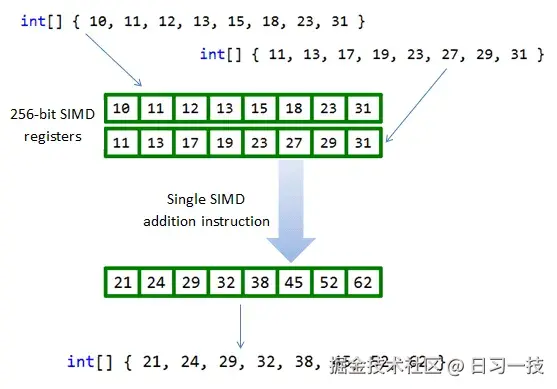
在实际应用中，许多现代处理器都支持 SIMD 指令集，如 Intel 的 MMX 、SSE 和 AVX ，ARM 的 NEON 和 SVE 等，这些指令集能够显著提升程序的执行效率，特别是在需要大量数值计算的场景下。不过使用这些指令集的门槛并不低，通常涉及到汇编语言或一些特殊的函数库，比如 Intel 的跨平台函数库 IPP（Integrated Performance Primitives）或使用内置函数 (Intrinsic function) 等。

相比于传统的手写 SIMD 代码，Java 的向量 API 提供了更高的可读性和维护性，开发者可以使用熟悉的 Java 语法和类型系统，无需处理底层寄存器和指令，编写出简洁明了的、平台无关的、高性能的向量计算代码。

其实，在向量 API 提出之前，Java 已经在 SIMD 上探索了很长一段时间了，比如 HotSpot 的自动向量化（Auto-Vectorization）功能，它将标量操作转换为 超字操作（SuperWord Operations），然后再映射到 SIMD 指令。然而，这个过程完全依赖 JIT，并没有什么可靠的方法来保证编写的代码一定可以使用 SIMD 指令优化，有些代码甚至根本无法进行优化，开发人员必须深入了解 HotSpot 的自动向量化算法及其限制，才能实现可靠的性能提升。向量 API 使得这个过程完全由开发人员自己控制，因此可以写出更加可预测、更加稳健的代码。

我们可以通过 -XX:-UseSuperWord 参数关闭 HotSpot 的自动向量化功能。

使用向量 API

在学习了向量的基础知识之后，接下来我们将继续深入学习向量 API 的使用。

上面介绍向量计算时，我们已经学习了向量 API 的基本用法，使用 IntVector 实现两个向量相加。这个示例为了易于理解，做了简单处理，并没有考虑在实际使用时的边界情况，假设我们将 a 和 b 两个数组改成 10 个数字：

java 复制代码

int[] a = new int[] {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int[] b = new int[] {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
IntVector aVector = IntVector.fromArray(IntVector.SPECIES_128, a, 0);
IntVector bVector = IntVector.fromArray(IntVector.SPECIES_128, b, 0);
IntVector cVector = aVector.add(bVector);

运行后得到的结果 c 仍然是 [2, 4, 6, 8]，后面新加的数字并没有计算。这是因为每个向量的存储空间有限，并不能一次存下所有的数据。这里涉及向量 API 的一个重要概念：向量种类（Vector Species） ，它是 数据类型（Data Types） 和 向量形状（Vector Shapes） 的组合；所谓数据类型就是 Java 的基础类型，比如 byte、short、int、long 这些整数类型和 float、double 浮点类型，而所谓向量形状就是向量的位大小或位数；比如这里的向量种类为 IntVector.SPECIES_128，它代表数据类型为 int，向量形状为 128 位；而我们知道，一般情况下 int 值的大小为 32 位，所以这个向量一次只能存储 128/32 = 4 个 int 值，这也被形象地称为 通道（Lanes），表示向量一次可以处理的数据个数。

知道这一点后，我们就可以写出更加通用的向量计算代码了。首先我们需要将数据按通道数分组，然后一组一组的进行处理：

java 复制代码

int[] a = new int[] {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int[] b = new int[] {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int[] c = new int[10];
int lanes = IntVector.SPECIES_128.length();
int loopBound = IntVector.SPECIES_128.loopBound(a.length);
for (int i = 0; i < loopBound; i += lanes) {
  IntVector aVector = IntVector.fromArray(IntVector.SPECIES_128, a, i);
  IntVector bVector = IntVector.fromArray(IntVector.SPECIES_128, b, i);
  IntVector cVector = aVector.add(bVector);
  cVector.intoArray(c, i);
}
for (int i = loopBound; i < a.length; i++) {
  c[i] = a[i] + b[i];
}
IntStream.of(c).forEach(x -> System.out.println(x));

我们可以注意到，在遍历时 i 每次增加 lanes，它的值等于 IntVector.SPECIES_128.length()，也就是通道数，一般来说该值等于 4，所以我们是按 4 个一组进行处理的。但是要注意数据不一定能被通道数完全整除，比如这里 10 个数字，前 8 个可以分为两组处理掉，还剩下 2 个怎么办呢？这时我们只能使用最原始的标量计算来处理了。

此外，在实际编码时向量种类不建议写死，可以使用 IntVector.SPECIES_PREFERRED 替代，它会根据平台自动选择最合适的向量种类：

java 复制代码

static final VectorSpecies<Integer> SPECIES = IntVector.SPECIES_PREFERRED;

可以看出尽管向量 API 的使用有不少好处，但是我们也需要谨慎对待：

首先，在使用向量 API 时，数据对齐是一个重要的考虑因素，不对齐的数据访问可能会导致性能下降。开发者需要确保数据在内存中的对齐方式，以充分发挥 SIMD 指令的优势；
另外，向量 API 有硬件依赖性，它依赖于底层硬件支持的 SIMD 指令集，许多功能可能在其他平台和架构上不可用，性能也可能会有所不同。开发者需要了解目标平台的特性，并进行适当的性能优化。

小结

今天我们学习了 Java 21 中的 向量 API（Vector API），这个特性从 Java 16 开始就已引入，一直在不断演进和完善。学习内容总结如下：

向量计算基础 - 向量是数学和物理学中的基本概念，在计算机科学中被表示为数组或列表。向量计算相比标量计算，通过一次性处理多个数据元素，显著提高了计算效率，这正是现代高性能计算的关键所在；
SIMD 优势 - 向量 API 充分利用现代处理器的 SIMD（单指令多数据）指令集特性，如 Intel 的 AVX 和 ARM 的 NEON，相比于手写汇编或使用低级 Unsafe API，向量 API 提供了更高的可读性、更好的可维护性和更可靠的性能保证；
向量 API 的使用：虽然向量 API 带来了性能提升，但我们在使用时也需要关注数据对齐、硬件依赖性等问题，需要根据目标平台的特性进行适当的优化，这样才能充分发挥向量计算的优势；

随着生成式人工智能的快速发展，Embedding 技术和向量计算在推荐系统、多模态检索、自然语言处理等领域的应用日益广泛，向量 API 为 Java 在这些领域的应用提供了基础，有望推动 Java 在 AI 和数据科学领域的进一步发展。

欢迎关注

如果这篇文章对您有所帮助，欢迎关注我的同名公众号：日习一技，每天学一点新技术。

我会每天花一个小时，记录下我学习的点点滴滴。内容包括但不限于：

某个产品的使用小窍门
开源项目的实践和心得
技术点的简单解读

目标是让大家用5分钟读完就能有所收获，不需要太费劲，但却可以轻松获取一些干货。不管你是技术新手还是老鸟，欢迎给我提建议，如果有想学习的技术，也欢迎交流！