为什么0.1 + 0.2不等于0.3？一次讲透计算机的数学“Bug”

关注我的公众号：【编程朝花夕拾】，可获取首发内容。

01 引言

0.1+0.2≠0.3这样问题在程序界，可能大加都知道结论，也可能知道如何规避。但是到底是什么原因呢？

当然，我们都知道这是计算机底层二进制的问题。但是为何会这样呢？我们一起看看吧。

02 情景复现

2.1 `JavaScript`

在任意的浏览器，调出开发者模式，在控制台输入：

sh 复制代码

console.info(0.1+0.2);
console.info(0.3);
console.info(0.1+0.2 == 0.3);

下图为谷歌浏览器案例：

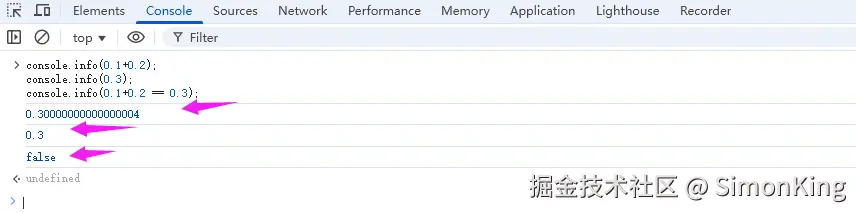
我们发现0.1+0.2 == 0.3返回的结果是false。而0.1+0.2=0.30000000000000004和0.3确实不相等。

2.2 `Java`

java 复制代码

@Test
void test01(){
    System.out.println(0.1 + 0.2);
    System.out.println(0.3);
    System.out.println(0.1 + 0.2 == 0.3);
    System.out.println("---------------------------------");
    System.out.println(new BigDecimal(0.1).add(new BigDecimal(0.2)));
    System.out.println(new BigDecimal(0.3));
    System.out.println("---------------------------------");
    System.out.println(new BigDecimal("0.1").add(new BigDecimal("0.2")));
    System.out.println(new BigDecimal("0.3"));
}

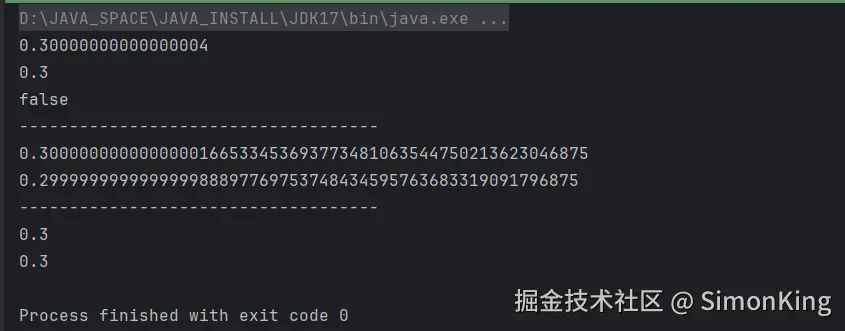
基本数据类型和BigDecimal的运算都会出现0.1+0.2≠0.3的问题。

运行结果：

03 原因分析

案例中直接打印，没有问题是因为没有参与二进制位的运算，所以不会有精度的丢失。

要了解精度问题，就要知道在计算机中如何存储二进制位的。案例中的小数为float类型，占4个字节，32位。

3.1 二进制标准

我们知道数学界有无限循环小数，也有无限不循环小数。而计算机要处理写小数，也有统一的国际标准：IEEE 754

它规定了计算机如何用二进制来表示和计算小数（浮点数）。它就像一套世界通用的"小数书写法则"，确保了在不同计算机上，同一个小数能有相同的表示，并且计算结果是可预测的。

在 IEEE 754 出现之前，不同厂商的计算机可能用不同的方式表示小数，导致程序在一台机器上运行正常，在另一台机器上结果却不一样。IEEE 754 统一了这个规则，解决了可移植性和可靠性的问题。而IEEE 754的核心思想就是科学计数法，只不过是二进制中的科学技术法。

float的32位如何划分：

部分	符号	指数	尾数
比特数	1 bit	8 bits	23 bits

符号：

占1个bit，0 表示正数，1 表示负数。也就我们常说的符号位。

指数：

占8个bit，可以标识0~255。为了能表示负指数（比如 2⁻²），IEEE 754 使用了一个"偏置值"。对于单精度，这个值是 127 。而指数位(编码指数)的计算是有公式的：编码指数 = 实际指数 + 127

尾数：

占23个bit，指的是有效数字的小数部分。在二进制科学计数法中，任何一个数（除了0）都可以表示为 1.xxxxx × 2^指数。注意，开头的那个 1 是固定的，所以为了节省一个比特，IEEE 754 规定这个 1 是"隐藏的"，不需要存储。我们只需要存储后面的 xxxxx（小数部分）即可。这叫做"隐藏位技术"

3.2 二进制位转化

我们以0.1的二进制位为例：

js 复制代码

0.1 * 2 = 0.2 -> 0
0.2 * 2 = 0.4 -> 0
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0 （从这里开始循环）

二进制位就是将整数位以此拼接。

所以0.1的二进制是：0.000110011001100110011001100110011... (循环节0011)

使用科学计数法（规格化），小数点需要香油移动4位，所以：0.1 = 1.10011001100110011001100... × 2^(-4)。这里的-4就是实际的指数位。那么计算编码指数：编码指数 = -4 + 127 = 123。转化成二进制就是01111011

尾数是23位。只需要从1.10011001100110011001100...× 2^(-4)小数点，向后截取24位。多处的以为是直接舍去还是进一，是有逻辑处理的。处理之后，最后保留23位。

10011001 10011001 1001100 1...第24位是1，后面还有，所以粘滞位为1。根据向最接近的偶数舍入（默认舍入模式）：第24位是1，且后面有非零位，所以需要向上舍入（即第23位加1）。所以，原来的23位是：10011001100110011001100 向上舍入后变为：10011001100110011001101

因此，0.1的单精度浮点数表示为：符号位：0 指数位：01111011 尾数位：10011001100110011001101 组合起来：0 01111011 10011001100110011001101

可视化展示：

tex 复制代码

31  30    23  22                                      0
┌───┬─────────┬───────────────────────────────────────┐
│ 0 │ 01111011│ 10011001100110011001101               │
└───┴─────────┴───────────────────────────────────────┘
 │     │                     │
 │     │                     └── 尾数域 (23 bits)
 │     │                         - 存储规格化后的小数部分
 │     │                         - 隐藏位为1（不存储）
 │     │
 │     └── 指数域 (8 bits)
 │         - 编码值: 123 (二进制 01111011)
 │         - 实际指数: 123 - 127 = -4
 │
 └── 符号位 (1 bit)
     - 0 表示正数

让我们验证这个位图确实表示约等于 0.1 的值：

符号 = (-1)⁰ = +1
指数 = 2⁻⁴ = 1/16
尾数 = 1 + (1×2⁻¹ + 0×2⁻² + 0×2⁻³ + 1×2⁻⁴ + ...)

计算尾数的十进制值：

js 复制代码

1.10011001100110011001101₂ = 
1 × 1 + 
1 × 0.5 + 
0 × 0.25 + 
0 × 0.125 + 
1 × 0.0625 + 
1 × 0.03125 + 
0 × 0.015625 + 
0 × 0.0078125 + 
1 × 0.00390625 + 
1 × 0.001953125 + 
... (继续所有23位)

最终结果 ≈ 1.600000023841858 乘以指数部分：1.600000023841858 × 2⁻⁴ = 0.10000000149011612

3.3 位计算

计算0.1+0.2

由上面的计算0.1=1.10011001100110011001101₂，实际指数为-4。

同理可以算出：0.2 = 1.10011001100110011001101₂，实际指数为-3。

将实际指数调整相同：

0.1 = 0.110011001100110011001101 × 2⁻³

0.2 = 1.10011001100110011001101 × 2⁻³

计算：

sh 复制代码

text

  0.110011001100110011001101  (调整后的0.1)
+ 1.10011001100110011001101   (0.2)
─────────────────────────────
 10.011001100110011001100111

规格化处理后：1.0011001100110011001100111 × 2⁻²

最终舍入处理得到：1.00110011001100110011010 × 2⁻²

验证结果：

js 复制代码

1.00110011001100110011010₂ = 
1 × 1 + 
0 × 0.5 + 
0 × 0.25 + 
1 × 0.125 + 
1 × 0.0625 + 
0 × 0.03125 + 
0 × 0.015625 + 
1 × 0.0078125 + 
1 × 0.00390625 + 
0 × 0.001953125 + 
... (继续所有23位)

最终结果 ≈ 1.199999928474426269531250000 乘以指数部分：1.199999928474426269531250000 × 2⁻² = 0.299999982118606567382812500

而0.3在计算机的存储：0.300000011920928955078125。所以值会不相等。

可以通过这个转化工具直接查看：

地址：www.h-schmidt.net/FloatConver...

04 小结

计算机底层的东西比较晦涩难懂，如有问题还挺多多包含。上面的Java案例中BigDecimal不同的构造，保存的值不一样。

java 复制代码

@Test
void test02(){
    System.out.println(new BigDecimal("0.3"));
    // 0.3

    System.out.println(new BigDecimal(0.3));
    // 0.299999999999999988897769753748434595763683319091796875
}

所以使用的BigDecimal构造的时候需要慎重，尽量使用字符串参数的构造函数。

为什么0.1 + 0.2不等于0.3？一次讲透计算机的数学“Bug”

01 引言

02 情景复现

2.1 JavaScript

2.2 Java

03 原因分析

3.1 二进制标准

3.2 二进制位转化

3.3 位计算

04 小结

2.1 `JavaScript`

2.2 `Java`