一、数据结构
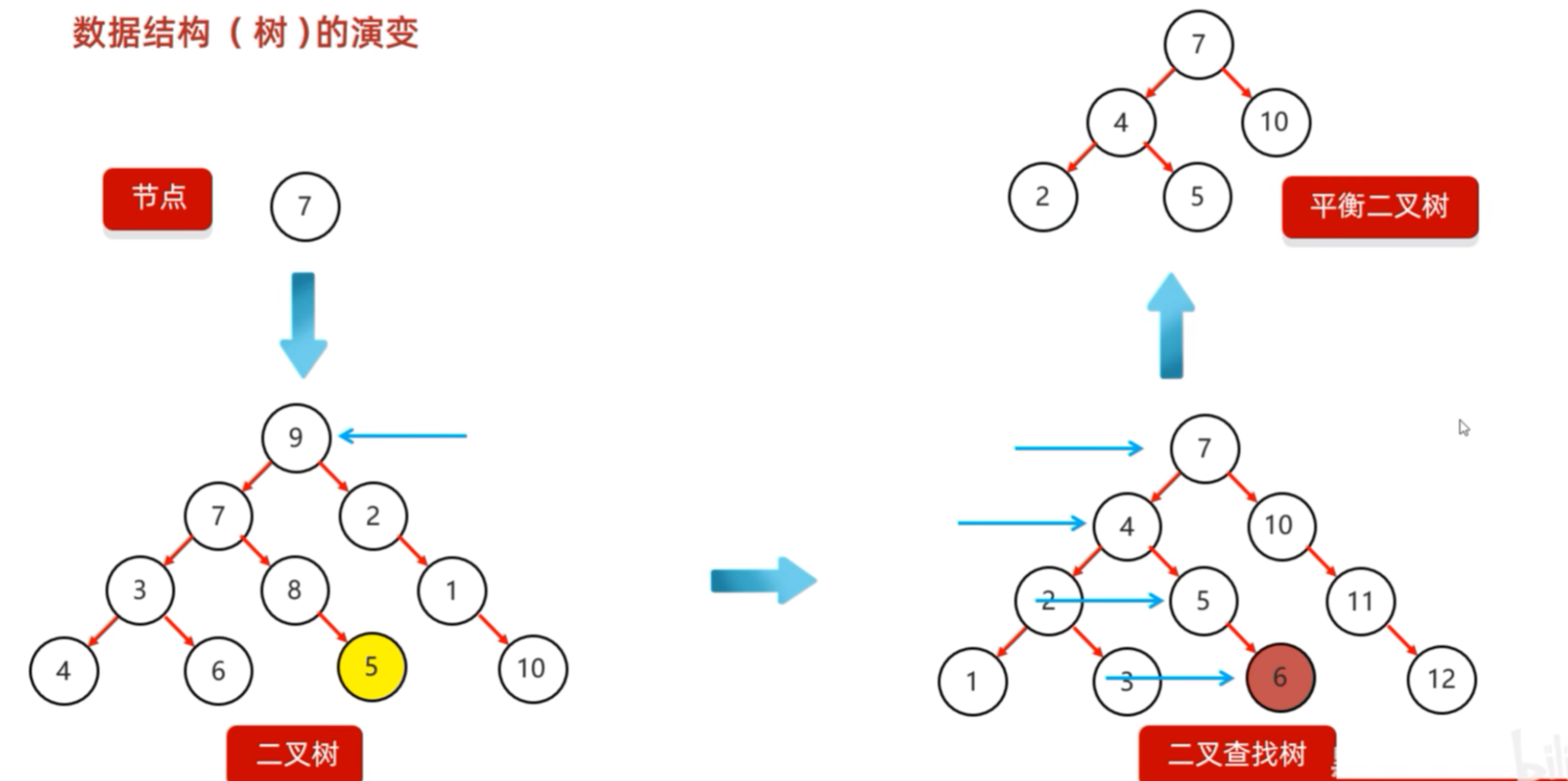
为解决上一节二叉查找树(BST)的指明缺陷,这里更加严格的平衡机制(左右子树高度差 ≤ 1)。由此引申出新的概念树------平衡二叉树。
1、平衡二叉树
1.1 什么是平衡二叉树?
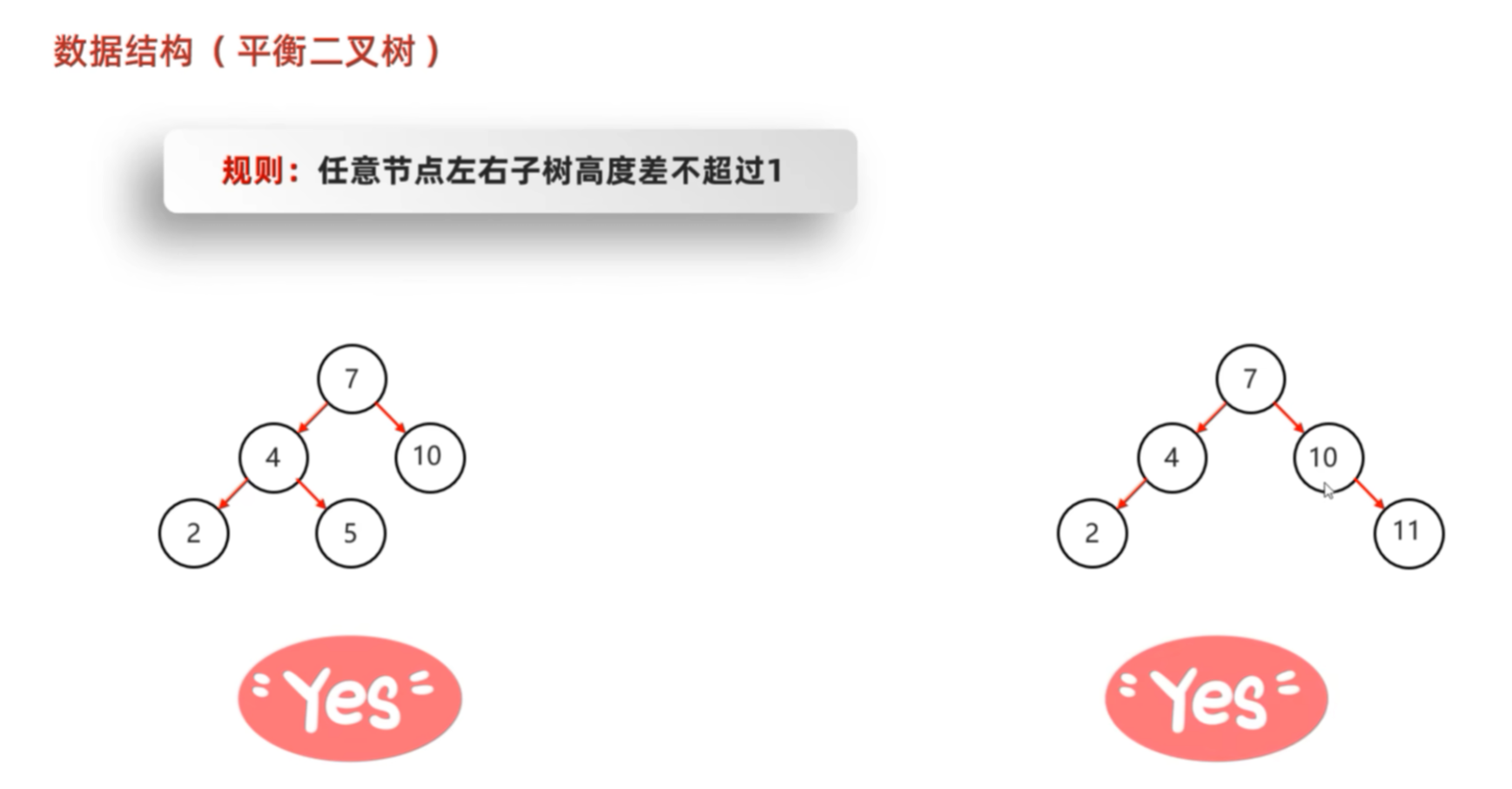
平衡二叉树(Balanced Binary Tree)是一种特殊的二叉查找树,它在插入或删除节点后,会自动调整结构,确保"左右子树高度差不超过1",从而保证操作效率始终为 O(log n)。
✅ 最经典的代表:AVL 树
- 由两位苏联科学家 Adelson-Velsky 和 Landis 在 1962 年提出
- "AVL" 就是他们名字首字母
🔑 核心定义:
对于 AVL 树中的任意一个节点 ,其左子树高度与右子树高度之差(称为"平衡因子")的绝对值 ≤ 1。
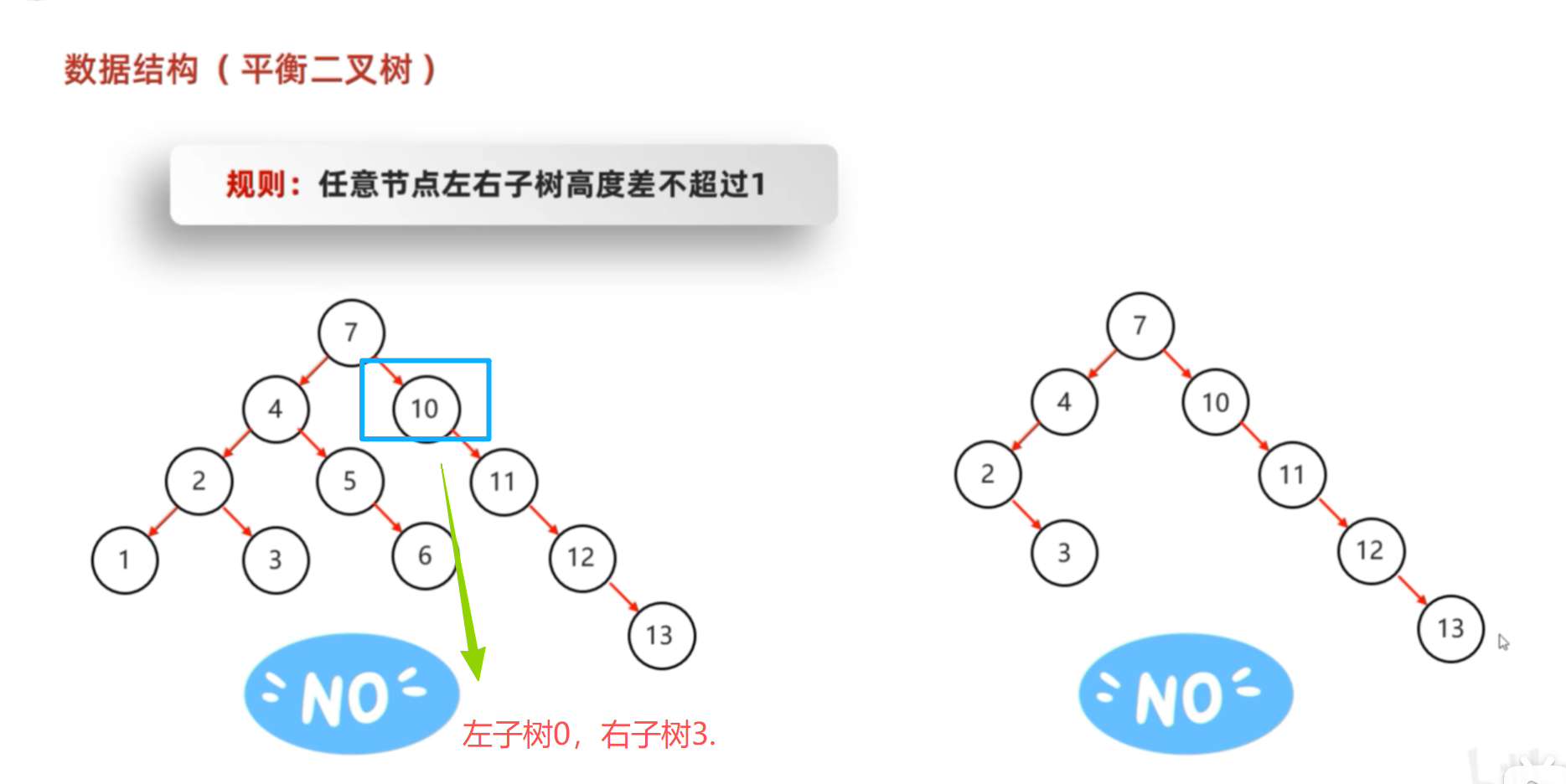
1.2 如何保持平衡?------ 旋转(Rotation)机制
当插入/删除导致某个节点平衡因子变成 2 或 -2 时,说明树"歪了",需要通过旋转把它"扶正"。
只有当添加一个新的节点之后,原本的树不再是一个平衡二叉树了,就会触发旋转机制。
🧠 旋转的本质:
- 不破坏 BST 的有序性(中序遍历结果不变!)
- 只调整父子关系和指针指向
- 像拧魔方一样局部调整结构
🌀 1. 左旋(Left Rotation)------ "把右孩子提上来"
旋转开始时,要确定添加的节点,不断的往父节点去找不平衡的节点。找到第一个"不平衡"的节点(10)之后,判断其右边的节点比左边多,所以触发左旋机制。这棵树向右倾斜,我们需要"向左拉一把" → 左旋
🎯 目标:让 11 成为新的根,10成为 11 的左孩子
步骤(以 10 为旋转中心):
- 11 成为新根
- 10的右子树 = 11的左子树(可能为空)
- 11的左子树 = 10
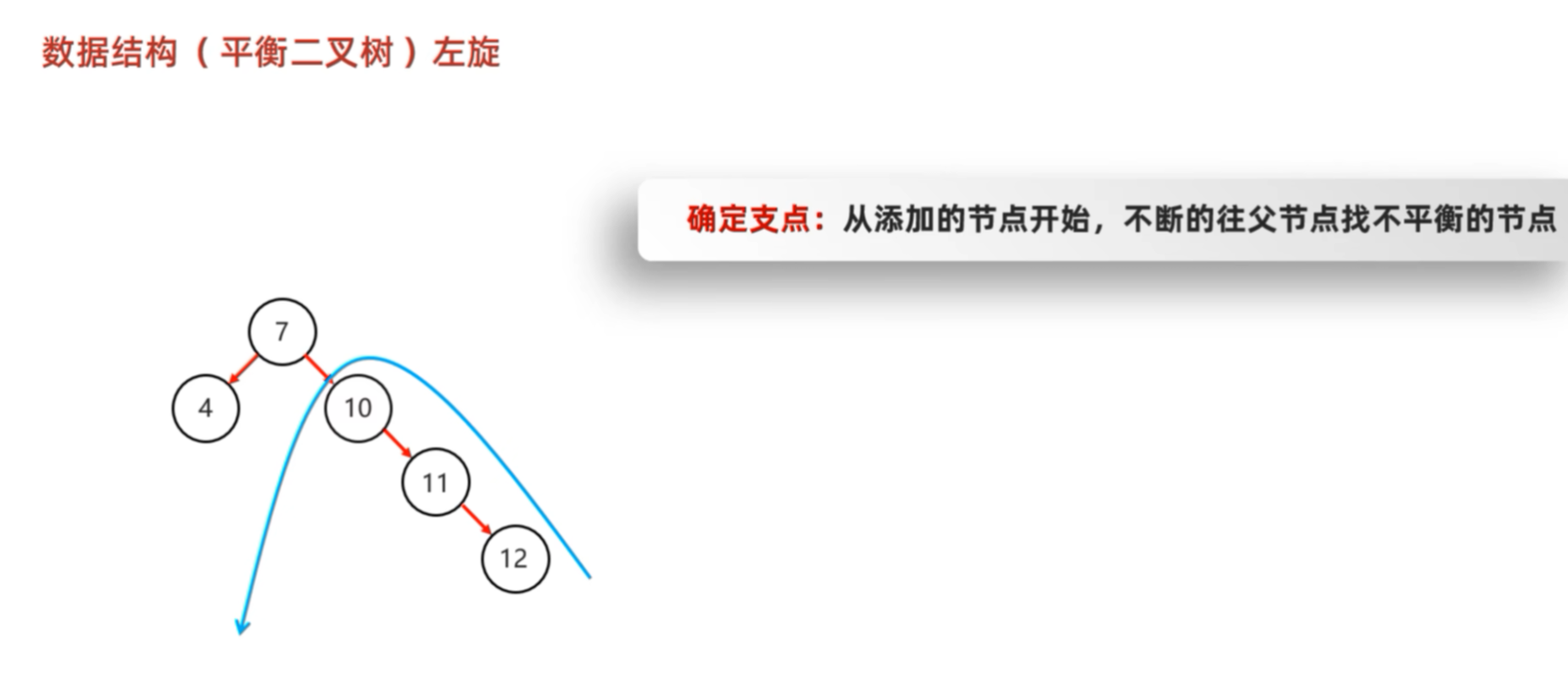

接下里看比较复杂的例子:这里找到了根节点7,判断右子节点树高-左子节点树高>=1.进行左旋机制。
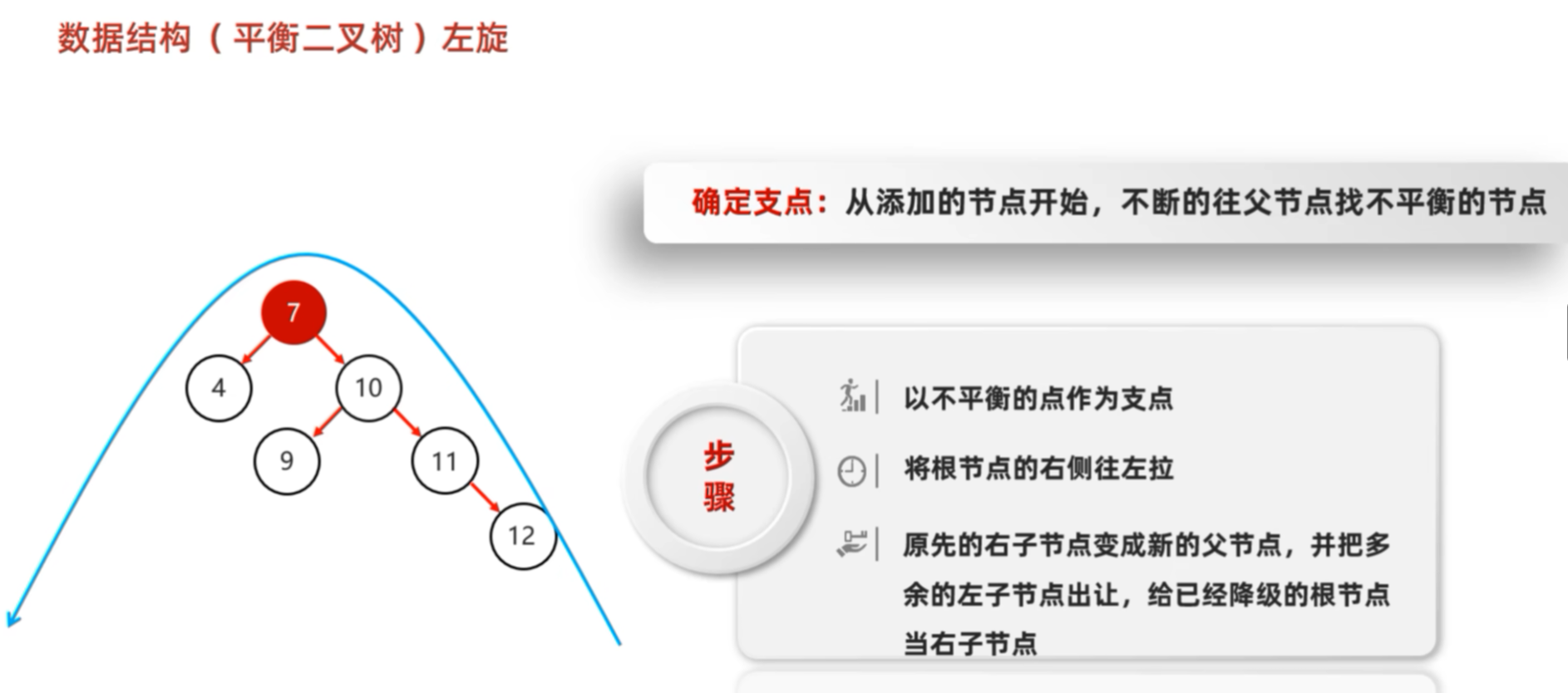

右旋反之,不再赘叙。
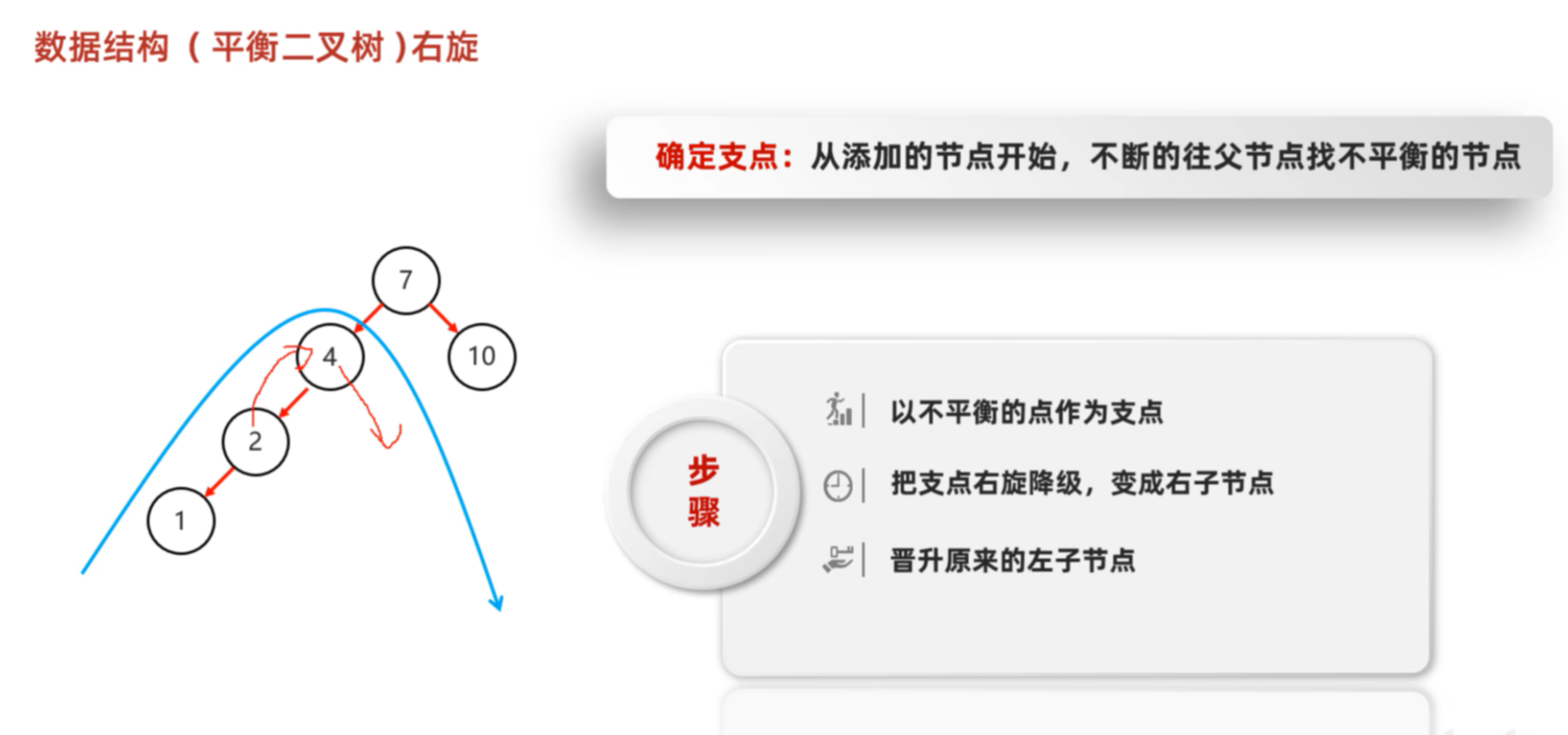
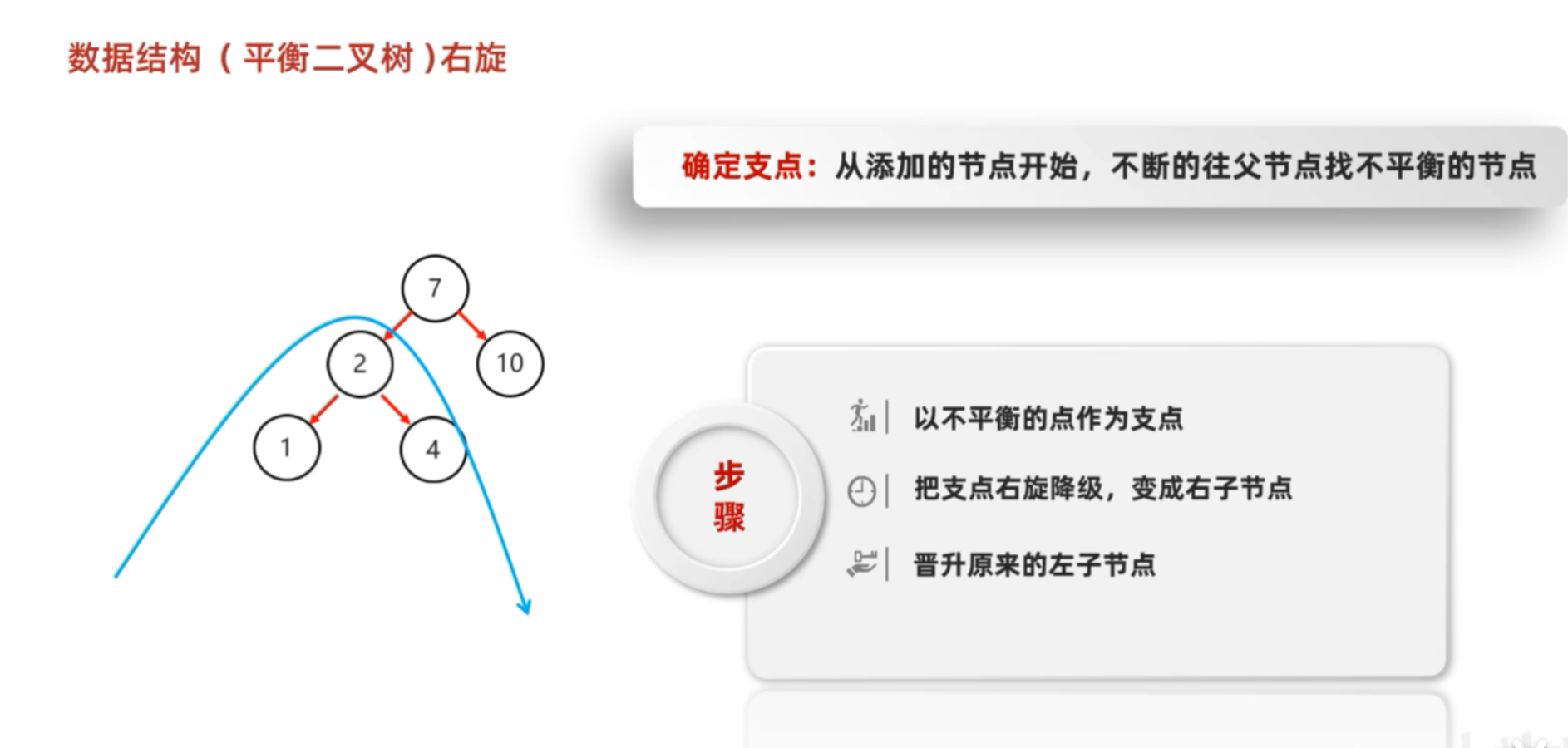
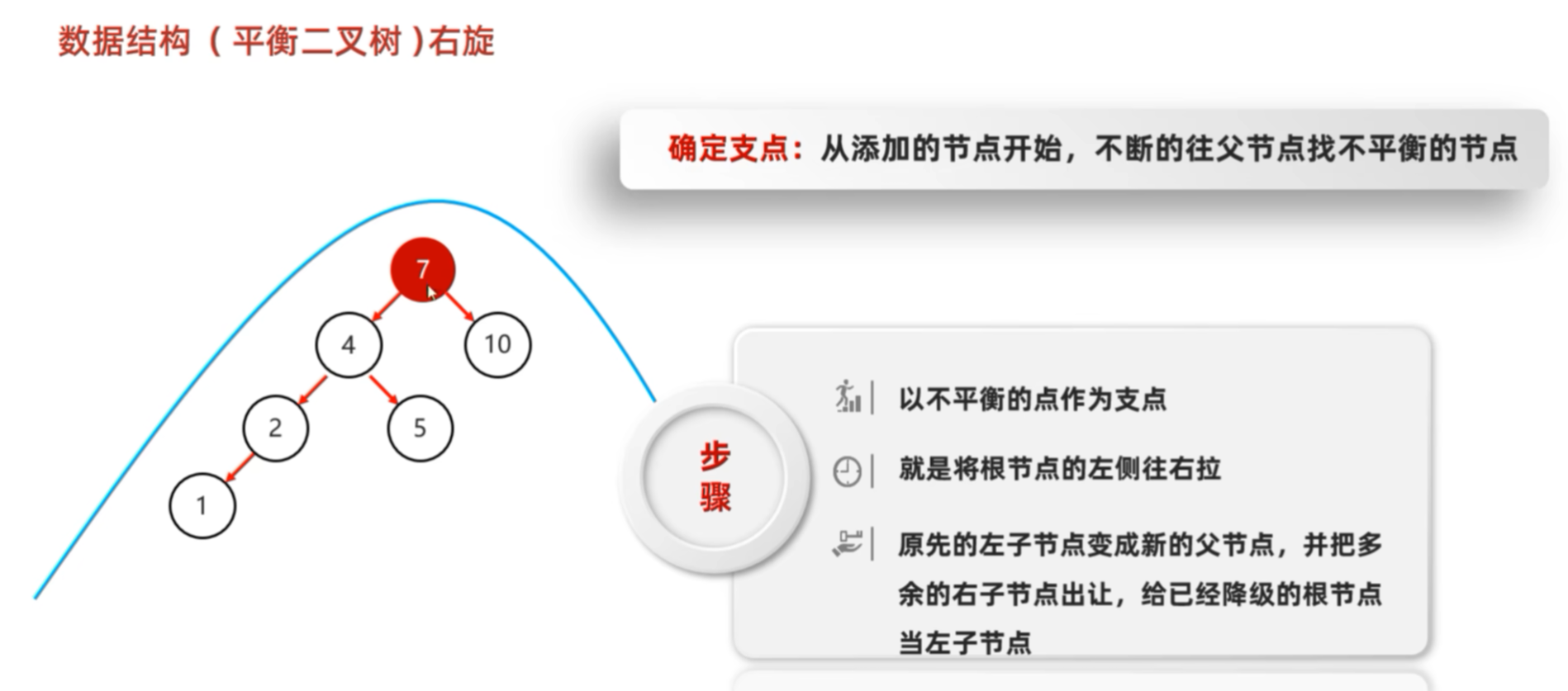
🌀 2. 右旋(Right Rotation)------ "把左孩子提上来"
🎯 场景:左子树太重(左边太长)
需要"向右推一把" → 右旋
步骤(以 4 为旋转中心):
- 2 成为新根
- 4 的左子树 = 2 的右子树
- 2 的右子树 = 4
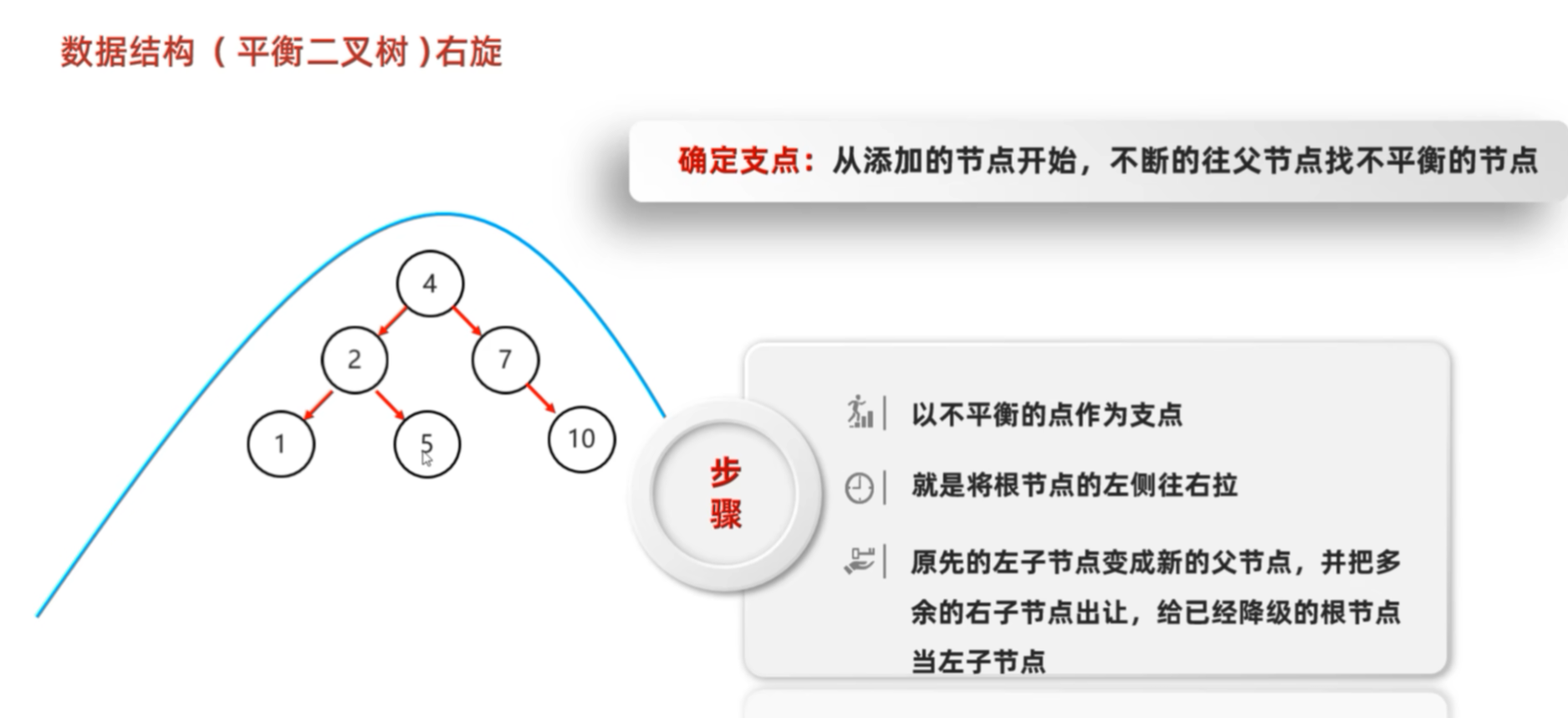
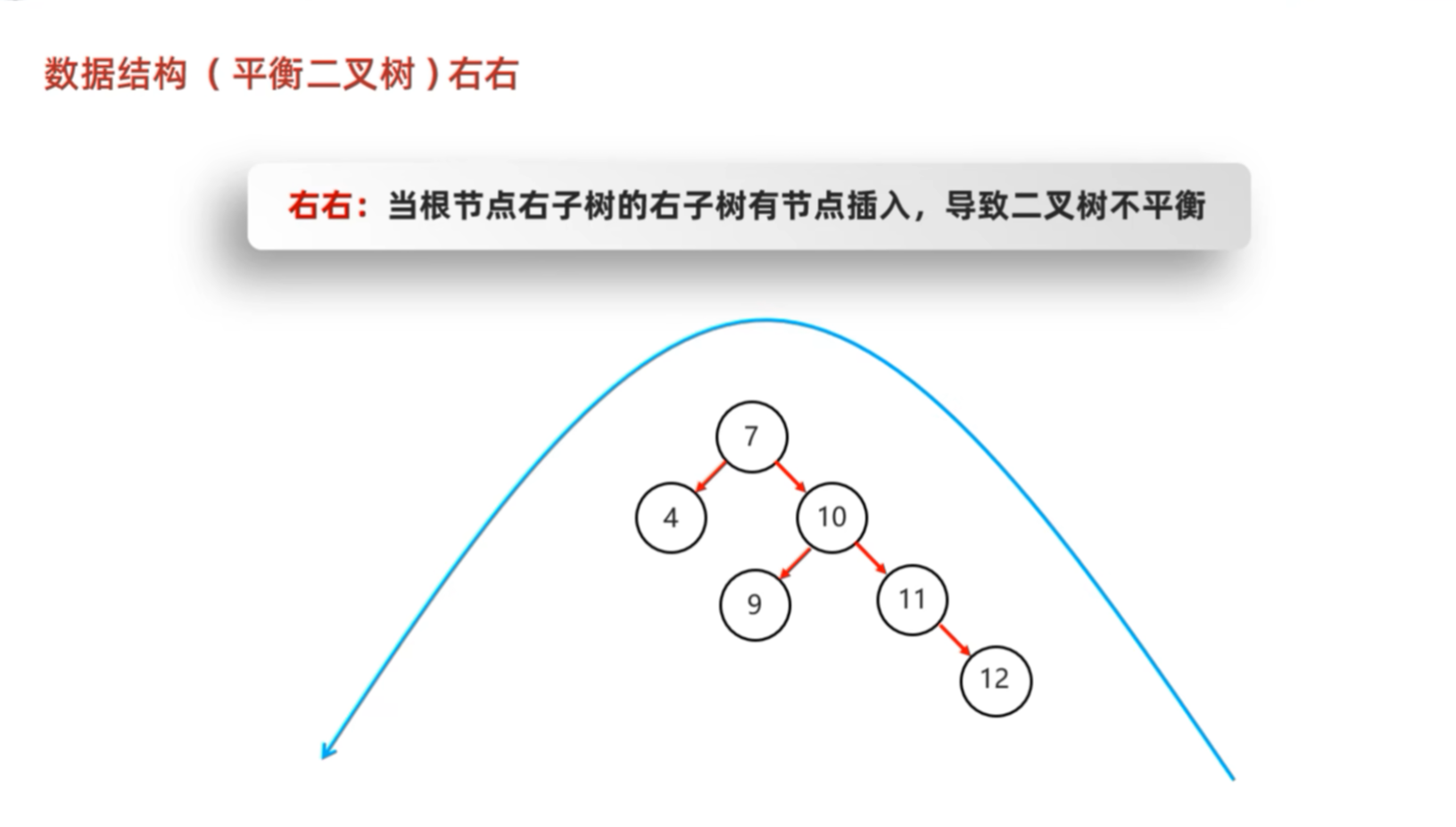
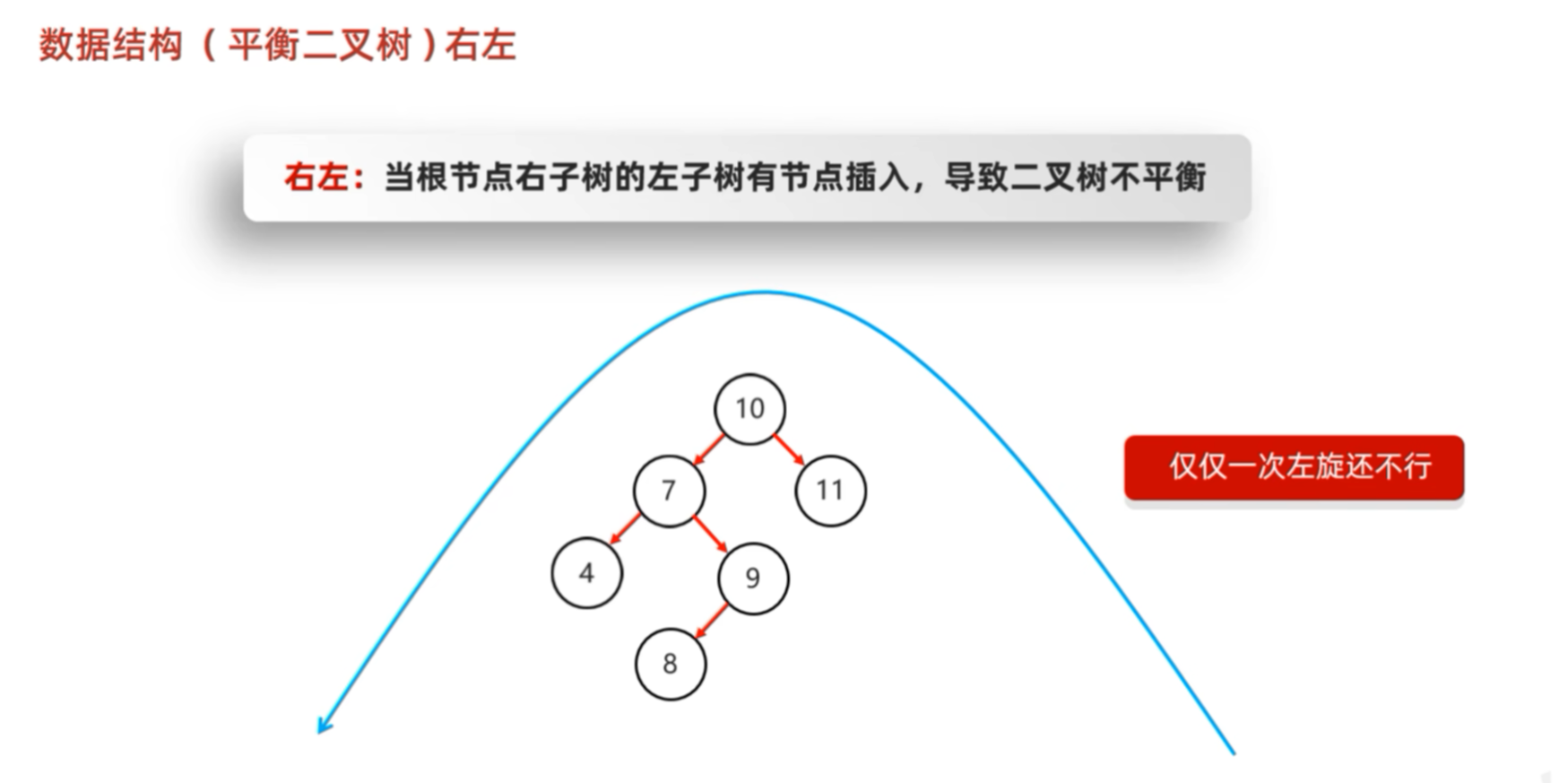
1.3 四种不平衡情况(必须掌握!)
当插入一个新节点后,从插入点向上回溯 ,第一个出现 |平衡因子| = 2 的节点就是"失衡点"。
根据新节点插入的位置,分为四种类型:
| 类型 | 名称 | 特征 | 解决方案 |
|---|---|---|---|
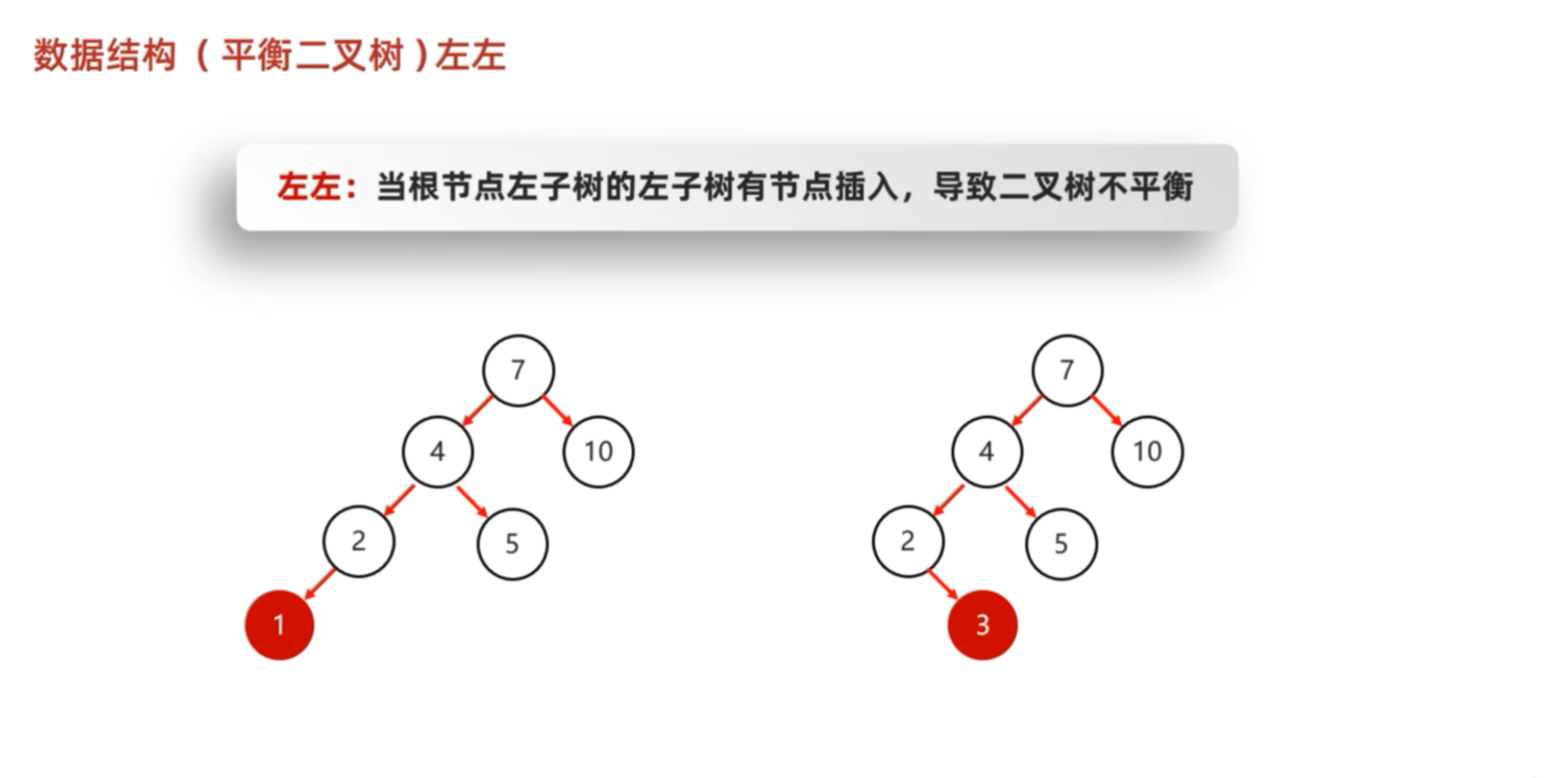
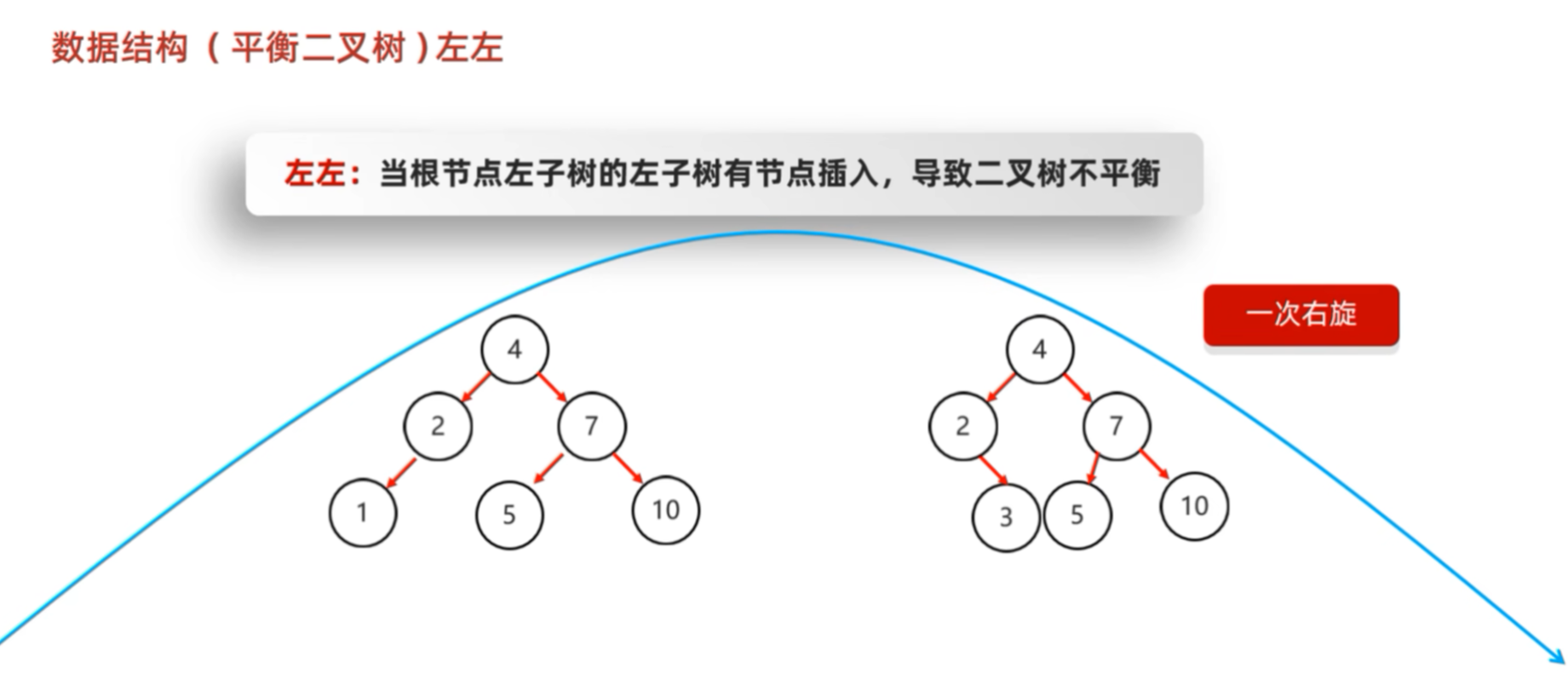
| LL | 左左 | 失衡节点的左孩子的左子树插入 | 右旋一次 |
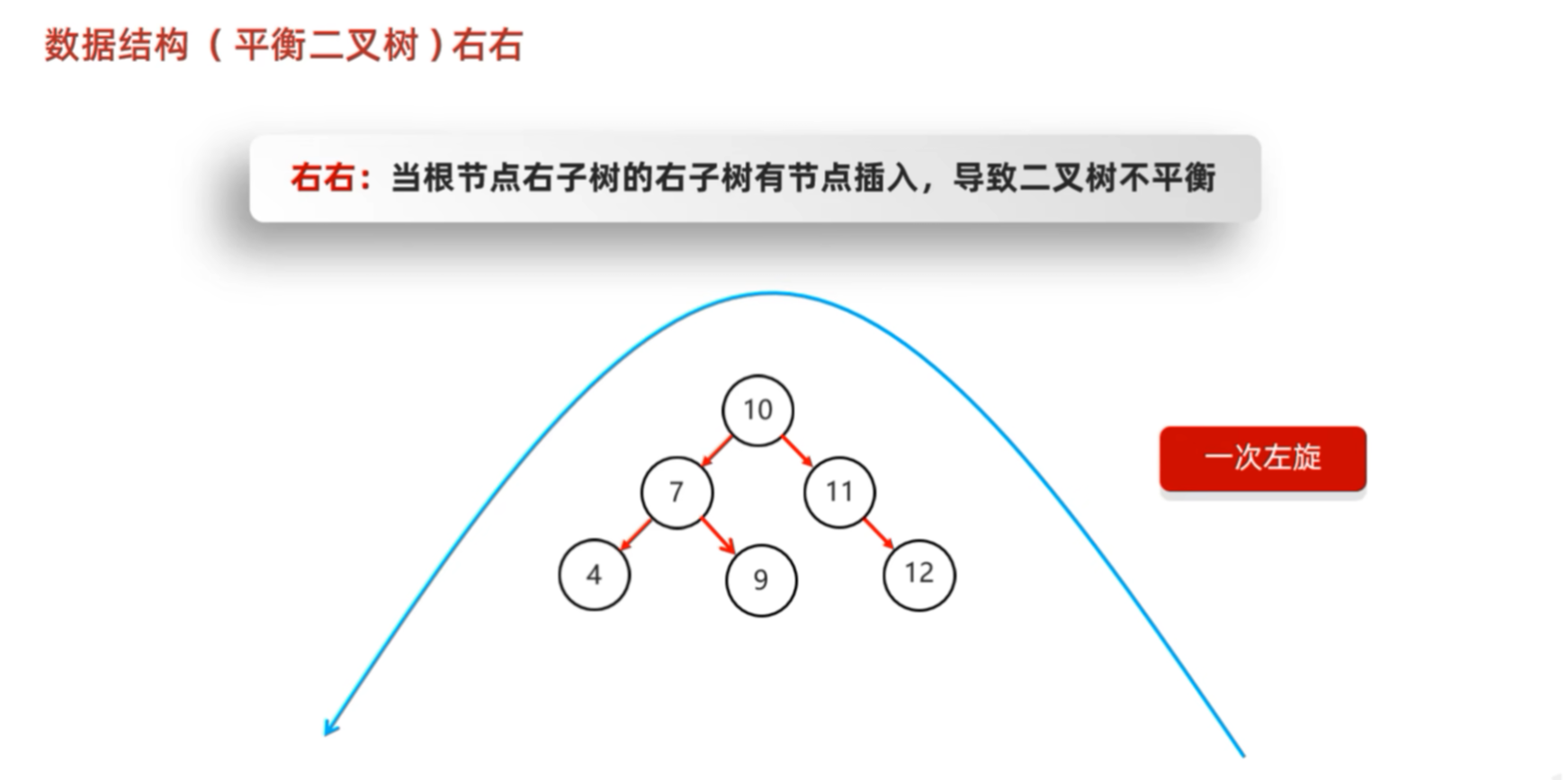
| RR | 右右 | 失衡节点的右孩子的右子树插入 | 左旋一次 |
| LR | 左右 | 失衡节点的左孩子的右子树插入 | 先左旋(对左孩子),再右旋(对失衡点) |
| RL | 右左 | 失衡节点的右孩子的左子树插入 | 先右旋(对右孩子),再左旋(对失衡点) |
✅ 记忆技巧:看最后两步路径方向 !
例如:从失衡点 → 左 → 右 → 就是 LR 型
这种情况,显然不平衡的节点是7,左子树树大于右边,进行右旋。
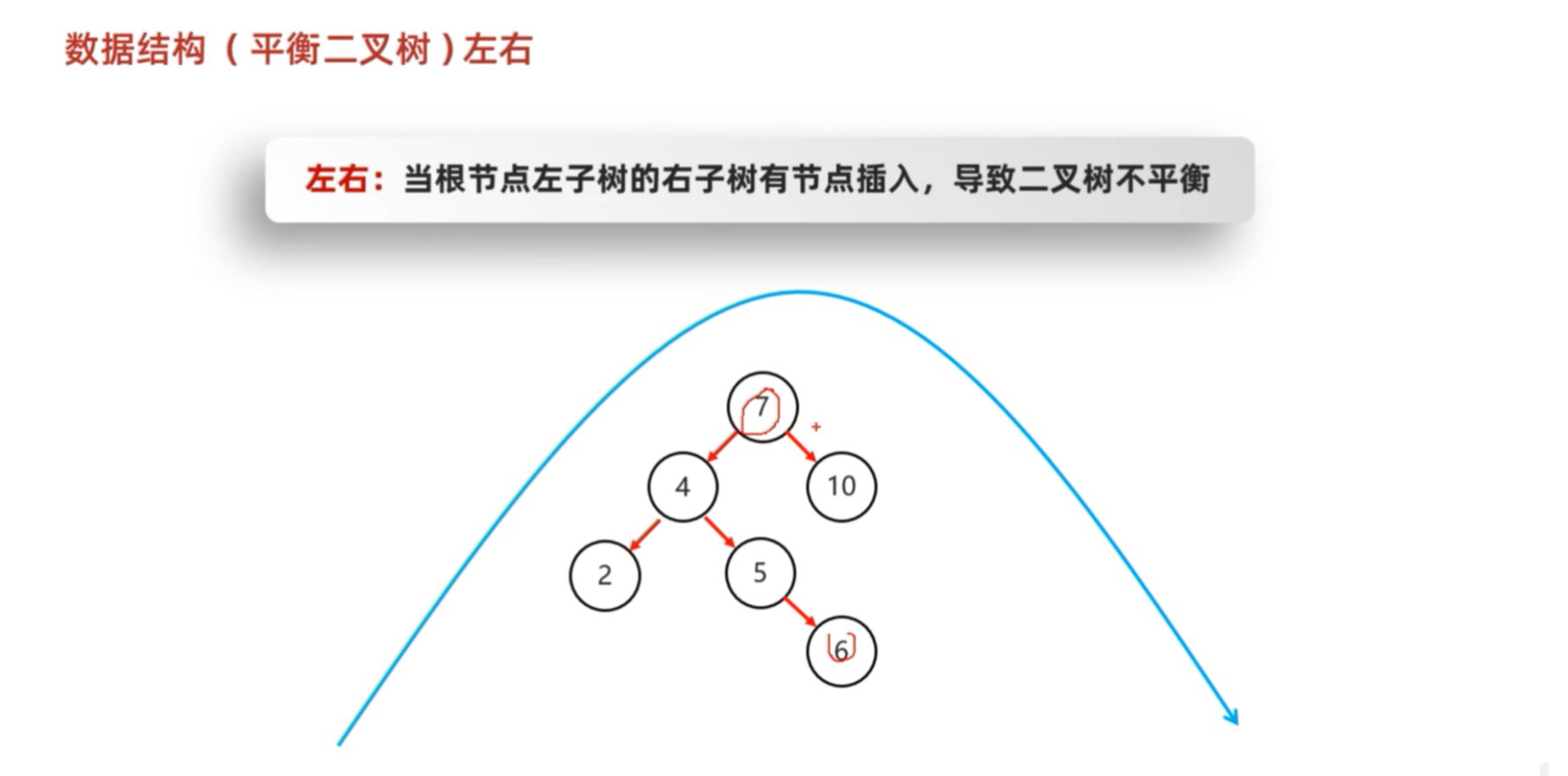
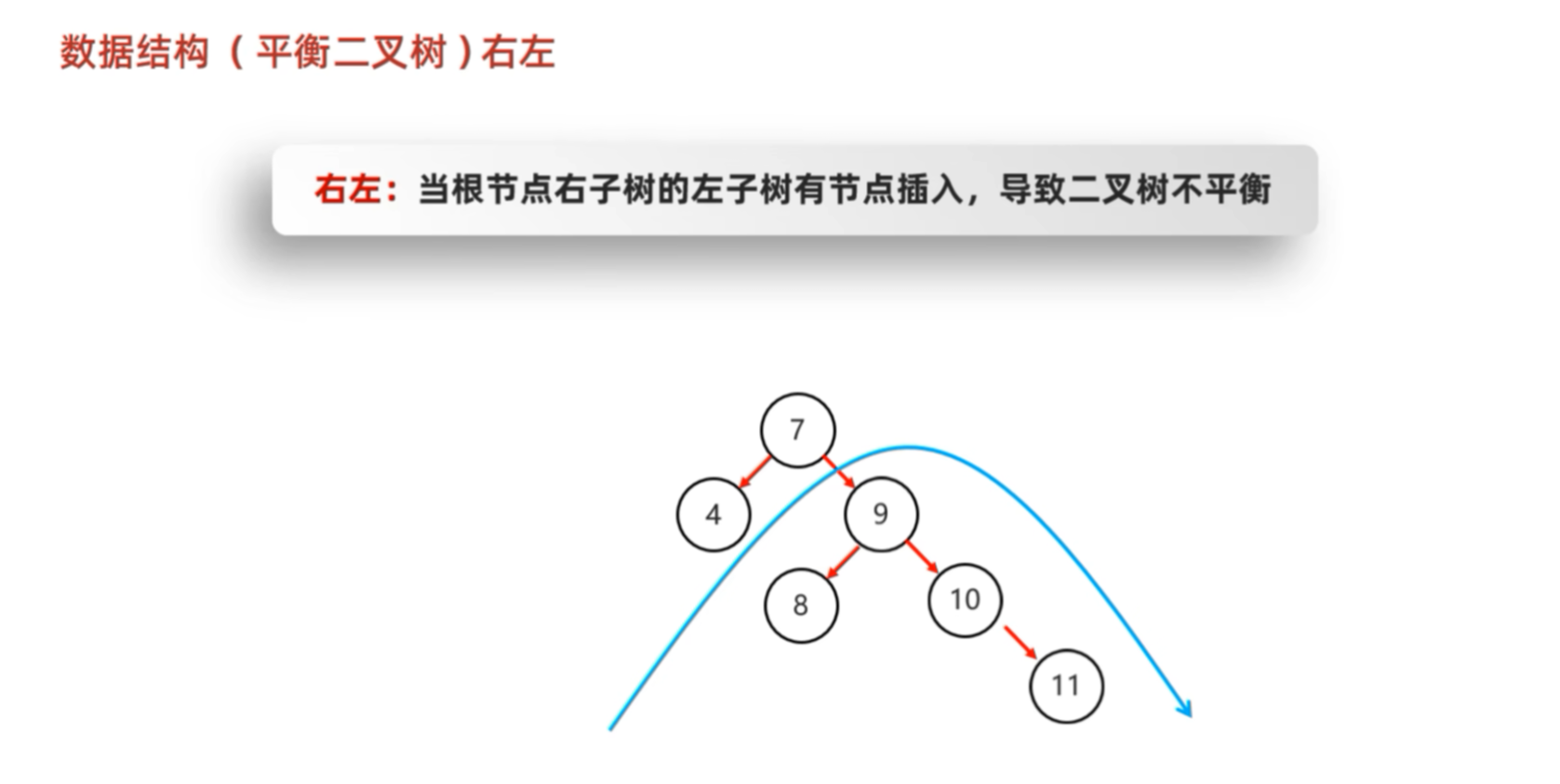
旋转之后:仍然不平衡
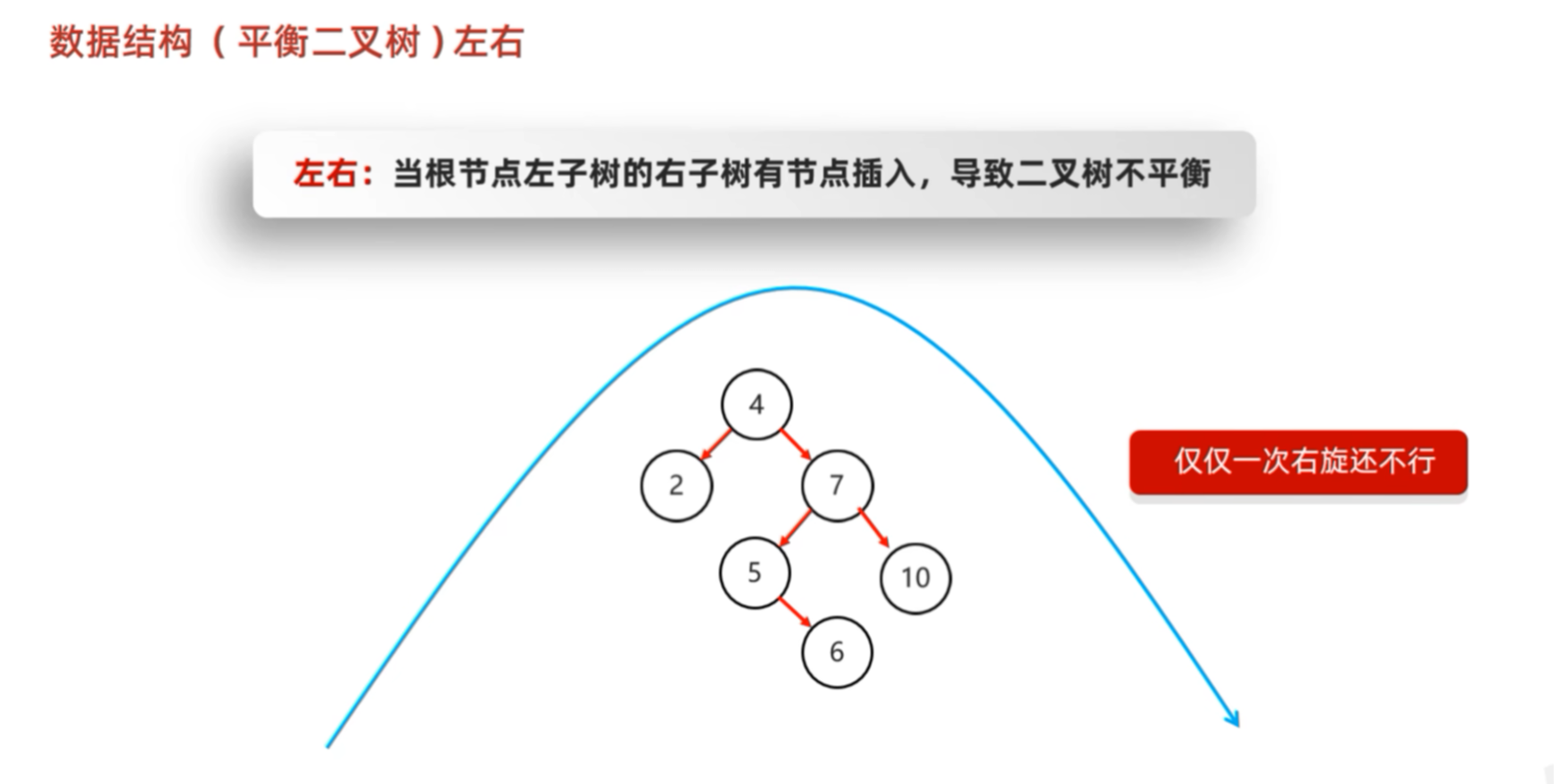
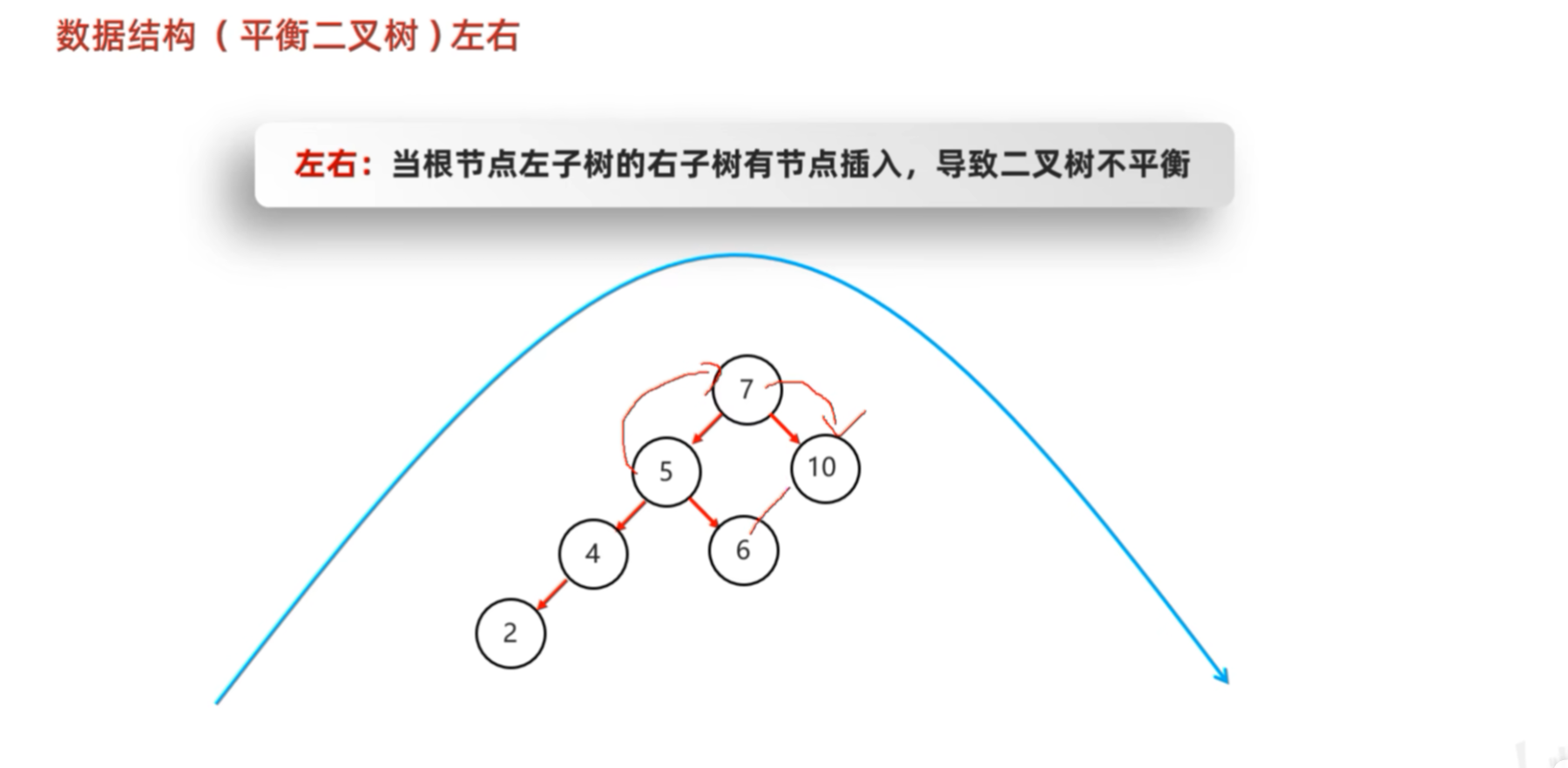
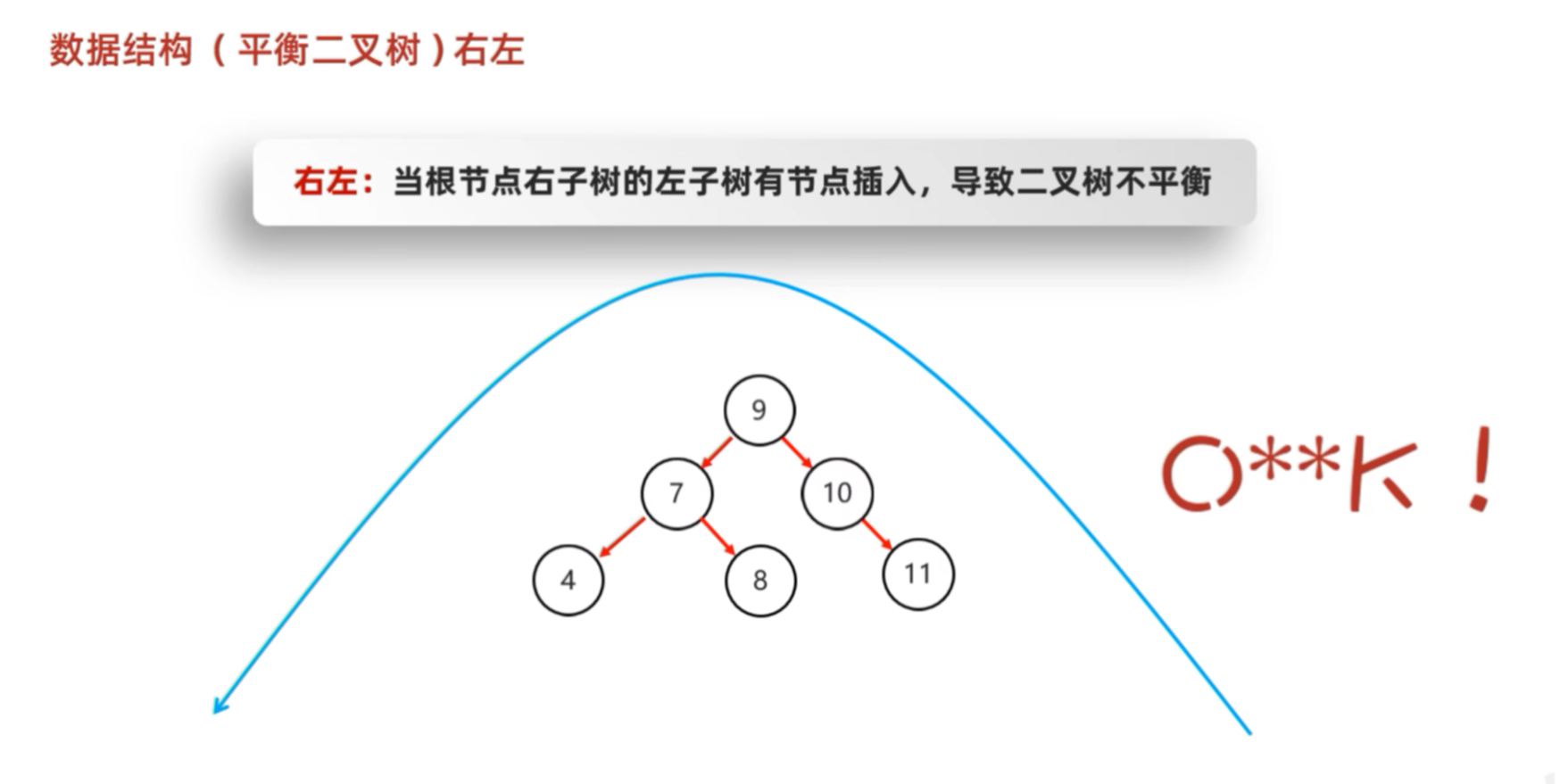
真正的解决方法为:先进行左旋,使其变成左左的情况,然后进行右旋。


1.4 平衡二叉树 vs 普通 BST 性能对比
| 操作 | 普通 BST(最坏) | AVL 树 |
|---|---|---|
| 查找 | O(n) | O(log n) |
| 插入 | O(n) | O(log n) |
| 删除 | O(n) | O(log n) |
| 空间开销 | 无额外 | 每个节点需存 height |
| 实现复杂度 | 简单 | 较复杂(需旋转) |
💡 AVL 适合查询多、插入少的场景;如果插入频繁,可考虑红黑树(允许轻微不平衡,旋转更少)
总结:关键要点
| 概念 | 说明 |
|---|---|
| 平衡因子 | 左子树高 - 右子树高,合法值:-1, 0, 1 |
| 左旋 | 解决"右重"问题,右孩子上位 |
| 右旋 | 解决"左重"问题,左孩子上位 |
| LL/RR | 单旋即可 |
| LR/RL | 双旋(先子后父) |
| 旋转原则 | 不破坏 BST 有序性,仅调整结构 |
| AVL 优势 | 严格平衡,查询极快 |
| AVL 劣势 | 插入/删除时旋转频繁,维护成本高 |
🌟 最后一句话总结 :
"平衡二叉树就像一棵会自我矫正的大树------无论你怎么'插',它都能通过'旋转'保持挺拔,确保每一片叶子都能被快速找到!"
声明:
题目详细分析借鉴于通义AI
以上均来源于B站@ITheima的教学内容!!!
本人跟着视频内容学习,整理知识引用