题目 D:树变链的最少操作数
题目描述
小芳有一颗 n 个节点的树,但小红更喜欢链。为了把这棵树变成链,小红可以进行如下操作:
选择任意一条边,其连接两个点 u, v。将这条边断开后,在点 u 所在连通块中任选一个节点,向点 v 连边。
小红想知道,要把这棵树变成链最少需要几次操作?
输入描述
第一行输入一个整数 n(1 ≤ n ≤ 2×10⁵)。之后的 n−1 行,每行输入两个整数 uᵢ, vᵢ(1 ≤ uᵢ, vᵢ ≤ n),代表有一条边连接 uᵢ 和 vᵢ。
输出描述
输出一个整数,代表小红所需的最少次数。
示例 1
输入
51 21 31 44 5
输出
1
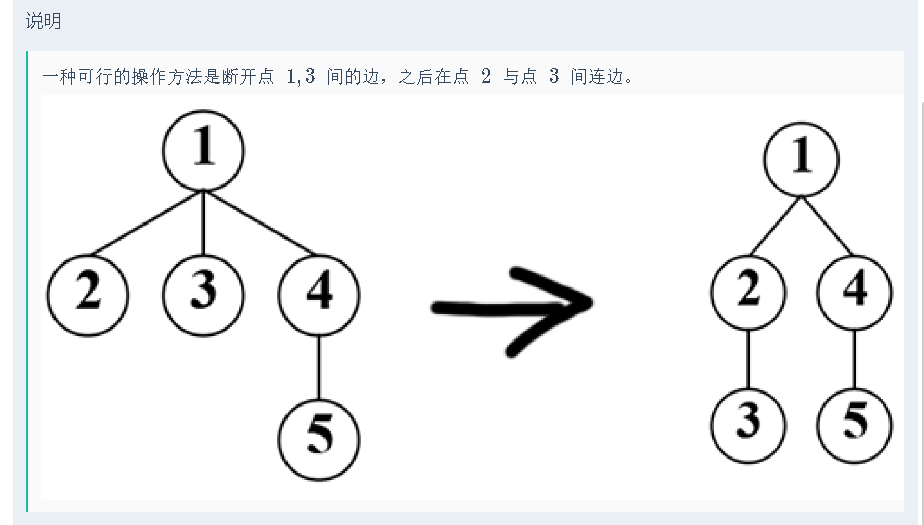
说明
一种可行的操作方法是断开点 1 和 3 间的边,之后在点 2 与点 3 间连边。
这道题我们可以先来考虑一下结果和初始状态有什么不同
先拿样例来说,最开始是最左边的树,经过操作变成了右边的链。
右边的链(但是看着有点像树)我们可以换个形式来看

这个样子看起来就好理解多了,那我们左图如何变成链呢?我们不难发现左图中1号点一定不是链中的点,为什么呢?
我们可以通过观察链的性质 :每个点的度不超过2,只在叶子结点度等于1。
所以我们可以想到需要去除1号点的某条边,使得能成为链中的点。
此时,我们可以想到答案的组成部分,把度大于2的点都存在起来if(deg>2):res+=(deg-2) res为答案,deg为度
那现在我们把deg大于2的部分都存起来了,该怎么接呢?
我们可以先把操作都存下来,不要着急操作,也就是把deg大于2的点存起来后不要着急接,因为我们最后的状态一定是一条链,我们无论是把deg大于2的点存下来后再去接,还是最后再去接都没有影响。这里可能有点抽象,我拿个样例演示一下
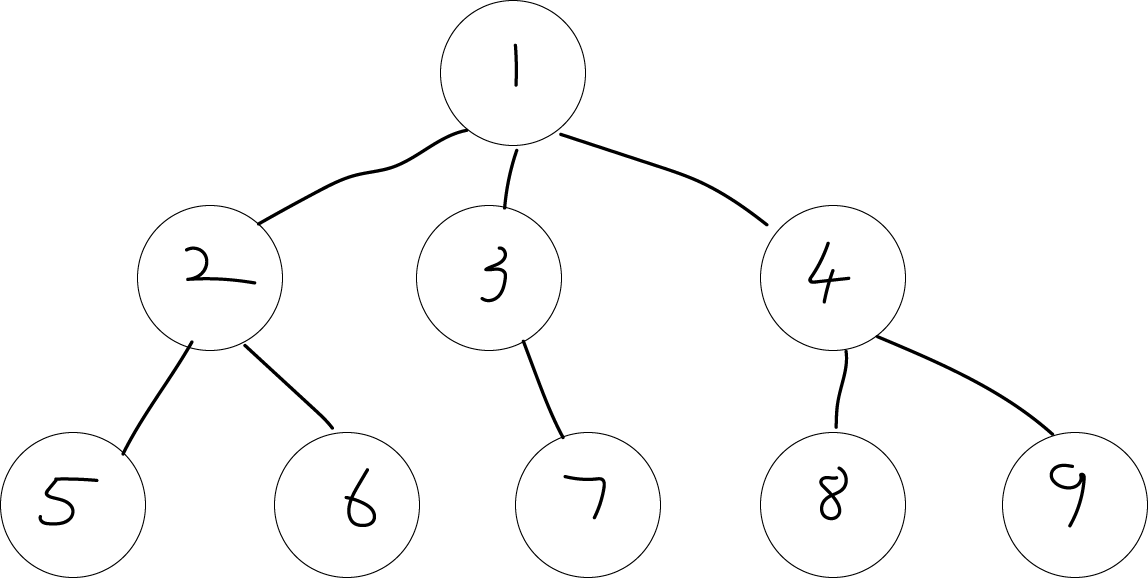
对于这颗树而言,度数大于2的点有:1,2,4,所以对于这三点,我们可以先拆连接1号点的某个边,存起来,此时有两种选择。
第一种选择,先存着,就像这样
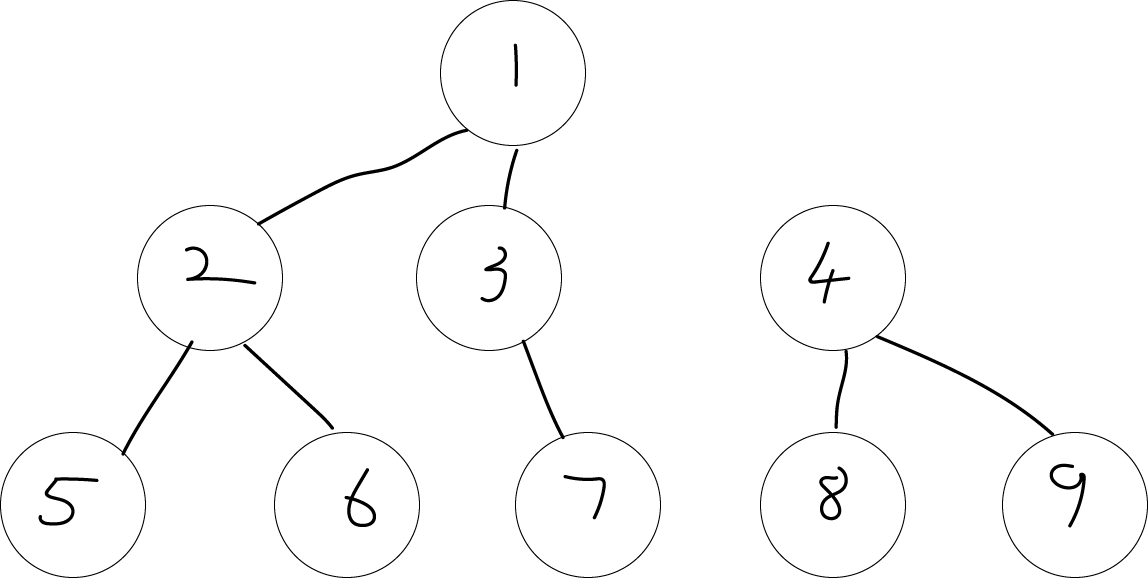
第二种选择,分开边后立即进行连接,连到某个节点上去
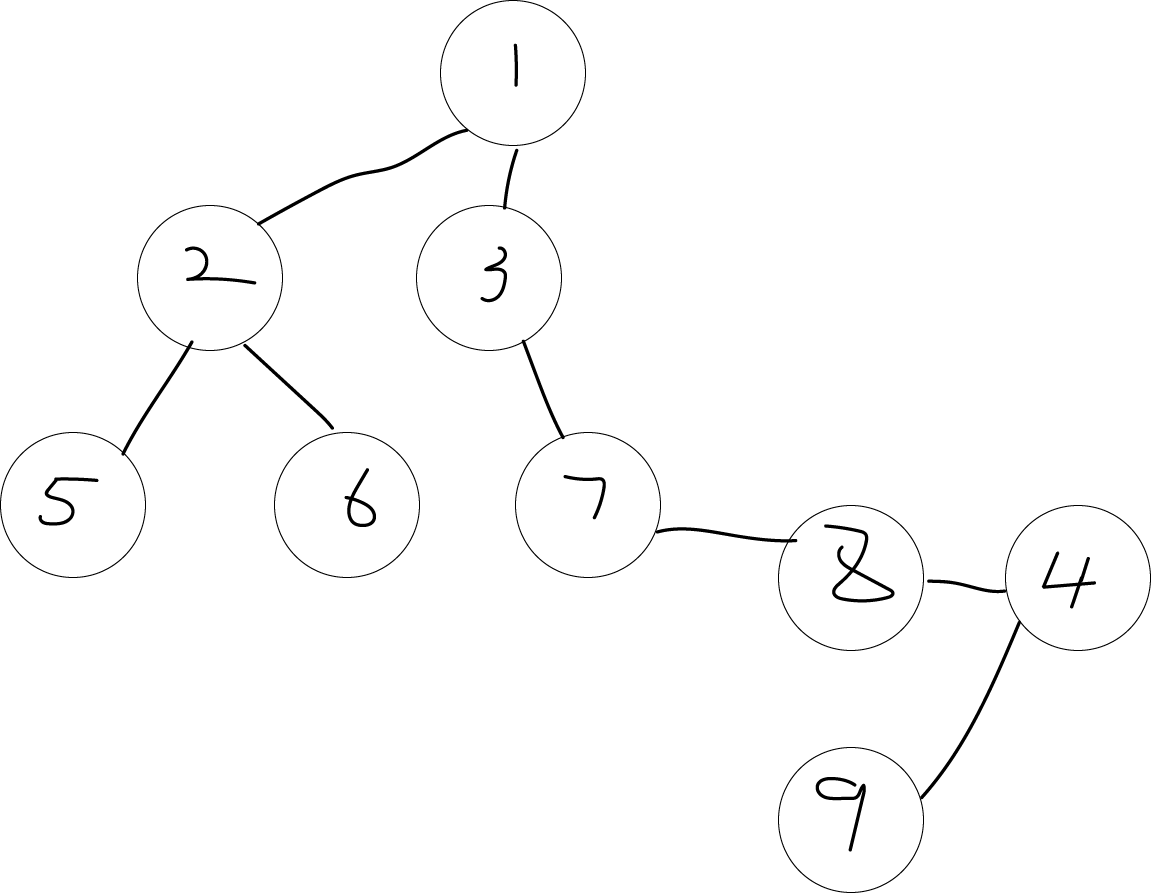
因为这道题没有要求我们给出操作顺序,所以无论哪种操作都是合法的,那我们就可以选一个省心一点的方式,把所有的边都拆完了,在进行组装。
我们把度大于2的部分都拆下来了,那原本的树就变成了什么了?是不是就变成了若干个链了?,因为我们此时每个点的度数都小于等于2完全就是合法的。
拿我们上面举的这颗树的例子,我们把所有度大于2的部分都拆下来
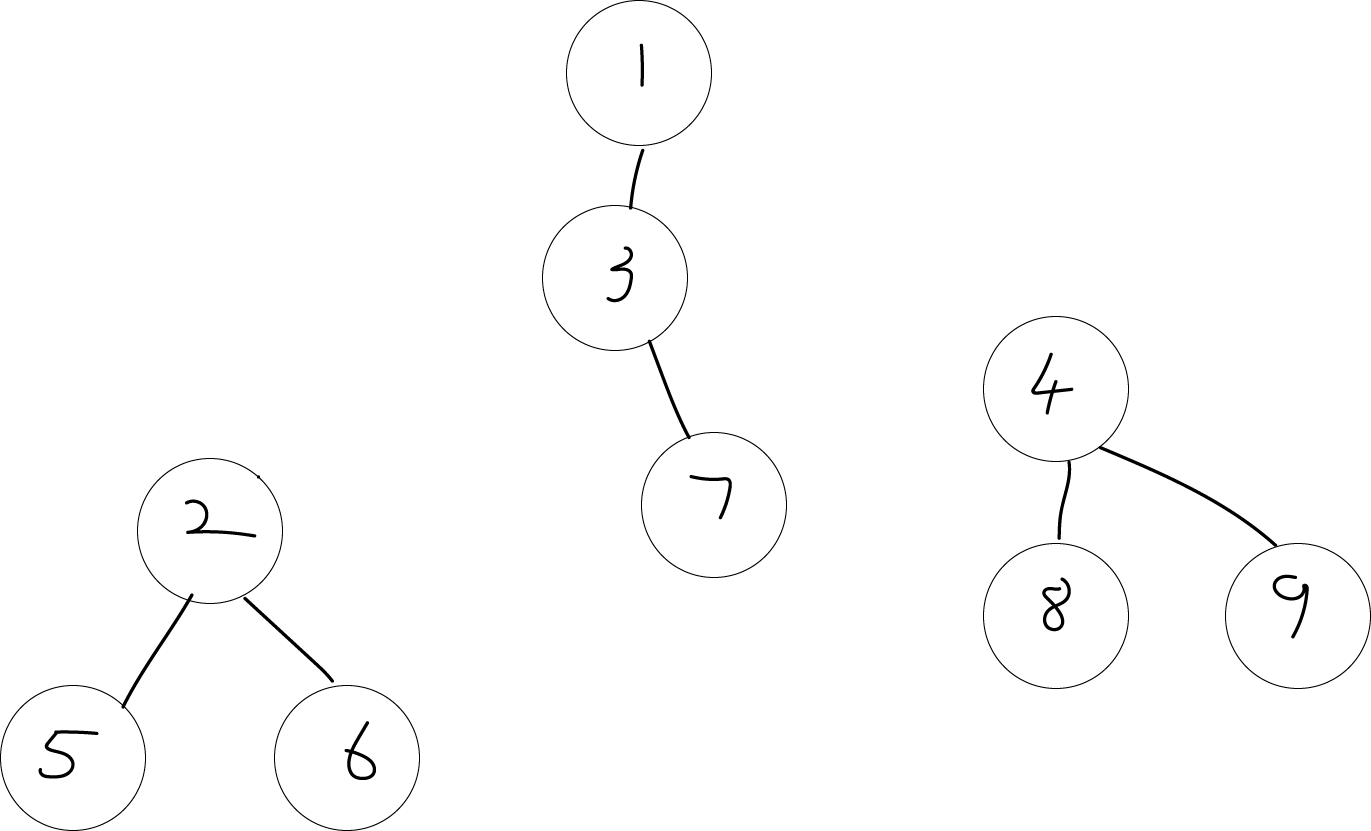
最后首尾相接一下不就变成了链了吗?
所以答案就是i从1到n遍历if(deg[i]>2):res+=(deg[i]-2)
代码奉上
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int deg[N],n;
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
long long res=0;
cin>>n;
for(int i=1;i<n;i++)
{
int u,v;
cin>>u>>v;
deg[u]++,deg[v]++;
}
for(int i=1;i<=n;i++){
res+=max(deg[i]-2,0);
}
cout<<res;
return 0;
}这道题其实教给我们两个点:
(1)当从开始状态推最终状态不好想时候,我们可以想想从最终状态到开始状态入手(正难则反)
(2)先把操作存下来,别急着进行操作