代码随想录 Q89.跳跃游戏Ⅱ

思路：这题比Q88.跳跃游戏要难，但是思路还是要看最大覆盖范围。本题要计算最少步数，因此要考虑什么时候步数加1。

1.贪心策略：以最少的步数增加覆盖范围，覆盖范围一旦覆盖到终点，得到的就是最少步数。

（1）局部最优：当前的可移动距离尽可能地多走（不能超过覆盖范围，并实时更新覆盖范围），如果还没到终点，步数加1。

（2）全局最优：一步尽可能地多走（不能超过覆盖范围，并实时更新覆盖范围），从而达到最少步数。

2.需要统计两个覆盖范围，当前这一步的最大覆盖和下一步的最大覆盖：如果移动下标达到当前这一步的最大覆盖的最远距离还没有到达终点的话，那就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。

如下图所示：

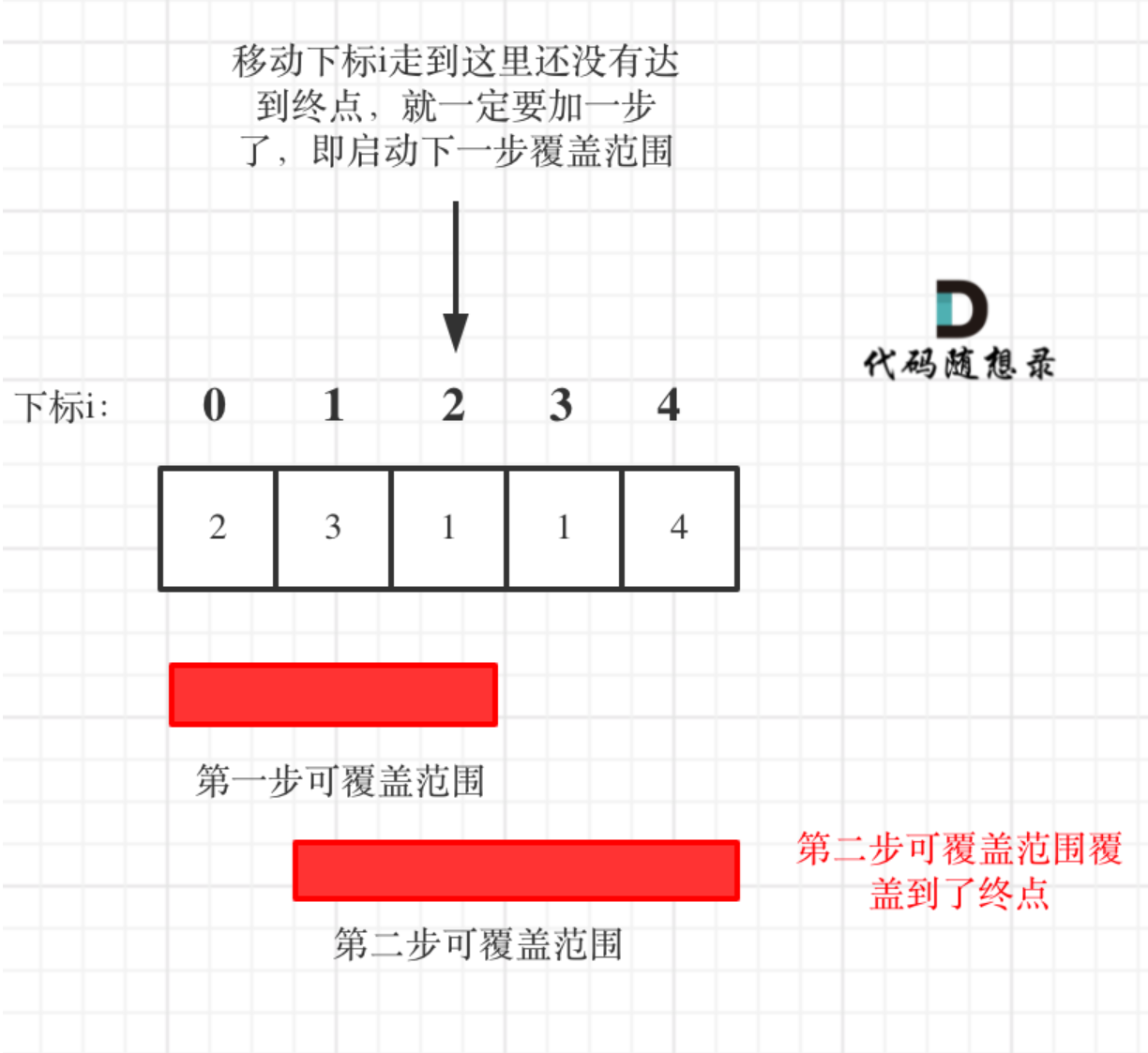
方法一：贪心。

（1）移动下标达到了当前覆盖的最远距离下标时，步数要加1，来增加覆盖距离。最后的步数就是最少步数。

（2）注意：当移动下标达到了当前覆盖的最远距离下标时：如果当前覆盖最远距离下标就是集合终点，那么步数就不用加1了，因为不能再往后走了。

附代码：

java 复制代码

class Solution {
    public int jump(int[] nums) {
        if(nums == null || nums.length == 0 || nums.length == 1){
            return 0;
        }
        // 记录跳跃的次数
        int count = 0;
        // 记录当前的覆盖最大范围
        int curdist = 0;
        // 记录下一步的最大覆盖范围
        int maxdist = 0;
        for(int i = 0;i < nums.length;i++){
            maxdist = Math.max(maxdist,i + nums[i]);
            // 说明当前一步再跳一步就到达了末尾
            if(maxdist >= nums.length - 1){
                count ++;
                break;
            }
            //走到当前可覆盖的最大范围时，更新下一步可达到的最大范围
            if(i == curdist){
                curdist = maxdist;
                count ++;
            }
        }
        return count;
    }
}

方法二：依然是贪心。

和方法一不同的是，移动下标只要遇到当前覆盖最远距离的下标，直接步数加1，不考虑是不是终点的情况。可达位置的改变次数就是跳跃次数。

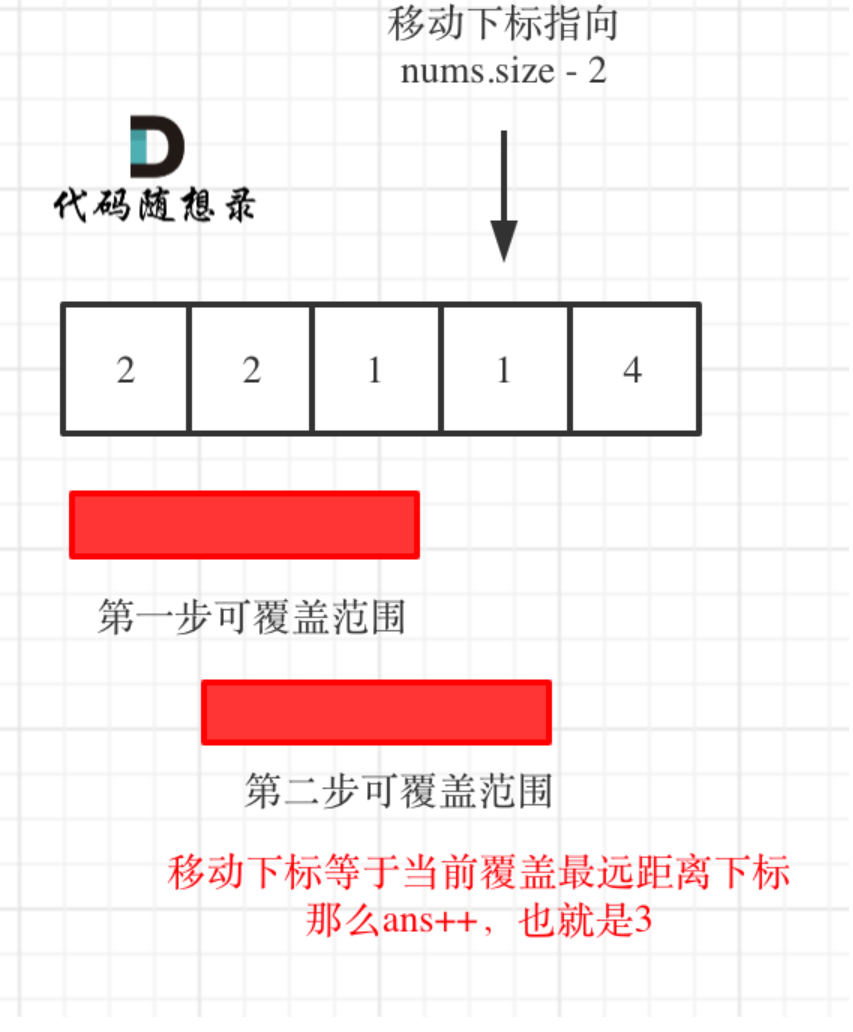
附代码：

java 复制代码

class Solution {
    public int jump(int[] nums) {
        int res = 0;
        //当前覆盖的最远距离下标
        int end = 0;
        //下一步覆盖的最远距离下标
        int temp = 0;
        for(int i = 0;i <= end && end < nums.length - 1;i ++){
            temp = Math.max(temp,i + nums[i]);
            //可达位置的改变次数就是跳跃次数
            if( i == end){
                end = temp;
                res ++;
            }
        }
        return res;
    }
}