目录
题目链接:
题目:
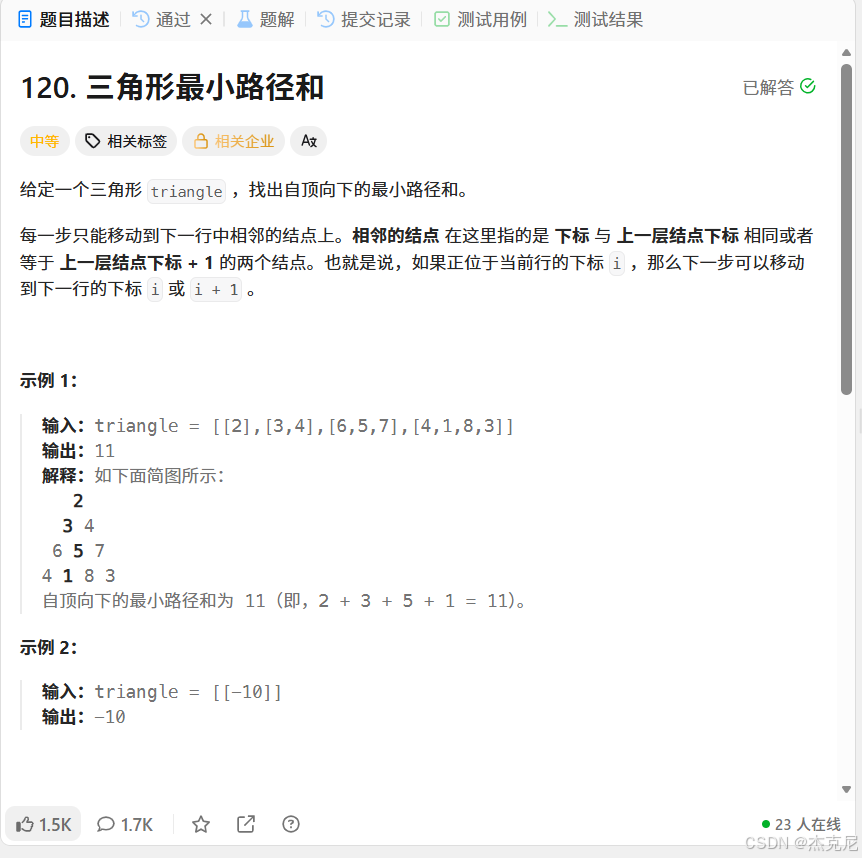
解题思路:
使用动态规划,最后看最后一行哪个最小就是目标结果
不能使用贪心算法,因为局部最优不等于全局最优
就比如说某一行 是1 和10要选择的,那么下一行万一1的下面俩是100000,而10下面是负数呢
所以不能使用贪心,只能使用动态规划将所有值都算出来
代码:
二维dp
java
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
// dp[i][j] 表示从顶部到第 i 行第 j 列的最小路径和
int[][] dp = new int[n][n];
// 初始化顶部节点
dp[0][0] = triangle.get(0).get(0);
for (int i = 1; i < n; i++) {
// 处理最左列:只能从正上方过来
dp[i][0] = dp[i-1][0] + triangle.get(i).get(0);
// 处理中间列:从左上方或正上方取最小值
for (int j = 1; j < i; j++) {
dp[i][j] = Math.min(dp[i-1][j-1], dp[i-1][j]) + triangle.get(i).get(j);
}
// 处理最右列:只能从左上方过来
dp[i][i] = dp[i-1][i-1] + triangle.get(i).get(i);
}
// 遍历最后一行,找最小值
int minTotal = dp[n-1][0];
for (int j = 1; j < n; j++) {
minTotal = Math.min(minTotal, dp[n-1][j]);
}
return minTotal;
}
}一维dp
java
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[] dp = new int[n];
dp[0] = triangle.get(0).get(0);
for (int i = 1; i < n; i++) {
// 先处理最右列(避免覆盖前一次的结果)
dp[i] = dp[i-1] + triangle.get(i).get(i);
// 处理中间列
for (int j = i-1; j > 0; j--) {
dp[j] = Math.min(dp[j-1], dp[j]) + triangle.get(i).get(j);
}
// 处理最左列
dp[0] += triangle.get(i).get(0);
}
int minTotal = dp[0];
for (int j = 1; j < n; j++) {
minTotal = Math.min(minTotal, dp[j]);
}
return minTotal;
}
}问题:
何时选择使用动态规划?
当一个问题具备最优子结构 和重叠子问题这两个核心特征时,就可以考虑使用动态规划(DP)来解决
何时二维dp能压缩成一维dp?
在动态规划(DP)中,将二维 DP 数组压缩为一维 DP 数组的核心依据是状态转移的依赖关系 。当二维 DP 的状态更新只依赖于上一行(或特定行)的状态,且不会发生 "覆盖冲突" 时,就可以通过复用一维数组来节省空间
总结:
深入解析三角形最小路径和问题的动态规划解法在算法领域,动态规划是解决具有最优子结构和重叠子问题特性问题的经典方法。LeetCode 上的 "三角形最小路径和" 问题(题目编号 120)就是动态规划的典型应用场景。本文将对该问题的动态规划解法代码进行全方位、超详细的解析,帮助读者深入理解动态规划的设计思路与实现细节。问题背景与分析"三角形最小路径和" 问题的描述是:给定一个三角形 triangle,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上(相邻的结点指的是下标与上一层结点下标相同或等于上一层结点下标 + 1 的两个结点)。例如,对于三角形 [[-1],[2,3],[1,-1,-3]],自顶向下的最小路径和为 -1 + 3 + (-3) = -1。要解决这个问题,我们需要找到一条从顶部到底部的路径,使得路径上所有数字之和最小。直接暴力枚举所有路径显然不可行,因为路径数量会随着三角形层数呈指数级增长。而动态规划通过利用子问题的最优解来构建原问题的最优解,能够将时间复杂度优化到可接受的范围。代码结构与核心思路我们来看这段解决该问题的 Java 代码:java运行class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int [][] dp = new int[n+1][n+1];
dp[0][0] = triangle.get(0).get(0);
for(int i=1;i<n;i++){
dp[i][0] = dp[i-1][0] + triangle.get(i).get(0);
for(int j=1;j<i;j++){
dp[i][j] = Math.min(dp[i-1][j-1], dp[i-1][j]) + triangle.get(i).get(j);
}
dp[i][i] = dp[i-1][i-1] + triangle.get(i).get(i);
}
int res = dp[n-1][0];
for(int i=1;i<triangle.get(n-1).size();i++){
res = Math.min(res, dp[n-1][i]);
}
return res;
}
}
这段代码的核心思路是使用二维动态规划数组 dp 来记录从顶部到三角形中每个位置的最小路径和。dp[i][j] 表示从三角形顶部(第 0 行第 0 列)到达第 i 行第 j 列的最小路径和。代码逐部分解析初始化部分java运行int n = triangle.size();
int [][] dp = new int[n+1][n+1];
dp[0][0] = triangle.get(0).get(0);
n = triangle.size();:首先获取三角形的层数 n。例如,对于三角形 [[-1],[2,3],[1,-1,-3]],n 的值为 3。int [][] dp = new int[n+1][n+1];:创建一个 (n+1) x (n+1) 的二维数组 dp。这里使用 n+1 的维度是为了方便处理边界条件,避免数组越界的判断。dp[0][0] = triangle.get(0).get(0);:初始化三角形顶部的最小路径和,即第 0 行第 0 列的最小路径和就是其自身的值。状态转移循环java运行for(int i=1;i<n;i++){
dp[i][0] = dp[i-1][0] + triangle.get(i).get(0);
for(int j=1;j<i;j++){
dp[i][j] = Math.min(dp[i-1][j-1], dp[i-1][j]) + triangle.get(i).get(j);
}
dp[i][i] = dp[i-1][i-1] + triangle.get(i).get(i);
}
这部分是动态规划的核心 ------状态转移过程。我们逐行计算每个位置的最小路径和:处理每一行的第一个元素(最左列)java运行dp[i][0] = dp[i-1][0] + triangle.get(i).get(0);
对于第 i 行第 0 列的元素,它只能从其正上方的元素(第 i-1 行第 0 列)移动而来。因此,其最小路径和等于正上方元素的最小路径和加上当前元素的值。处理每一行的中间元素java运行for(int j=1;j<i;j++){
dp[i][j] = Math.min(dp[i-1][j-1], dp[i-1][j]) + triangle.get(i).get(j);
}
对于第 i 行第 j 列(0 < j < i)的中间元素,它可以从两个方向移动而来:左上方:第 i-1 行第 j-1 列正上方:第 i-1 行第 j 列因此,我们需要取这两个方向的最小路径和,再加上当前元素的值,作为当前位置的最小路径和。处理每一行的最后一个元素(最右列)java运行dp[i][i] = dp[i-1][i-1] + triangle.get(i).get(i);
对于第 i 行第 i 列的元素,它只能从其左上方的元素(第 i-1 行第 i-1 列)移动而来。因此,其最小路径和等于左上方元素的最小路径和加上当前元素的值。结果计算java运行int res = dp[n-1][0];
for(int i=1;i<triangle.get(n-1).size();i++){
res = Math.min(res, dp[n-1][i]);
}
return res;
当我们计算完所有位置的最小路径和后,需要找出最后一行(第 n-1 行)中所有位置的最小路径和,这个最小值就是整个三角形的最小路径和。动态规划的时间与空间复杂度分析时间复杂度代码中的主要操作是两层循环:外层循环遍历三角形的每一行,共 n-1 次(从第 1 行到第 n-1 行)。内层循环在每一行中遍历从第 1 列到第 i-1 列的元素。总的时间复杂度为 \(O(n^2)\),其中 n 是三角形的层数。这相对于暴力枚举的指数级时间复杂度来说,是一个巨大的优化。空间复杂度代码中使用了一个 (n+1) x (n+1) 的二维数组 dp,因此空间复杂度为 \(O(n^2)\)。优化思路:空间复杂度优化当前代码的空间复杂度为 \(O(n^2)\),我们可以对其进行优化,将空间复杂度降低到 \(O(n)\)。观察状态转移方程可以发现,计算第 i 行的 dp 值时,只需要第 i-1 行的 dp 值。因此,我们可以使用一个一维数组来滚动更新。优化后的代码如下:java运行class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[] dp = new int[n];
dp[0] = triangle.get(0).get(0);
for (int i = 1; i < n; i++) {
// 先处理最后一个元素,避免覆盖
dp[i] = dp[i-1] + triangle.get(i).get(i);
for (int j = i-1; j > 0; j--) {
dp[j] = Math.min(dp[j-1], dp[j]) + triangle.get(i).get(j);
}
dp[0] += triangle.get(i).get(0);
}
int res = dp[0];
for (int i = 1; i < n; i++) {
res = Math.min(res, dp[i]);
}
return res;
}
}
在优化后的代码中,我们使用一维数组 dp,其长度为 n。在计算第 i 行时,我们从右向左更新 dp 数组,以避免覆盖还需要使用的上一行的 dp 值。优化后的空间复杂度为 \(O(n)\),时间复杂度仍为 \(O(n^2)\)。动态规划的解题步骤总结通过对 "三角形最小路径和" 问题的动态规划解法分析,我们可以总结出动态规划问题的一般解题步骤:定义状态:明确 dp[i][j](或 dp[i])所代表的具体含义。在本题中,dp[i][j] 表示从顶部到第 i 行第 j 列的最小路径和。确定状态转移方程:根据问题的逻辑关系,推导出当前状态与子状态之间的转移关系。本题的状态转移方程分为三种情况:最左列、中间列和最右列。初始化状态:确定动态规划数组的初始值,通常是问题的边界情况。本题中,dp[0][0] 的初始值就是三角形顶部元素的值。遍历计算所有状态:按照状态转移方程,依次计算出所有需要的状态值。返回结果:根据问题的要求,从所有计算得到的状态值中找到最终的答案。本题中,最终的答案是最后一行所有 dp 值中的最小值。总结"三角形最小路径和" 问题是动态规划的经典应用,通过定义合理的状态和状态转移方程,我们能够高效地解决这个问题。本文详细解析了该问题的动态规划解法代码,包括状态定义、状态转移、初始化、结果计算等各个环节,并分析了算法的时间和空间复杂度,最后还给出了空间复杂度的优化思路。动态规划的核心思想是 "用空间换时间",通过存储子问题的解来避免重复计算。掌握动态规划的关键在于准确识别问题的最优子结构和重叠子问题,并能够正确地定义状态和推导状态转移方程。希望通过本文的解析,读者能够对动态规划有更深入的理解,并能够将其应用到更多类似的算法问题中。