CUDA学习5-矩阵乘法（共享内存版）

wanzhong23332025-12-27 22:02

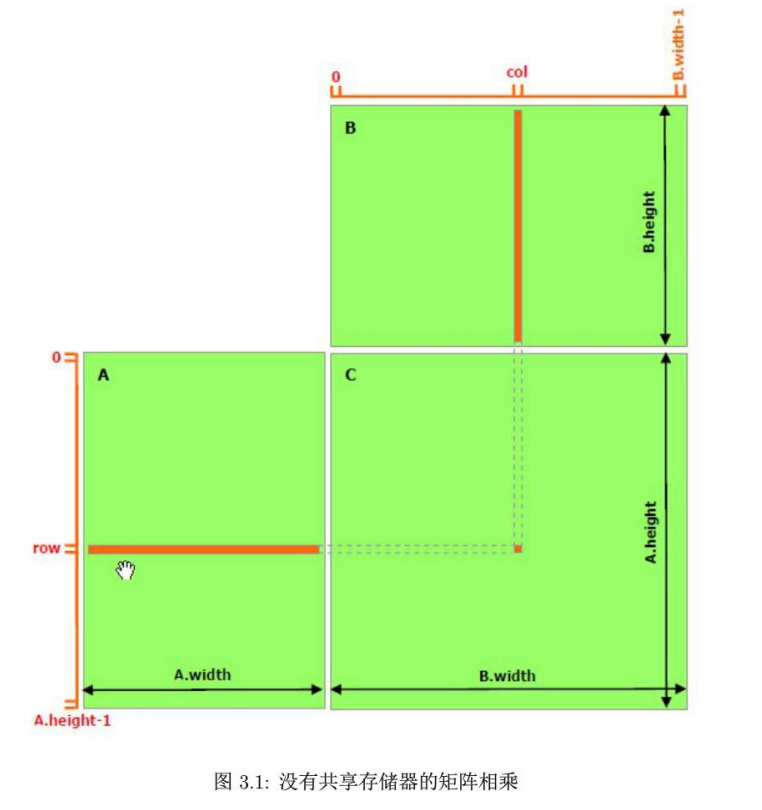
普通矩阵乘法

在未使用共享存储器（Shared Memory）时，CUDA 矩阵乘法的计算逻辑 是在 SM（流多处理器）的 CUDA Core 中执行的，临时数据会优先存在寄存器（Register） 中；但 A、B 矩阵的读取、C 矩阵的写入 完全依赖全局存储器（Global Memory）

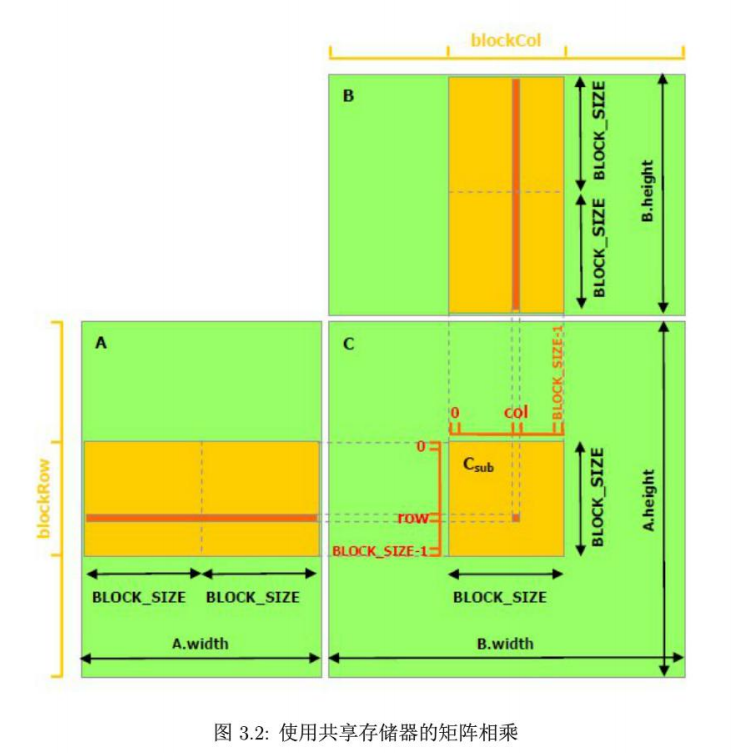
共享存储的矩阵乘法

使用共享存储器的时候

完整代码

vscode配置好环境之后（不会的看我往期博文），可以直接将代码粘贴到.cu文件中编译运行。代码的细节以及相关内容讲解放在完整代码的后面，诸君稍安勿躁。

cpp 复制代码 
nvcc mul_share.cu -o mul_share
cpp 复制代码 
// mul_share.cu


#include <iostream>
#include <cuda_runtime.h>
#include <cmath>
#include <chrono>
#include <iomanip>
#include <vector>
#include <tuple>
#include <cstdlib>

#define BLOCK_SIZE 16
#define CHECK(call) \
    do { \
        cudaError_t err = call; \
        if (err != cudaSuccess) { \
            std::cerr << "CUDA Error: " << cudaGetErrorString(err) \
                      << " at line " << __LINE__ << std::endl; \
            exit(EXIT_FAILURE); \
        } \
    } while (0)

typedef struct {
    int width;
    int height;
    int stride; 
    float *elements;
} Matrix;

__device__ float getElement(const Matrix &mat, int row, int col) { 
    return mat.elements[row * mat.stride + col];
}


__device__ void setElement(Matrix &mat, int row, int col, float value) {
    mat.elements[row * mat.stride + col] = value;
}


__global__ void matrixMulSharedKernel(const Matrix A, const Matrix B, Matrix C) {
    // Shared memory declaration
    __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];
    
    // Thread indices
    int bx = blockIdx.x;
    int by = blockIdx.y;
    int tx = threadIdx.x;
    int ty = threadIdx.y;
    
    int row = by * BLOCK_SIZE + ty;
    int col = bx * BLOCK_SIZE + tx;
    
    float Cvalue = 0.0f;
    
    for (int m = 0; m < (A.width + BLOCK_SIZE - 1) / BLOCK_SIZE; ++m) { // (A.width + BLOCK_SIZE - 1) / BLOCK_SIZE是A.width/BLOCK_SIZE向上取整的标准写法，适用所有未知情况。
        // Load A tile into shared memory
        if (row < A.height && (m * BLOCK_SIZE + tx) < A.width) {
            As[ty][tx] = getElement(A, row, m * BLOCK_SIZE + tx);
        } else {
            As[ty][tx] = 0.0f;
        }
        
        if ((m * BLOCK_SIZE + ty) < B.height && col < B.width) {
            Bs[ty][tx] = getElement(B, m * BLOCK_SIZE + ty, col);
        } else {
            Bs[ty][tx] = 0.0f;
        }
        
        __syncthreads();
        
        for (int k = 0; k < BLOCK_SIZE; ++k) {
            Cvalue += As[ty][k] * Bs[k][tx];
        }
        
        __syncthreads();
    }
    
    if (row < C.height && col < C.width) {
        setElement(C, row, col, Cvalue);
    }
}

void matrixMulCPU(const Matrix &A, const Matrix &B, Matrix &C) {
    for (int i = 0; i < C.height; ++i) {
        for (int j = 0; j < C.width; ++j) {
            float sum = 0.0f;
            for (int k = 0; k < A.width; ++k) {
                sum += A.elements[i * A.stride + k] * B.elements[k * B.stride + j];
            }
            C.elements[i * C.stride + j] = sum;
        }
    }
}

void initMatrix(Matrix &mat, bool random = true) {
    // Use fixed seed for reproducibility
    if (random) {
        srand(42);  // Fixed seed
    }
    
    for (int i = 0; i < mat.height; ++i) {
        for (int j = 0; j < mat.width; ++j) {
            if (random) {
                // Generate values in smaller range to reduce accumulation error
                mat.elements[i * mat.stride + j] = static_cast<float>(rand() % 10) / 10.0f;
            } else {
                mat.elements[i * mat.stride + j] = 0.0f;
            }
        }
    }
}

// Compare two matrices (using relative error)
bool compareMatrices(const Matrix &A, const Matrix &B, float relativeEpsilon = 1e-5, float absoluteEpsilon = 1e-5) {
    if (A.height != B.height || A.width != B.width) {
        std::cout << "Matrix dimensions mismatch!" << std::endl;
        return false;
    }
    
    int totalElements = A.height * A.width;
    int mismatches = 0;
    float maxRelativeError = 0.0f;
    
    for (int i = 0; i < A.height; ++i) {
        for (int j = 0; j < A.width; ++j) {
            float a = A.elements[i * A.stride + j];
            float b = B.elements[i * B.stride + j];
            float diff = fabs(a - b);
            
            // Calculate relative error
            float relativeError = 0.0f;
            if (fabs(a) > absoluteEpsilon || fabs(b) > absoluteEpsilon) {
                relativeError = diff / std::max(fabs(a), fabs(b));
            }
            
            if (relativeError > maxRelativeError) {
                maxRelativeError = relativeError;
            }
            
            // If both absolute and relative errors exceed thresholds, consider it an error
            if (diff > absoluteEpsilon && relativeError > relativeEpsilon) {
                if (mismatches < 5) {  // Print only first few errors
                    std::cout << std::fixed << std::setprecision(15);
                    std::cout << "Mismatch at (" << i << ", " << j << "): "
                              << a << " vs " << b 
                              << ", diff=" << diff 
                              << ", rel_err=" << relativeError << std::endl;
                }
                mismatches++;
                if (mismatches > 100) {  // Stop if too many errors
                    std::cout << "Too many mismatches, stopping comparison..." << std::endl;
                    return false;
                }
            }
        }
    }
    
    if (mismatches > 0) {
        std::cout << "Total mismatches: " << mismatches << "/" << totalElements 
                  << ", Max relative error: " << maxRelativeError << std::endl;
        return false;
    }
    
    std::cout << "Matrices match with max relative error: " << maxRelativeError << std::endl;
    return true;
}

// Validate matrix multiplication for a given size
void validateMatrixMul(int M, int N, int K) {
    std::cout << "\n=== Matrix Multiplication Validation ===" << std::endl;
    std::cout << "Matrix dimensions: A(" << M << "x" << N << ") * B(" 
              << N << "x" << K << ") = C(" << M << "x" << K << ")" << std::endl;
    
    // Allocate memory on host
    Matrix h_A, h_B, h_C_cpu, h_C_gpu;
    
    h_A.height = M;
    h_A.width = N;
    h_A.stride = N;
    h_A.elements = new float[M * N];
    
    h_B.height = N;
    h_B.width = K;
    h_B.stride = K;
    h_B.elements = new float[N * K];
    
    h_C_cpu.height = M;
    h_C_cpu.width = K;
    h_C_cpu.stride = K;
    h_C_cpu.elements = new float[M * K];
    
    h_C_gpu.height = M;
    h_C_gpu.width = K;
    h_C_gpu.stride = K;
    h_C_gpu.elements = new float[M * K];
    
    // Initialize matrices
    std::cout << "Initializing matrices..." << std::endl;
    initMatrix(h_A, true);
    initMatrix(h_B, true);
    
    // Initialize C matrices to 0
    for (int i = 0; i < M * K; i++) {
        h_C_cpu.elements[i] = 0.0f;
        h_C_gpu.elements[i] = 0.0f;
    }
    
    // Allocate memory on device
    Matrix d_A, d_B, d_C;
    
    d_A.height = M;
    d_A.width = N;
    d_A.stride = N;
    CHECK(cudaMalloc(&d_A.elements, M * N * sizeof(float)));
    
    d_B.height = N;
    d_B.width = K;
    d_B.stride = K;
    CHECK(cudaMalloc(&d_B.elements, N * K * sizeof(float)));
    
    d_C.height = M;
    d_C.width = K;
    d_C.stride = K;
    CHECK(cudaMalloc(&d_C.elements, M * K * sizeof(float)));
    
    // Copy data from host to device
    std::cout << "Copying data to GPU..." << std::endl;
    CHECK(cudaMemcpy(d_A.elements, h_A.elements, M * N * sizeof(float), 
                     cudaMemcpyHostToDevice));
    CHECK(cudaMemcpy(d_B.elements, h_B.elements, N * K * sizeof(float), 
                     cudaMemcpyHostToDevice));
    CHECK(cudaMemset(d_C.elements, 0, M * K * sizeof(float)));
    
    // Set CUDA kernel parameters
    dim3 blockSize(BLOCK_SIZE, BLOCK_SIZE);
    dim3 gridSize((K + BLOCK_SIZE - 1) / BLOCK_SIZE, 
                  (M + BLOCK_SIZE - 1) / BLOCK_SIZE);
    
    std::cout << "Launching CUDA kernel..." << std::endl;
    std::cout << "Grid size: (" << gridSize.x << ", " << gridSize.y << ")" << std::endl;
    std::cout << "Block size: (" << blockSize.x << ", " << blockSize.y << ")" << std::endl;
    
    // Run GPU version and time it
    auto start_gpu = std::chrono::high_resolution_clock::now();
    
    matrixMulSharedKernel<<<gridSize, blockSize>>>(d_A, d_B, d_C);
    
    CHECK(cudaDeviceSynchronize());
    auto end_gpu = std::chrono::high_resolution_clock::now();
    
    // Check for kernel execution errors
    cudaError_t kernelError = cudaGetLastError();
    if (kernelError != cudaSuccess) {
        std::cerr << "Kernel launch failed: " << cudaGetErrorString(kernelError) << std::endl;
        exit(EXIT_FAILURE);
    }
    
    // Copy results back from device to host
    std::cout << "Copying results back to CPU..." << std::endl;
    CHECK(cudaMemcpy(h_C_gpu.elements, d_C.elements, M * K * sizeof(float), 
                     cudaMemcpyDeviceToHost));
    
    // Run CPU version and time it
    std::cout << "Running CPU version..." << std::endl;
    auto start_cpu = std::chrono::high_resolution_clock::now();
    matrixMulCPU(h_A, h_B, h_C_cpu);
    auto end_cpu = std::chrono::high_resolution_clock::now();
    
    // Compare results
    std::cout << "Comparing results..." << std::endl;
    bool resultsMatch = compareMatrices(h_C_cpu, h_C_gpu, 1e-4f, 1e-4f);
    
    // Output performance information
    auto gpu_duration = std::chrono::duration_cast<std::chrono::microseconds>
                        (end_gpu - start_gpu).count();
    auto cpu_duration = std::chrono::duration_cast<std::chrono::microseconds>
                        (end_cpu - start_cpu).count();
    
    std::cout << "\n=== Performance Results ===" << std::endl;
    std::cout << "GPU execution time: " << gpu_duration << " microseconds (" 
              << gpu_duration / 1000.0 << " ms)" << std::endl;
    std::cout << "CPU execution time: " << cpu_duration << " microseconds (" 
              << cpu_duration / 1000.0 << " ms)" << std::endl;
    if (gpu_duration > 0) {
        std::cout << "Speedup: " << (float)cpu_duration / gpu_duration << "x" << std::endl;
    }
    
    // Print partial results for verification (only for small matrices)
    if (M <= 8 && K <= 8) {
        std::cout << "\n=== First 4x4 elements of matrix C ===" << std::endl;
        std::cout << "CPU results:" << std::endl;
        for (int i = 0; i < std::min(4, M); ++i) {
            for (int j = 0; j < std::min(4, K); ++j) {
                std::cout << std::setw(10) << h_C_cpu.elements[i * K + j] << " ";
            }
            std::cout << std::endl;
        }
        
        std::cout << "\nGPU results:" << std::endl;
        for (int i = 0; i < std::min(4, M); ++i) {
            for (int j = 0; j < std::min(4, K); ++j) {
                std::cout << std::setw(10) << h_C_gpu.elements[i * K + j] << " ";
            }
            std::cout << std::endl;
        }
    }
    
    // Free memory
    delete[] h_A.elements;
    delete[] h_B.elements;
    delete[] h_C_cpu.elements;
    delete[] h_C_gpu.elements;
    
    CHECK(cudaFree(d_A.elements));
    CHECK(cudaFree(d_B.elements));
    CHECK(cudaFree(d_C.elements));
    
    if (resultsMatch) {
        std::cout << "\nValidation passed! GPU and CPU results match." << std::endl;
    } else {
        std::cout << "\nValidation failed! GPU and CPU results do not match." << std::endl;
    }
}

int main() {
    std::cout << "CUDA Matrix Multiplication (Shared Memory Optimization) Validation" << std::endl;
    std::cout << "==================================================================" << std::endl;
    
    // Test cases with different matrix sizes
    // For simplicity, we'll use a simpler approach without tuples
    int testCases[][3] = {
        {16, 17, 20},    // Small size, exactly tile size
        {32, 32, 32},    // Small size, 2x tile size
        {64, 64, 64},    // Medium size
        {128, 128, 128}, // Medium-large
        {256, 256, 256}, // Large size
        {522, 768, 1024}  // Very large size
    };
    
    int numTestCases = sizeof(testCases) / sizeof(testCases[0]);
    
    for (int i = 0; i < numTestCases; i++) {
        int M = testCases[i][0];
        int N = testCases[i][1];
        int K = testCases[i][2];
        
        validateMatrixMul(M, N, K);
        std::cout << "\n" << std::string(50, '=') << "\n" << std::endl;
    }
    
    return 0;
}

算法细节讲解

1、结果矩阵划分

首先我们按照BLOCK_SIZE * BLOCK_SIZE 的大小为一组子矩阵，将C矩阵 划成多个子矩阵C_sub，然后我们在计算C_sub内的一个元素时，使用一个单独的线程thread 。一个C_sub有BLOCK_SIZE * BLOCK_SIZE个待求解的元素，所以在计算一个C_sub时，会有BLOCK_SIZE * BLOCK_SIZE个thread同时工作。

故在代码中，可以看到一个内核函数，一开始就使用bx、by、tx、ty确定了这个内核函数是在哪个block的哪个thread上面运行的。

cpp 复制代码 
__global__ void matrixMulSharedKernel(const Matrix A, const Matrix B, Matrix C) {
    // Shared memory declaration
    __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];
    
    // Thread indices
    int bx = blockIdx.x;
    int by = blockIdx.y;
    int tx = threadIdx.x;
    int ty = threadIdx.y;

2、share

我们声明了两块共享内存，但是你需要知道之所以称之为共享，是因为这一个内核函数在执行时，并不会把这两块内存都写满，而是只写其中一部分。另外，如果以上图为例的话，我们会分为2轮来计算C_sub中的一个元素，因为矩阵A的宽度刚好够塞两个BLOCK。所以在代码中我们会看到一个for循环来控制轮数。

每个线程在每一轮都会将两个元素（一个来自A，一个来自B）放到共享内存中去，还记得之前我有说BLOCK_SIZE * BLOCK_SIZE个thread同时工作吗？所以在很短的时间内，大家一齐将A的左边的block 和B的上面的block都加载进了共享内存As和Bs，由于共享内存是一块很小但是性能异常卓越的处理单元，所以在这上面，计算速度要快于普通的全局内存。

对应的代码如下，这里的if-else对于边界进行了控制；在for循环的每一轮内，只存取两个元素。注意到[ty][tx]，很明显的说明了，一个线程对应的内核函数只会掌管其在As、Bs上对应的一块区域。

cpp 复制代码 
    // (A.width + BLOCK_SIZE - 1) / BLOCK_SIZE是A.width/BLOCK_SIZE向上取整的标准写法，具有普适性    
    for (int m = 0; m < (A.width + BLOCK_SIZE - 1) / BLOCK_SIZE; ++m) { 

        if (row < A.height && (m * BLOCK_SIZE + tx) < A.width) {
            As[ty][tx] = getElement(A, row, m * BLOCK_SIZE + tx);
        } else {
            As[ty][tx] = 0.0f;
        }
        
        if ((m * BLOCK_SIZE + ty) < B.height && col < B.width) {
            Bs[ty][tx] = getElement(B, m * BLOCK_SIZE + ty, col);
        } else {
            Bs[ty][tx] = 0.0f;
        }

如果超出边界，则赋值为0，不会影响计算。这对于A B矩阵含有padding的情况是有用的。

3、__syncthreads()

它保证了在所有线程都加载完毕之后，代码才进行到下面的计算流程。就像小学放学时间，班主任需要等一个班的孩子们都到齐、全站好队了，才带队出校门把孩子送到家长手里。

4、多轮计算

以下图为例，C_sub中的某一个元素，并不是一次性计算出来的，需要在for循环外先声明一个Cvalue，然后在for循环的每一轮中累加。在下图中，不同的颜色表示了for循环不同的轮次。所以在第一个轮次结束后，C_sub中的每个元素都只计算了一半的结果出来 ，**同样的，需要有__syncthreads()加锁，等到同block的所有线程执行第一轮计算完毕才会进入下一轮，**待到第二轮完毕，C_sub的元素就整个算出来了。

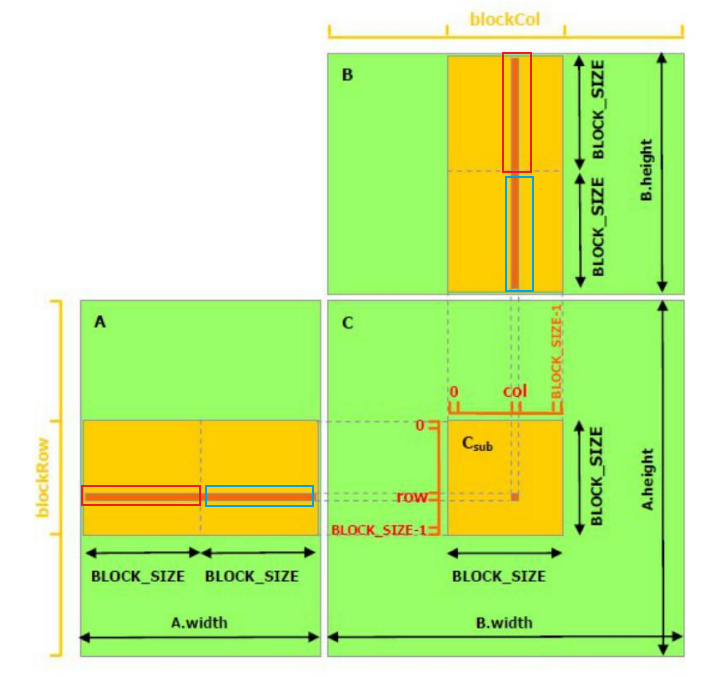
cpp 复制代码 
    float Cvalue = 0.0f;
    
    for (int m = 0; m < (A.width + BLOCK_SIZE - 1) / BLOCK_SIZE; ++m) { // (A.width + BLOCK_SIZE - 1) / BLOCK_SIZE是A.width/BLOCK_SIZE向上取整的标准写法，适用所有未知情况。

        if (row < A.height && (m * BLOCK_SIZE + tx) < A.width) {
            As[ty][tx] = getElement(A, row, m * BLOCK_SIZE + tx);
        } else {
            As[ty][tx] = 0.0f;
        }
        
        if ((m * BLOCK_SIZE + ty) < B.height && col < B.width) {
            Bs[ty][tx] = getElement(B, m * BLOCK_SIZE + ty, col);
        } else {
            Bs[ty][tx] = 0.0f;
        }
        
        __syncthreads();
        
        for (int k = 0; k < BLOCK_SIZE; ++k) {
            Cvalue += As[ty][k] * Bs[k][tx];
        }
        
        __syncthreads();
    }

5、赋值

for循环结束后，Cvalue的值写入到C矩阵中

cpp 复制代码 
    if (row < C.height && col < C.width) {
        setElement(C, row, col, Cvalue);
    }

需要注意row和col的计算

cpp 复制代码 
    int row = by * BLOCK_SIZE + ty;
    int col = bx * BLOCK_SIZE + tx;

它们其实是和划分方式相关的，

cpp 复制代码 
    dim3 blockSize(BLOCK_SIZE, BLOCK_SIZE);
    dim3 gridSize((K + BLOCK_SIZE - 1) / BLOCK_SIZE, 
                  (M + BLOCK_SIZE - 1) / BLOCK_SIZE);
  
    
    matrixMulSharedKernel<<<gridSize, blockSize>>>(d_A, d_B, d_C);

这里的by，bx是grid中的block的坐标，在上图中，C矩阵中橙色的C_sub的坐标是(1,1)，所以我们根据by，bx先找到选中的块，再通过ty、tx找到具体的某个线程，那么C_sub的某个元素的位置也随之确定。

6、stride

这里先理解一下stride是什么

假设有一个3x3的矩阵

复制代码 
[ 1, 2, 3 ]
[ 4, 5, 6 ]
[ 7, 8, 9 ]

在内存中，是行存储的，

复制代码 
[1, 2, 3, 4, 5, 6, 7, 8, 9]

  • width = 3（每行3个元素）

  • height = 3（共3行）

  • stride = width = 3（从一行开始到下一行开始需要跨越3个元素）

cpp 复制代码 
index = row * stride + col = 1 * 3 + 2 = 5
elements[5] = 6

有时出于内存对齐或性能考虑，我们在每行末尾添加padding：

复制代码 
[1, 2, 3, X, 4, 5, 6, X, 7, 8, 9, X]

假设我们添加了1个元素的padding：

  • width = 3（每行实际数据3个元素）

  • height = 3（共3行）

  • stride = 4（包含padding后，每行占用4个元素）

cpp 复制代码 
index = row * stride + col = 1 * 4 + 2 = 6
elements[6] = 6

在CUDA矩阵乘法内核中，stride 的主要作用有：

  1. 处理子矩阵 ：如果mat是一个更大矩阵的子矩阵，stride等于原始矩阵的宽度，而不是子矩阵的宽度。

  2. 内存对齐 ：CUDA性能优化通常要求内存地址对齐，使用stride可以确保每行从对齐的地址开始。

  3. 灵活的矩阵布局：允许矩阵以不同的步长存储在内存中。

我们这里的stride，其实是定义了对齐方式，这样不论矩阵有没有padding，都可以顺利应对。

原理解析

为什么全局内存方案比共享内存慢？

1、CUDA 存储器层次的延迟 / 带宽差异，以及矩阵乘法的 "访存局部性" 被全局内存浪费。

CUDA 存储器的延迟和带宽呈数量级差距，以下是典型架构（如 Volta/Turing）的对比：

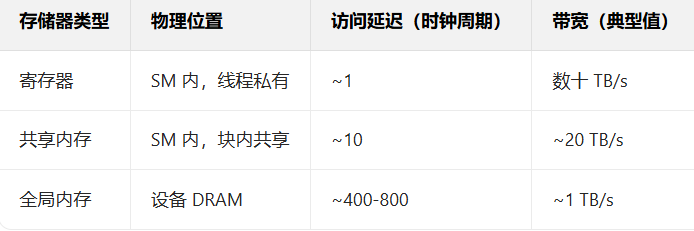
可见：共享内存的延迟是全局内存的 1/40 ~ 1/80，带宽是其 20 倍以上。

2、矩阵乘法的 "重复访存" 问题

矩阵乘法 C = A × B 的核心是 "点积"：C[i][j] = Σ(A[i][k] × B[k][j])（k 遍历维度）。假设用 线程 (i,j) 计算 C [i][j]，且未用共享内存：

  • 对于 A 矩阵：同一行 A[i][0...N-1] 会被计算 C[i][0...N-1] 的所有线程重复读取（每行被读 N 次）；
  • 对于 B 矩阵：同一列 B[0...N-1][j] 会被计算 C[0...N-1][j] 的所有线程重复读取（每列被读 N 次）；

全局内存方案 ：每个线程独立从全局内存读取 A/B 的元素，导致同一数据被全局内存重复加载 N 次 ------ 全局内存的低带宽被彻底耗尽，大量时间浪费在 "等数据" 上。

共享内存方案 ：将 A、B 矩阵划分为 "子块（Tile）"，线程块先一次性从全局内存读取 A 的子块、B 的子块到共享内存（仅读 1 次），然后块内所有线程共享这些数据完成点积计算。→ 全局内存的访问次数从 O(N³) 降至 O(N³ / TileSize)，彻底减少重复访存。

3、全局内存的 "非合并访问" 加剧性能损耗

全局内存的带宽只有在合并访问（Coalesced Access） 时才能达到峰值：即同一 warp（32 线程）的连续线程访问全局内存的连续地址。

但矩阵乘法中：

  • 读取 A 矩阵的行：天然是连续地址，可合并；
  • 读取 B 矩阵的列：线程按列访问时，地址是离散的（步长 = 矩阵宽度），导致非合并访问 ------ 全局内存的有效带宽直接折损（甚至只剩 1/10）。

而共享内存可通过 "转置子块" 等方式，将 B 矩阵的列访问转为共享内存的行访问，既利用共享内存的高带宽，又保证全局内存的合并读取。

相关推荐
Hcoco_me2 小时前
大模型面试题19：梯度消失&梯度爆炸 纯白话文版
人工智能·rnn·深度学习·自然语言处理·word2vec
fufu03112 小时前
Linux环境下的C语言编程（四十八）
数据结构·算法·排序算法
Yingye Zhu(HPXXZYY)2 小时前
Solution to Luogu P6340
算法
小熳芋3 小时前
单词搜索- python-dfs&剪枝
算法·深度优先·剪枝
Xの哲學3 小时前
Linux SLAB分配器深度解剖
linux·服务器·网络·算法·边缘计算
bu_shuo3 小时前
MATLAB中的转置操作及其必要性
开发语言·算法·matlab
是店小二呀3 小时前
在 AtomGit 昇腾 Atlas 800T上解锁 SGLang：零成本打造高性能推理服务
人工智能·pytorch·深度学习·npu
万事可爱^3 小时前
GitCode+昇腾部署Rnj-1模型实践教程
人工智能·深度学习·语言模型·gitcode·本地部署·昇腾npu
高洁013 小时前
图神经网络初探（2）
人工智能·深度学习·算法·机器学习·transformer
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击03电脑检测软件—图吧工具箱043D 圣诞树网页代码05Linux下V2Ray安装配置指南06UV安装并设置国内源07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08jdk21下载、安装（Windows、Linux、macOS）09Claude Code Skills 实用使用手册10Gemini3 生成的基于手势控制3D粒子圣诞树