目录
[1.1 混淆矩阵](#1.1 混淆矩阵)
[1.2.1 准确率(Accuracy)](#1.2.1 准确率(Accuracy))
[编辑1.2.2 精确率(Precision)](#编辑1.2.2 精确率(Precision))
[1.2.3 召回率(Recall,TPR)](#1.2.3 召回率(Recall,TPR))
[1.2.4 假阳性率(FPR)](#1.2.4 假阳性率(FPR))
[1.2.5 F1-Score](#1.2.5 F1-Score)
[1.3 ROC曲线,PR曲线,AUC,AP](#1.3 ROC曲线,PR曲线,AUC,AP)
[1.3.1 ROC 曲线:看模型 "区分正负例" 的能力](#1.3.1 ROC 曲线:看模型 “区分正负例” 的能力)
[1.3.2 PR 曲线:看模型 "在阳性样本中" 的精准度](#1.3.2 PR 曲线:看模型 “在阳性样本中” 的精准度)
[1.3.3 AUC:给曲线一个 "量化分数"](#1.3.3 AUC:给曲线一个 “量化分数”)
[1.3.4 AP](#1.3.4 AP)
[2. 多分类任务](#2. 多分类任务)
[2.1 混淆矩阵](#2.1 混淆矩阵)
[2.2 宏平均(Macro-Average)](#2.2 宏平均(Macro-Average))
[2.3 微平均(Micro-Average)](#2.3 微平均(Micro-Average))
[3.1 基础误差指标](#3.1 基础误差指标)
[3.2 相对误差指标](#3.2 相对误差指标)
[3.3 拟合优度指标](#3.3 拟合优度指标)
1.二分类任务
1.1 混淆矩阵
混淆矩阵是机器学习中用于评估分类模型性能的重要工具,它展示了模型预测结果与真实标签之间的对应关系。通过混淆矩阵,我们可以计算出多种评估指标,如精确率、准确率、F1-Score等。下面我将详细解释这些概念,并说明如何理解和应用它们。
混淆矩阵是一个N×N的表格(N为类别数),用于展示分类模型预测结果与真实标签的对比情况。对于二分类问题,它是最常见的2×2矩阵:
|--------------|--------------|--------------|
| | 预测为正例(P) | 预测为负例(N) |
| 实际为正例(P) | 真正例 (TP) | 假负例 (FN) |
| 实际为负例(N) | 假正例 (FP) | 真负例 (TN) |
- TP:模型正确预测为正例的数量(猜对了正例)
- FP:模型错误预测为正例的数量(把负例猜成了正例)
- FN:模型错误预测为负例的数量(把正例猜成了负例)
- TN:模型正确预测为负例的数量(猜对了负例)
现在假设我们有一个医疗诊断模型:
-
正例:患病
-
负例:健康
|-----------|-----------|-----------|
| | 预测:患病 | 预测:健康 |
| 实际:患病 | TP = 80 | FN = 20 |
| 实际:健康 | FP = 15 | TN = 185 |
解读:
- TP=80:80个病人被正确诊断为患病
- FN=20:20个病人被误诊为健康(漏诊,很危险!)
- FP=15:15个健康人被误诊为患病(误诊,造成不必要的恐慌)
- TN=185:185个健康人被正确诊断为健康
1.2评估指标
|--------------|--------------|--------------|
| | 预测为正例(P) | 预测为负例(N) |
| 实际为正例(P) | 真正例 (TP) | 假负例 (FN) |
| 实际为负例(N) | 假正例 (FP) | 真负例 (TN) |
1.2.1 准确率(Accuracy)
准确率表示模型正确分类的样本占总样本数的比例
1.2.2 精确率(Precision)
精确率表示模型预测为正类别的样本中有多少是真正的正类别
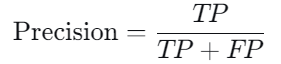
1.2.3 召回率(Recall,TPR)
是指在所有实际为正类别的样本中,模型能够正确预测为正类别的比例
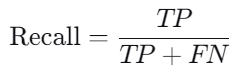
1.2.4 假阳性率(FPR)
负样本中,被误判为正的比例
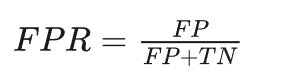
1.2.5 F1-Score
F1 分数是精确率和召回率的调和平均数,它综合了两者的性能
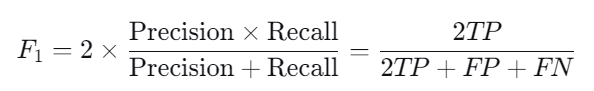
为什么需要F1-Score?
精确率和召回率通常相互矛盾:提高一个往往会降低另一个
F1-Score在两者之间寻找平衡点
不同场景下的指标选择
| 应用场景 | 重要指标 | 原因 |
|---|---|---|
| 垃圾邮件检测 | 精确率 | 不能把正常邮件误判为垃圾邮件 |
| 疾病诊断 | 召回率 | 不能漏诊病人 |
| 搜索引擎 | 精确率 + 召回率 | 既要相关结果,又要全面 |
| 欺诈检测 | 召回率 + 精确率 | 要找出所有欺诈,同时减少误报 |
| 平衡数据集 | 准确率 | 各类别数量相近时有效 |
1.3 ROC曲线,PR曲线,AUC,AP
1.3.1 ROC 曲线:看模型 "区分正负例" 的能力
ROC 曲线的横轴是假阳性率(FPR) ,纵轴是召回率(Recall)。它的本质是:通过调整模型的 "判断阈值"(比如模型认为概率≥0.5 算阳性,调整这个 0.5),画出不同阈值下 FPR 和 Recall 的对应关系。
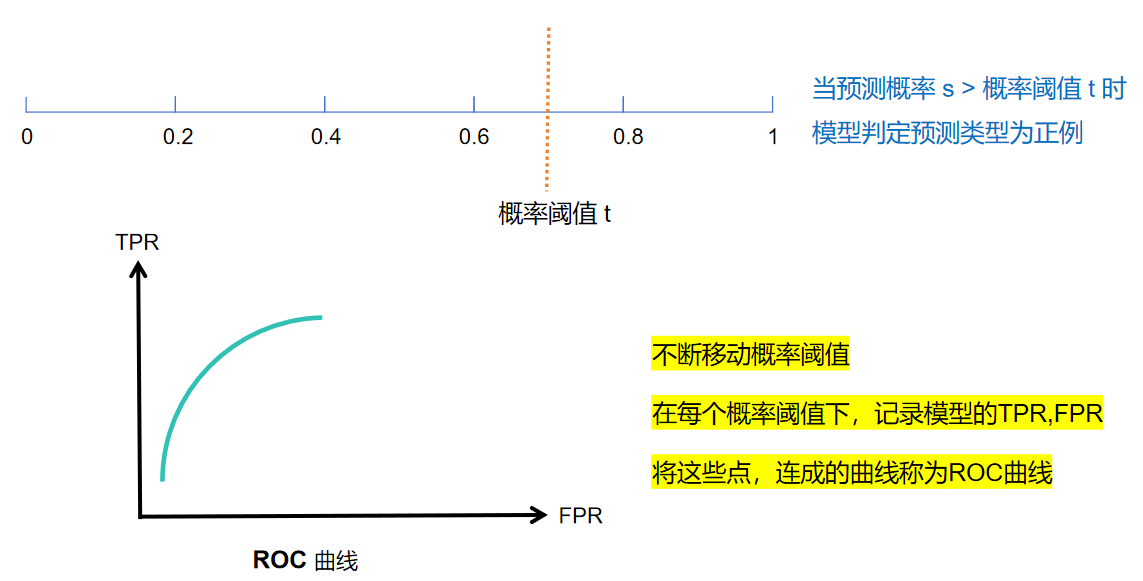
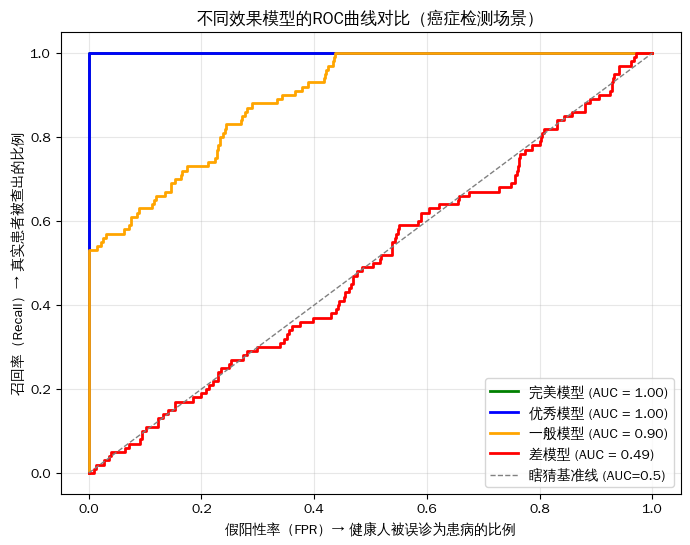
不同效果模型的ROC曲线图:
所以这里,我们就有了一种模型概率阈值的选择方法:
而在一些业务错误代价严重不对称的场景(如医疗,金融),常使用代价敏感法来寻找阈值:
而在统计学中,两类错误代价相等的情况下,我们也会使用Youden指数(J统计量)来 寻找分类的概率阈值:
1.3.2 PR 曲线:看模型 "在阳性样本中" 的精准度
PR 曲线的横轴是召回率(Recall) ,纵轴是精确率(Precision) 。它专注于 "阳性样本" 的表现,特别适合样本极度不均衡的场景(比如罕见病:1 万个样本里只有 10 个患者)
当负样本远多于正样本时:
ROC曲线可能"欺骗"你:FPR = FP/(FP+TN) 中,巨大的TN会稀释FP的影响,导致FPR看起来很低
PR曲线更诚实:Precision = TP/(TP+FP) 直接暴露FP的代价,不受TN数量影响
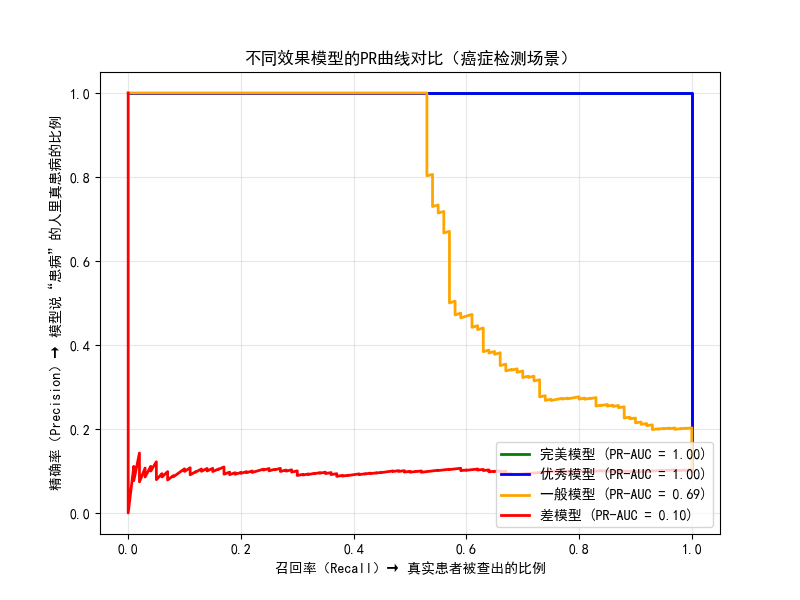
真实反映正类预测质量:直接评估"当模型说它是正类时,有多可信"
业务对齐性强:精确率=成本,召回率=覆盖率,易于业务方理解
极端阈值敏感:在极高置信度区域仍能有效区分模型
1.3.3 AUC:给曲线一个 "量化分数"
AUC 是 "ROC 曲线下的面积",取值范围 0-1,是衡量模型性能的 "黄金指标"
怎么解读 AUC 值?
- AUC=1:完美模型(零误诊、全查全),现实中几乎不存在。
- 0.8<AUC<1:优秀模型(区分能力强)。
- 0.5<AUC<0.8:一般模型(有一定区分能力,但需要优化)。
- AUC=0.5:垃圾模型(和瞎猜一样)。
- AUC<0.5:反向模型(还不如瞎猜,把预测结果反过来就能变好)
1.3.4 AP
- 定义:以 Recall 为横轴、Precision 为纵轴绘制 P-R 曲线,曲线下的面积即为 AP。
- 意义:避免单一阈值下 Precision/Recall 的局限性,全面反映单类目标在不同召回率下的精确率表现。
- 作用:比 F1-Score 更细腻地量化单类目标的检测能力,是单类别算法对比的核心指标。
2. 多分类任务
2.1 混淆矩阵
假设我们有一个疾病诊断模型,需要在1000名患者中识别三种疾病:
- A类:感冒(常见)
- B类:肺炎(中等)
- C类:过敏(罕见)
模型预测结果如下(混淆矩阵):
| 真实\预测 | A类(感冒) | B类(肺炎) | C类(过敏) | 总计 |
|---|---|---|---|---|
| A类 | 450 (TP_A) | 30 | 20 | 500 |
| B类 | 40 | 280 (TP_B) | 30 | 350 |
| C类 | 10 | 10 | 130 (TP_C) | 150 |
| 总计 | 500 | 320 | 180 | 1000 |
我们可以先计算出A,B,C三个类对应的精确率(Precision)和召回率(Recall):
A类(感冒):
- 精确率(Precision)= 450 / 500 = 0.9
- 召回率(Recall)= 450 / 500 =0.9
B类(肺炎):
- 精确率(Precision)= 280 / 320 = 0.875
- 召回率(Recall)= 280 / 350 = 0.80
C类(过敏):
- 精确率(Precision)= 130 /180 = 0.722
- 召回率(Recall)= 130 / 150 = 0.867
2.2 宏平均(Macro-Average)
计算方式: 先对每个类别的指标单独计算,再求算术平均。
-
宏精确率 = (0.90 + 0.875 + 0.722) / 3 = 0.832
-
宏召回率 = (0.90 + 0.80 + 0.867) / 3 = 0.856
-
宏F1 = 2 × 宏精确率 × 宏召回率 / (宏精确率 + 宏召回率) = 0.844
宏平均的作用
-
平等对待每个类别:不管类别样本多少,都赋予相同权重
-
反映模型在所有类别上的均衡表现:能发现模型在稀有类别(C类过敏)上的不足
-
适合场景 :当每个类别都同等重要时,如疾病诊断中,不能因为过敏罕见就忽视它
关键特点 :宏平均对稀有类别更敏感 。如果C类表现很差(比如精确率只有0.2),宏平均值会明显降低,起到警示作用。
2.3 微平均(Micro-Average)
计算方式: 先汇总所有类别的TP、FP、FN,再统一计算指标。
-
总TP = 450 + 280 + 130 = 860
-
总FP = (30+20) + (40+30) + (10+10) = 140 (所有非对角线预测值)
-
总FN = (30+20) + (40+30) + (10+10) = 140 (所有非对角线真实值)
-
微精确率 = 总TP / (总TP + 总FP) = 860 / (860 + 140) = 0.86
-
微召回率 = 总TP / (总TP + 总FN) = 860 / (860 + 140) = 0.86
-
微F1 = 2 × 0.86 × 0.86 / (0.86 + 0.86) = 0.86
微平均的作用
-
样本加权:大样本类别(感冒占50%)贡献更大,小样本类别影响较小
-
反映总体预测准确性 :更关注模型在所有样本上的整体表现
-
适合场景 :当关注整体效率 而非单个类别时,如大规模用户行为分析(点击/购买/忽略)
关键特点 :微平均对大类别更敏感。即使C类(过敏)预测得不好,只要A类(感冒)预测得好,微平均值仍可能较高。
宏平均像"各科老师的平均分",不能偏科;微平均像"全校总分",重点科目权重更大。
维度 宏平均(Macro) 微平均(Micro) 计算逻辑 先算每个类别的指标,再平均 先汇总所有类别的统计量,再算指标 类别权重 每个类别权重相同(平等对待) 样本多的类别权重更高(按样本量加权) 对不平衡数据的敏感度 对少数类敏感(反映其性能) 对多数类敏感(受其主导) 适用场景 需关注每个类别的表现(如罕见病识别) 需关注整体样本的表现(如大规模分类)
3.回归任务
3.1 基础误差指标



3.2 相对误差指标

3.3 拟合优度指标