深度学习基础知识总结（一）：深入理解卷积（Convolution)

在深度学习的世界中，卷积（Convolution）无疑是最核心的概念之一。无论是图像识别、目标检测，还是语音处理、自然语言理解，卷积操作都扮演着"特征提取"的重要角色。今天我们就从最基础的角度，带你彻底搞懂卷积的原理与作用。

一、为什么需要卷积？

在卷积神经网络（CNN）出现之前，我们处理图像的方式往往依赖"全连接层"。但图像的像素数量巨大，例如一张 224×224 的彩色图片有超过 15 万个输入特征，这样的网络不仅参数多，而且难以捕捉局部信息。

卷积操作的出现，正是为了解决这两个问题：

参数共享（Parameter Sharing） ------ 一个卷积核在整个图像上滑动，同一个权重组反复使用，大幅减少参数数量。
局部感受野（Local Receptive Field） ------ 卷积操作只关注局部区域，能够有效捕捉局部特征，如边缘、角点等。

二、卷积的数学原理

以二维卷积为例，假设输入为一张灰度图像 III，卷积核（Filter）为 KKK，卷积操作可表示为：

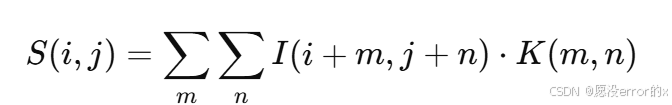
通俗地说，就是把卷积核在图像上滑动，每次计算核内像素与图像对应区域像素的加权和。

复制代码

输入图像 (5×5)             卷积核 (3×3)
------------------         --------------
|1 2 3 0 1|                |1 0 1|
|0 1 2 3 1|                |0 1 0|
|1 0 1 2 3|                |1 0 1|
|2 1 0 1 2|
|3 2 1 0 1|

当卷积核位于图像左上角时，计算：

复制代码

(1×1 + 2×0 + 3×1 + 0×0 + 1×1 + 2×0 + 1×1 + 0×0 + 1×1) = 9

如此滑动卷积核，就得到了新的特征图（Feature Map）。

三、步长（Stride）与填充（Padding）

卷积并非只有"滑动+乘法"这么简单，步长和填充是影响输出特征图大小的重要因素。

步长（Stride） ：卷积核每次滑动的像素数。步长越大，输出尺寸越小。你可以把卷积核想象成一个"放大镜"，在图像上滑动，观察局部区域。
当 步长 = 1 时，相当于放大镜"挪一步看一格"，观察得很仔细，每个像素几乎都被覆盖；
当 步长 = 2 时，相当于"隔一格看一格"，看得更快，但细节信息丢失一些；
当 步长 = 3 时，就像"走大步子"，只挑关键点看一眼，图像被大幅压缩。
填充（Padding） ：在图像边缘补零，使输出尺寸与输入一致（常见的有 same 和 valid 两种）。假设我们卷积一张 5×5 的猫脸图片，使用 3×3 卷积核。如果不填充，最外面一圈像素（比如猫的胡须）几乎不会被卷积核看到；如果我们 在四周补一圈 0（Padding=1），那么卷积核就可以"看到"整张猫脸的每个区域。

计算公式如下：

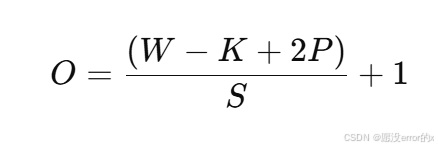
其中：

O：输出尺寸
W：输入尺寸
K：卷积核大小
P：填充大小
S：步长

四、卷积层在CNN中的作用

在深度学习模型中，不同层的卷积有不同的"职责"：

卷积层类型	提取特征层次	举例说明
第一层卷积	低级特征	边缘、线条、颜色变化
中间层卷积	中级特征	纹理、形状、局部结构
深层卷积	高级特征	语义信息（如"猫的脸"、"汽车轮胎"）

卷积层叠加后，网络就能逐渐从像素级信息中学习到抽象语义，这正是深度学习强大的原因所在。

五、卷积的类型

普通卷积（Standard Convolution）

最常见的形式，卷积核在所有通道上作用。
深度可分离卷积（Depthwise Separable Convolution）

被 MobileNet 等轻量化模型采用，先对每个通道独立卷积（Depthwise），再做通道融合（Pointwise）。
空洞卷积（Dilated Convolution）

用于扩大感受野而不增加参数量，常见于语义分割网络（如 DeepLab）。

六、可视化卷积：看见模型在看什么

一个有趣的实践是"卷积可视化"：

通过展示卷积核或特征图，我们可以看到网络学习到的模式。例如，第一层的卷积核通常类似"边缘检测器"，而高层卷积核则捕捉到语义结构。

复制代码

# 示例代码：可视化卷积核
import torch
import torchvision.models as models
import matplotlib.pyplot as plt

model = models.vgg16(pretrained=True)
weights = model.features[0].weight.data  # 第一层卷积权重

plt.figure(figsize=(10, 10))
for i in range(16):
    plt.subplot(4, 4, i + 1)
    plt.imshow(weights[i][0].cpu(), cmap='gray')
    plt.axis('off')
plt.show()

七、总结

卷积的核心思想就是局部连接 + 参数共享，它让神经网络既高效又强大。理解卷积不仅能帮助我们掌握 CNN 的原理，也为后续学习池化（Pooling）、激活函数（ReLU）、批归一化（BatchNorm）等知识打下坚实基础。

在下一篇文章中，我们将继续深入讲解 ------ 激活函数（Activation Function） 的作用与设计思想。