重温 Java 21 之密钥封装机制 API

aneasystone本尊2025-11-14 8:34

密钥封装（Key Encapsulation） 是一种现代加密技术，它使用非对称或公钥加密来保护对称密钥。传统的做法是使用公钥加密随机生成的对称密钥，但这需要 填充（Paddings） 并且难以证明安全，密钥封装机制（Key Encapsulation Mechanism，KEM） 另辟蹊径，使用公钥的属性来推导相关的对称密钥，不需要填充。

KEM 的概念是由 Crammer 和 Shoup 在 Design and Analysis of Practical Public-Key Encryption Schemes Secure against Adaptive Chosen Ciphertext Attack 这篇论文中提出的，后来 Shoup 将其提议为 ISO 标准，并于 2006 年 5 月接受并发布为 ISO 18033-2。

经过多年的发展，KEM 已经在多个密码学领域有所应用：

Java 平台中现有的加密 API 都无法以自然的方式表示 KEM，第三方安全提供商的实施者已经表达了对标准 KEM API 的需求。于是，Java 21 引入了一种新的 KEM API，使应用程序能够自然且方便地使用 KEM 算法。

对称加密

上面对 KEM 的描述中涉及大量现代密码学的概念，为了对 KEM 有一个更直观的认识，我们不妨快速浏览一遍密码学的发展历史。

我们经常会在各种讲述一二战的谍战片中看到破译电报的片段，当时使用的密码算法在现在看来是非常简单的，几乎所有的密码系统使用的都是 对称加密（Symmetric Cryptography） 算法，也就是说使用相同的密钥进行消息的加密与解密，因为这个特性，我们也称这个密钥为 共享密钥（Shared Secret Key）。

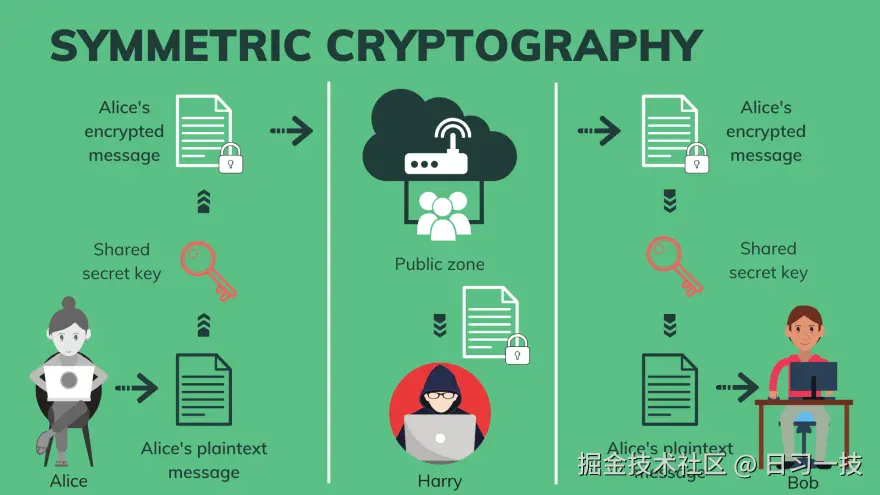
常见的对称加密算法有：DES、3DES、AES、Salsa20 / ChaCha20、Blowfish、RC6、Camelia 等。

其中绝大多数都是 块密码算法（Block Cipher） 或者叫 分组密码算法 ，这种算法一次只能加密固定大小的块（例如 128 位）；少部分是 流密码算法（Stream Cipher） ，流密码算法将数据逐字节地加密为密文流。为了实现加密任意长度的数据，我们通常需要将分组密码算法转换为流密码算法，这被称为 分组密码的工作模式，常用的工作模式有：ECB（电子密码本）、CBC（密码块链接）、CTR（计数器）、CFB（密文反馈模式）、OFB（输出反馈模式）、GCM（伽罗瓦/计数器模式）） 等。

分组密码的工作模式其背后的主要思想是把明文分成多个长度固定的组，再在这些分组上重复应用分组密码算法，以实现安全地加密或解密任意长度的数据。某些分组模式（如 CBC）要求将输入拆分为分组，并使用填充算法（例如添加特殊填充字符）将最末尾的分组填充到块大小，也有些分组模式（如 CTR、CFB、OFB、CCM、EAX 和 GCM）根本不需要填充，因为它们在每个步骤中，都直接在明文部分和内部密码状态之间执行异或（XOR）运算。

因此我们在使用对称加密时，往往要指定 工作模式（Modes） 和 填充模式（Paddings） 这两个参数，下面是使用 Java 标准库提供的接口实现 AES 加密和解密的示例：

java 复制代码 
private static void testAES() throws Exception {

  // 1. 生成对称密钥
  KeyGenerator keyGenerator = KeyGenerator.getInstance("AES");
  keyGenerator.init(new SecureRandom());
  Key secretKey =  keyGenerator.generateKey();

  // 1. 使用固定密钥：128 位密钥 = 16 字节
  // SecretKey secretKey = new SecretKeySpec("1234567890abcdef".getBytes(), "AES");

  // 2. 加密
  Cipher cipher = Cipher.getInstance("AES/ECB/PKCS5Padding");
  cipher.init(Cipher.ENCRYPT_MODE, secretKey);
  byte[] encrypted = cipher.doFinal("hello".getBytes());

  // 3. 解密
  cipher.init(Cipher.DECRYPT_MODE, secretKey);
  byte[] decrypted = cipher.doFinal(encrypted);
  System.out.println(new String(decrypted));
}

我们首先通过 KeyGenerator 生成一个对称密钥（也可以直接使用 SecretKeySpec 来定义一个固定的密钥，但是要注意密钥的长度），然后通过 算法名称/工作模式/填充模式 来获取一个 Cipher 实例，这里使用的是 AES 算法，ECB 分组模式以及 PKCS5Padding 填充模式，关于其他算法和模式可参考 Java Security Standard Algorithm Names。得到 Cipher 实例后，就可以对数据进行加密和解密，可以看到，这里加密和解密使用的是同一个密钥。

对称加密算法的问题有两点：

  • 需要安全的通道进行密钥交换，早期最常见的是面对面交换密钥，一旦密钥泄露，数据将完全暴露；
  • 每个点对点通信都需要使用不同的密钥，密钥的管理会变得很困难，如果你需要跟 100 个朋友安全通信，你就要维护 100 个不同的对称密钥；

综上，对称加密会导致巨大的 密钥交换 跟 密钥保存与管理 的成本。

密钥交换协议

为了解决对称加密存在的两大问题，密码学家们前仆后继，想出了各种各样的算法，其中最关键的一个是 Whitfield Diffie 和 Martin Hellman 在 1976 年公开发表的一种算法，也就是现在广为人知的 Diffie--Hellman 密钥交换（Diffie--Hellman Key Exchange，DHKE） 算法。

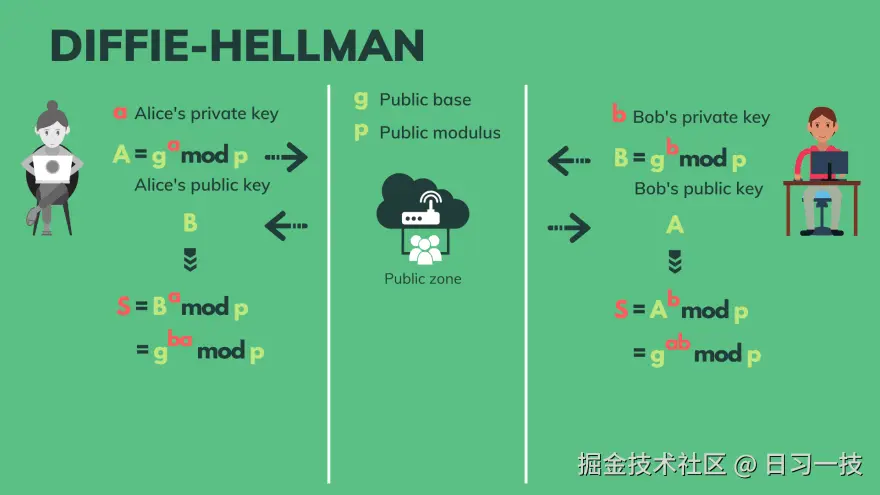
上图是经典 DHKE 协议的整个过程，其基本原理涉及到数学中的 模幂（Modular Exponentiations） 和 离散对数（Discrete Logarithms） 的知识。

模幂是指求 g 的 a 次幂模 p 的值，其中 g a p 均为整数，公式如下：

css 复制代码 
A = (g^a) mod p

而离散对数是指在已知 g p 和模幂值 A 的情况下，求幂指数 a 的逆过程。

我们通过将 p 设置为一个非常大的质数，使用计算机计算上述模幂的值是非常快的，但是求离散对数却非常困难，这也就是所谓的 离散对数难题（Discrete Logarithm Problem，DLP）。

在 DHKE 协议中，Alice 和 Bob 首先约定好两个常数 g 和 p，这两个数所有人都可见。然后他们分别生成各自的私钥 a 和 b，这两个值各自保存，不对外公开。他们再分别使用各自的私钥计算出模幂 A 和 B，这两个值就是他们的公钥：

css 复制代码 
A = (g^a) mod p
B = (g^b) mod p

接着，Alice 将 A 发送给 Bob，Bob 将 B 发送给 Alice，接受到彼此的公钥之后，他们使用自己的私钥来计算模幂：

css 复制代码 
S1 = (B^a) mod p
S2 = (A^b) mod p

根据模幂的数学性质，我们可以得知 S1 和 S2 是相等的！

css 复制代码 
S1 = (B^a) mod p = (g^b)^a mod p = ( g^(b*a) ) mod p
S2 = (A^b) mod p = (g^a)^b mod p = ( g^(a*b) ) mod p

至此 Alice 和 Bob 就协商出了一个共享密钥，这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。可以看到，尽管整个密钥交换过程是公开的，但是任何窃听者都无法根据公开信息推算出密钥，这就是密钥交换协议的巧妙之处。

下面的代码演示了如何在 Java 中实现标准的 DHKE 协议：

java 复制代码 
private static void testKeyAgreement() throws Exception {

  // 1. Alice 和 Bob 分别生成各自的密钥对
  KeyPairGenerator keyPairGen = KeyPairGenerator.getInstance("DH");
  keyPairGen.initialize(512);
  KeyPair keyPairAlice = keyPairGen.generateKeyPair();
  KeyPair keyPairBob = keyPairGen.generateKeyPair();

  // 2. Alice 根据 Bob 的公钥协商出对称密钥
  KeyAgreement keyAgreement = KeyAgreement.getInstance("DH");
  keyAgreement.init(keyPairAlice.getPrivate());
  keyAgreement.doPhase(keyPairBob.getPublic(), true);
  byte[] secretKey1 = keyAgreement.generateSecret();

  // 3. Bob 根据 Alice 的公钥协商出对称密钥
  keyAgreement.init(keyPairBob.getPrivate());
  keyAgreement.doPhase(keyPairAlice.getPublic(), true);
  byte[] secretKey2 = keyAgreement.generateSecret();

  // 4. 比较双方的密钥是否一致
  System.out.println("Alice Secret key: " + HexFormat.of().formatHex(secretKey1));
  System.out.println("Bob Secret key: " + HexFormat.of().formatHex(secretKey2));
}

这里首先通过 KeyPairGenerator 为 Alice 和 Bob 分别生成密钥对（密钥对中包含了一个私钥和一个公钥，也就是上文中的 a/b 和 A/B），然后使用 KeyAgreement.getInstance("DH") 获取一个 KeyAgreement 实例，用于密钥协商，Alice 根据 Bob 的公钥协商出对称密钥 S1，Bob 根据 Alice 的公钥协商出对称密钥 S2，根据输出结果可以看到 S1 和 S2 是相等的。

非对称加密

从第一次世界大战、第二次世界大战到 1976 年这段时期密码的发展阶段，被称为 近代密码阶段 。1976 年是密码学的一个分水岭，在 Whitfield Diffie 和 Martin Hellman 这篇论文 中，他们不仅提出了 DHKE 算法，还提出了 公钥密码学（Public- Key Cryptography） 的概念。

公钥密码学中最核心的部分是 非对称加密（Asymmetric Encryption） 算法，和 DHKE 算法类似，它也是基于两个不同的密钥来实现加密和解密，一个称为公钥，另一个称为私钥，其中公钥可以公开，任何人都能访问；但和 DHKE 不同的是，DHKE 中的公钥只是用于协商出一个对称密钥，用于后续通讯的加解密，而在非对称加密中，不需要密钥协商，消息的发送者可以直接使用接受者的公钥对数据进行加密，而加密后的数据只有私钥的持有者才能将其解密。

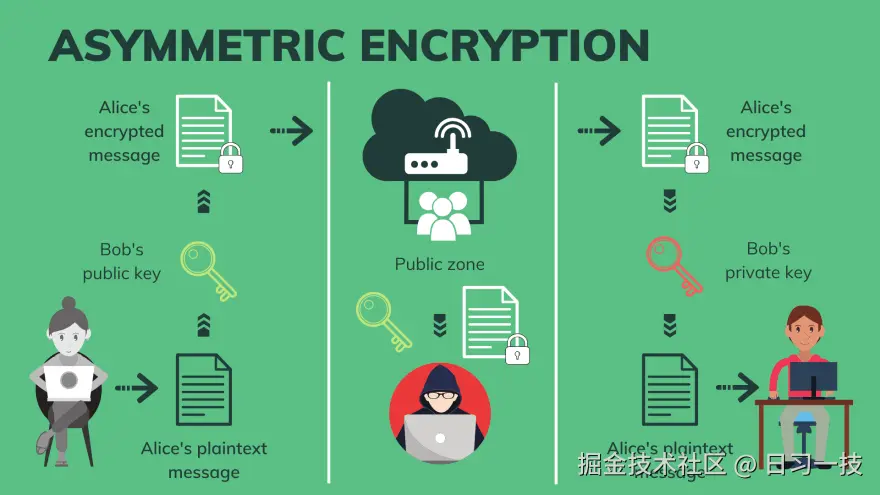
非对称加密算法的这种神奇特性，使得通讯双发不需要预先协商密钥，因此非常适合在多方通信中使用；也使得公钥密码学的概念很快就深入人心，它极大地推动了现代密码学的发展，为 数字签名 和 数字证书 提供了理论基础，特别是 公钥基础设施（PKI） 体系的建立，实现安全的身份验证和数据保护。

可以说，非对称加密是密码学领域一项划时代的发明，它宣告了近代密码阶段的终结，是现代密码学的起点。

最著名的非对称加密算法非 RSA 莫属，它是 1977 年由三位美国数学家 Ron Rivest、Adi Shamir 和 Leonard Adleman 共同设计的，这种算法以他们名字的首字母命名。RSA 算法涉及不少数论中的基础概念和定理，比如 互质 、欧拉函数 、模反元素 、中国余数定理 、费马小定理 等，网上有大量的文章介绍 RSA 算法原理，感兴趣的同学可以查阅相关的资料。

不过对于初学者来说，这些原理可能显得晦涩难懂，不妨玩一玩下面这个数学小魔术：

首先，让 A 任意想一个 3 位数，并把这个数乘以 91，然后将积的末三位告诉 B，B 就可以猜出 A 想的是什么数字。比如 A 想的是 123，那么他就计算出 123 * 91 = 11193，并把结果的末三位 193 告诉 B。那么 B 要怎么猜出对方的数字呢？其实很简单，只需要把对方说的数字再乘以 11，乘积的末三位就是 A 刚开始想的数了。可以验证一下，193 * 11 = 2123，末三位正是对方所想的秘密数字！

这个小魔术的道理其实很简单，由于 91 * 11 = 1001，而任何一个三位数乘以 1001 后，末三位显然都不变，例如 123 * 1001 = 123123。

这个例子直观地展示了非对称加密算法的工作流程：A 和 B 可以看做消息的发送方和接受方，其中 91 是 B 的公钥，123 是 A 要发送的消息，123 * 91 就好比使用公钥加密，193 就是加密后的密文；而 11 是 B 的私钥，193 * 11 就是使用私钥解密。

RSA 算法的本质就是上面这套思想，只不过它不是简单的乘法计算，而是换成了更加复杂的指数和取模运算。

下面继续使用 Java 代码来实现 RSA 的加密和解密：

java 复制代码 
private static void testRSA() throws Exception {

  // 1. Bob 生成密钥对
  KeyPairGenerator keyPairGen = KeyPairGenerator.getInstance("RSA");
  keyPairGen.initialize(2048);
  KeyPair keyPairBob = keyPairGen.generateKeyPair();

  // 2. Alice 使用 Bob 的公钥加密数据
  Cipher cipher1 = Cipher.getInstance("RSA");
  cipher1.init(Cipher.ENCRYPT_MODE, keyPairBob.getPublic());
  byte[] encrypted = cipher1.doFinal("hello".getBytes());

  // 3. Bob 使用自己的私钥解密数据
  Cipher cipher2 = Cipher.getInstance("RSA");
  cipher2.init(Cipher.DECRYPT_MODE, keyPairBob.getPrivate());
  byte[] decrypted = cipher2.doFinal(encrypted);

  System.out.println(new String(decrypted));
}

这里的代码和对称加密如出一辙，都是先通过 Cipher.getInstance() 获取一个 Cipher 实例，然后再通过它对数据进行加密和解密；和对称加密不同的是，这里加密用的是 Bob 的公钥，而解密用的是 Bob 的私钥。

其实，根据非对称加密的性质，我们不仅可以 公钥加密，私钥解密 ，而且也可以 私钥加密，公钥解密 ，不过用私钥加密的信息所有人都能够用公钥解密，这看起来貌似没啥用，但是密码学家们却发现它大有用处，由于私钥加密的信息只能用公钥解密，也就意味着这个消息只能是私钥持有者发出的，其他人是不能伪造或篡改的，所以我们可以把它用作 数字签名，数字签名在数字证书等应用中。

除了 RSA 算法，还有一些其他重要的非对称加密算法，比如 Rabin 密码、ElGamal 密码 以及基于椭圆曲线的 ECC 密码（Elliptic Curve Cryptography） 等。

后量子密码学

非对称加密算法的安全性，基本上都是由不同的数学难题保障的，比如：

这些数学难题暂时都没有好方法解决，所以这些非对称加密算法暂时仍然被认为是安全的；一旦这些数学难题被破解，那么这些加密算法就不再安全了。

近年来，随着 量子计算机 的不断发展，很多运行于量子计算机的量子算法被提出来，其中最著名的是数学家彼得·秀尔于 1994 年提出的 秀尔算法，可以在多项式时间内解决整数分解问题。

这也就意味着，如果攻击者拥有大型量子计算机，那么他可以使用秀尔算法解决整数分解问题，从而破解 RSA 算法。不仅如此，后来人们还发现，使用秀尔算法也可以破解离散对数和椭圆曲线等问题，这导致目前流行的公钥密码系统都是 量子不安全（quantum-unsafe） 的。如果人类进入量子时代，这些密码算法都将被淘汰。

密码学家们估算认为，破解 2048 位的 RSA 需要 4098 个量子比特与 5.2 万亿个托佛利门，目前还不存在建造如此大型量子计算机的科学技术，因此现有的公钥密码系统至少在未来十年（或更久）依然是安全的。尽管如此，密码学家已经积极展开了后量子时代的密码学研究，也就是 后量子密码学（Post-quantum Cryptography，PQC）。

目前已经有一些量子安全的公钥密码系统问世，但是由于它们需要更长的密钥、更长的签名等原因，并没有被广泛使用。这些量子安全的公钥密码算法包括：NewHope、NTRU、BLISS、Kyber 等，有兴趣的同学可以自行查阅相关文档。

混合密码系统

非对称加密好处多多，既可以用来加密和解密，也可以用来签名和验证，而且还大大降低了密钥管理的成本。不过非对称加密也有不少缺点：

  • 使用密钥对进行加解密，算法要比对称加密更复杂；而且一些非对称密码系统（如 ECC）不直接提供加密能力，需要结合使用更复杂的方案才能实现加解密；
  • 只能加解密很短的消息；
  • 加解密非常缓慢，比如 RSA 加密比 AES 慢 1000 倍；

为了解决这些问题，现代密码学提出了 混合密码系统（Hybrid Cryptosystem） 或 混合公钥加密（Hybrid Public Key Encryption，HPKE） 的概念，将对称加密和非对称加密的优势相结合，好比同时装备电动机和发动机两种动力系统的混合动力汽车。发送者首先生成一个对称密码，使用这个对称密码来加密消息，然后使用接受者的公钥来加密对称密码；接受者首先使用自己的私钥解密出对称密码，然后再用对称密码解密消息。这里的对称密码也被称为 会话密钥（Session Key）。

下面的代码演示了 Alice 是如何利用 Bob 的公钥将一个 AES 对称密钥发送给 Bob 的：

java 复制代码 
private static void testRSA_AES() throws Exception {

  // 1. Bob 生成密钥对
  KeyPairGenerator keyPairGen = KeyPairGenerator.getInstance("RSA");
  keyPairGen.initialize(2048);
  KeyPair keyPair = keyPairGen.generateKeyPair();

  // 2. Alice 生成一个对称密钥
  KeyGenerator keyGen = KeyGenerator.getInstance("AES");
  keyGen.init(256);
  SecretKey secretKey = keyGen.generateKey();

  // 3. Alice 使用 Bob 的公钥加密对称密钥
  Cipher cipher1 = Cipher.getInstance("RSA");
  cipher1.init(Cipher.ENCRYPT_MODE, keyPair.getPublic());
  byte[] secretKeyEncrypted = cipher1.doFinal(secretKey.getEncoded());

  // 4. Bob 使用自己的私钥解密出对称密钥
  Cipher cipher2 = Cipher.getInstance("RSA");
  cipher2.init(Cipher.DECRYPT_MODE, keyPair.getPrivate());
  byte[] secretKeyDecrypted = cipher2.doFinal(secretKeyEncrypted);

  // 5. 比较双方的密钥是否一致
  System.out.println("Alice Secret key: " + HexFormat.of().formatHex(secretKey.getEncoded()));
  System.out.println("Bob Secret key: " + HexFormat.of().formatHex(secretKeyDecrypted));
}

可以看出，在混合密码系统中，非对称加密算法的作用和上文中的 DHKE 一样，只是用于密钥交换，并不用于加密消息，这和 DHKE 的工作原理几乎是一样的，所以严格来说，DHKE 也算是一种混合密码系统，只是两种密钥交换的实现不一样罢了。如何将会话密钥加密并发送给对方，就是 密钥封装机制（Key Encapsulation Mechanisms，KEM） 要解决的问题。

密钥封装机制

综上所述，密钥封装机制就是一种基于非对称加密的密钥交换技术，其主要目的是在不直接暴露私钥的情况下安全地传输会话密钥。

在 KEM 中，发起方运行一个封装算法产生一个会话密钥以及与之对应的 密钥封装消息（key encapsulation message） ，这个消息在 ISO 18033-2 中被称为 密文（ciphertext），随后发起方将密钥封装消息发送给接收方，接收方收到后，使用自己的私钥进行解封，从而获得相同的会话密钥。一个 KEM 由三部分组成：

  • 密钥对生成函数：由接收方调用，用于生成密钥对，包含公钥和私钥；
  • 密钥封装函数：由发送方调用，根据接收方的公钥产生一个会话密钥和密钥封装消息，然后发送方将密钥封装消息发送给接收方；
  • 密钥解封函数：由接收方调用，根据自己的私钥和接受到的密钥封装消息，计算出会话密钥。

其中第一步可以由现有的 KeyPairGenerator API 完成，但是后两步 Java 中暂时没有合适的 API 来自然的表示，这就是 JEP 452 被提出的初衷。通过 密钥封装机制 API（KEM API） 可以方便的实现密钥封装和解封：

java 复制代码 
private static void testKEM() throws Exception {

  // 1. Bob 生成密钥对
  KeyPairGenerator keyPairGen = KeyPairGenerator.getInstance("X25519");
  KeyPair keyPair = keyPairGen.generateKeyPair();

  // 2. Alice 根据 Bob 的公钥生成一个 Encapsulated 对象，这个对象里包含了：
  //  * 共享密钥 shared secret
  //  * 密钥封装消息 key encapsulation message
  //  * 可选参数 optional parameters
  //  然后 Alice 将密钥封装消息发送给 Bob
  KEM kem1 = KEM.getInstance("DHKEM");
  Encapsulator sender = kem1.newEncapsulator(keyPair.getPublic());
  Encapsulated encapsulated = sender.encapsulate();
  SecretKey k1 = encapsulated.key();

  // 3. Bob 根据自己的私钥和 Alice 发过来的密钥封装消息，计算出共享密钥
  KEM kem2 = KEM.getInstance("DHKEM");
  Decapsulator receiver = kem2.newDecapsulator(keyPair.getPrivate());
  SecretKey k2 = receiver.decapsulate(encapsulated.encapsulation());

  // 4. 比较双方的密钥是否一致
  System.out.println(Base64.getEncoder().encodeToString(k1.getEncoded()));
  System.out.println(Base64.getEncoder().encodeToString(k2.getEncoded()));
}

从代码可以看出密钥封装机制和混合密码系统有点像，但是看起来要更简单一点，省去了使用 KeyGenerator.generateKey() 生成对称密钥的步骤，而是使用密钥封装算法直接给出，至于这个密钥封装算法可以抽象成任意的实现，可以是密钥生成算法，也可以是随机数算法。

从 Java 文档 中可以看到 KEM 算法暂时只支持 DHKEM 这一种。但是 KEM API 提供了 服务提供商接口（Service Provider Interface，SPI），允许安全提供商在 Java 代码或本地代码中实现自己的 KEM 算法，比如 RSA-KEM、ECIES-KEM、PSEC-KEM、PQC-KEM 等。

欢迎关注

如果这篇文章对您有所帮助，欢迎关注我的同名公众号：日习一技，每天学一点新技术。

我会每天花一个小时，记录下我学习的点点滴滴。内容包括但不限于：

  • 某个产品的使用小窍门
  • 开源项目的实践和心得
  • 技术点的简单解读

目标是让大家用5分钟读完就能有所收获，不需要太费劲，但却可以轻松获取一些干货。不管你是技术新手还是老鸟，欢迎给我提建议，如果有想学习的技术，也欢迎交流！

相关推荐
欢聚赢销CRM2 小时前
从“各自为战“到“数据协同“：销采一体化CRM正在重构供应链竞争力
大数据·人工智能·重构·数据分析
IT_陈寒2 小时前
Python 3.12 新特性实战：10个让你代码更优雅的隐藏技巧
前端·人工智能·后端
说私域2 小时前
基于开源AI智能名片链动2+1模式与S2B2C商城小程序的商家活动策略研究
人工智能·小程序
亚马逊云开发者2 小时前
Agentic AI基础设施实践经验系列（八）：Agent应用的隐私和安全
人工智能
大模型真好玩2 小时前
GPT-5.1 核心特性深度解析，它会是模型性能的新标杆吗？
人工智能
综合热讯2 小时前
微软Office下线“重用幻灯片”功能，WPS反向升级：AI让旧功能焕新生
人工智能·microsoft·wps
xinyu_Jina3 小时前
FIRE之旅 财务计算器：金融独立模型中的复利可视化与敏感性分析
人工智能·程序人生·信息可视化·金融·程序员创富
工藤学编程3 小时前
零基础学AI大模型之Milvus核心：分区-分片-段结构全解+最佳实践
人工智能·milvus
caijingshiye4 小时前
九科信息企业自动化智能体：打破知行割裂，让AI真正动手干活
运维·人工智能·自动化
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件05Linux下V2Ray安装配置指南06BongoCat - 跨平台键盘猫动画工具07智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践08Labelme从安装到标注：零基础完整指南09《大数据技术原理与应用》实验报告三 熟悉HBase常用操作10NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南