前端自适应动态架构图演进

背景

随着业务增长，众多微服务依赖组成的架构，服务依赖关系过于复杂、不合理依赖、服务调用链过长、无效调用，环状调用等。保障、重构、治理都严重依赖人工进行梳理，没有全面的数据支撑，成本较高。

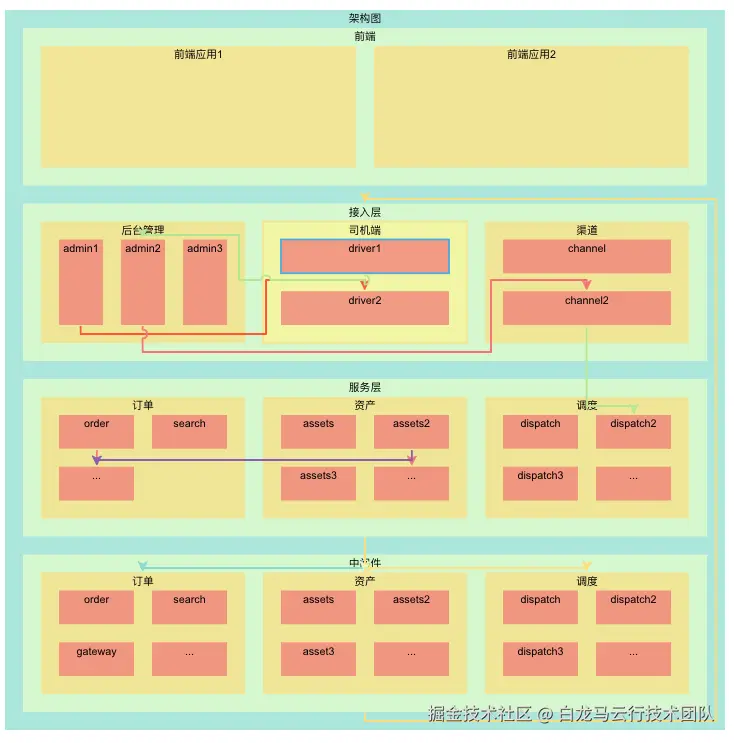
故急需一种可视化工具能力，将前后端调用链路数据生成全链路动态调用关系图，直观展示前后端服务间的组织结构、依赖和调用路径。

技术难点

最大的技术难点在于如何将非线性的树状层级结构 ，高效、清晰、美观地映射到二维的矩形平面上，并在此过程中保持数据的可读性、交互的流畅性以及视觉的合理性，同时还要适应不同屏幕尺寸。

1. 数据处理与算法难点

这是最核心的挑战，直接决定了Treemap的布局是否合理。

• 算法选择与适配： 传统的Treemap算法主要为展示文件目录（叶子节点有权重，中间节点权重为子节点之和）而设计，在架构图中， "权重"的定义变得复杂。
• 层级深度与宽度的平衡： 架构的层级可能很深（例如：全局 > 服务端 > 业务服务/接入层 > 业务线/非业务线 > 客服服务端 > 服务），也可能很宽（一个业务下可能有几十个服务）。深层级会导致矩形被切割得非常细小（"纸条化"），难以查看和交互。宽层级则可能导致矩形过于扁平，浪费空间。

2. 可视化与渲染难点

如何将算法计算出的布局数据转化为用户能理解的图形

• 自适应与响应式布局： "自适应"要求Treemap能随着容器（浏览器窗口、弹窗）大小的变化而动态重新计算布局并重绘。
• 视觉编码与美学： 如何用颜色、边框、标签等元素有效传递信息，比如不同层级、不同服务类型、状态；矩形可能很小，无法容纳长文本（如完整的服务名）；如何合理的间距（Padding）可以清晰地区分层级

矩形树图算法对比

传统矩形树图算法，通过将父节点划分为若干矩形区域，每个矩形的面积大小代表数据的数值权重（如数量、比例、大小等），而其内部矩形则表示子节点层级。

比如G2 Plot 矩形树图布局算法基于 d3-hierarchy 中的treemapBinary算法，echarts采用的是treemapSquarify算法

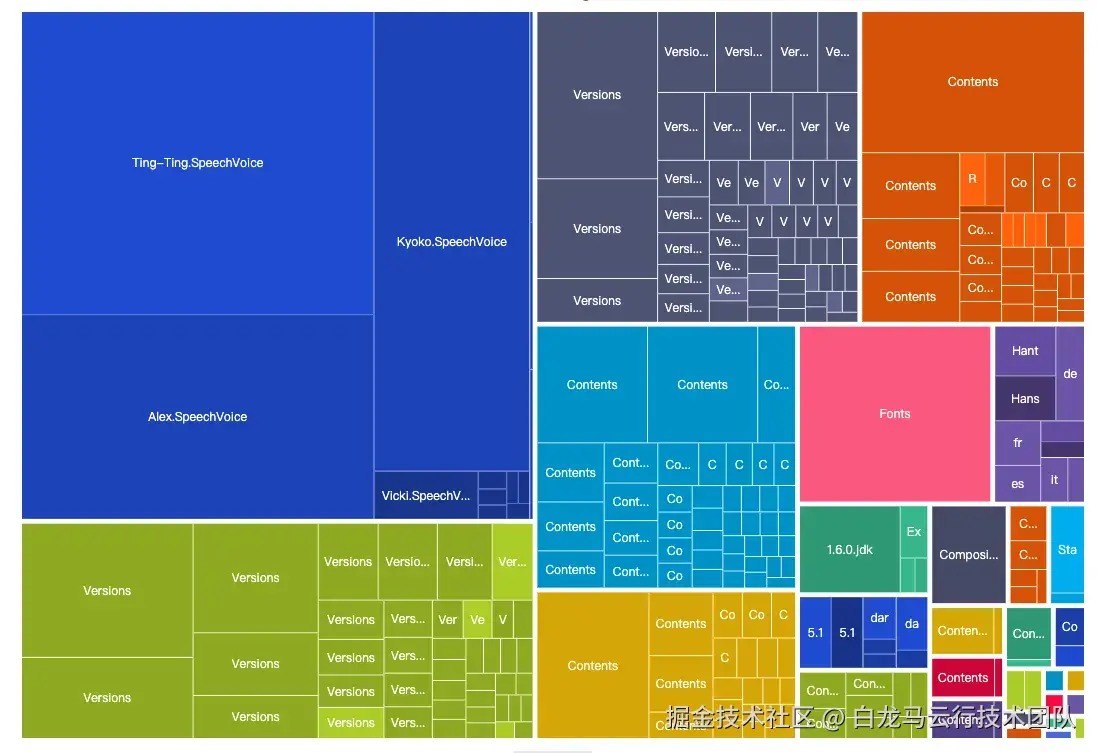以下为d3-hierarchy提供的treemap矩形树图算法：

对比维度	自适应矩形树关系图	treemapSlice	treemapDice	treemapSliceDice	treemapBinary	treemapSquarify
长宽比优化	良好	差	差	一般	良好	优
稳定性（节点顺序不乱）	稳定	稳定	稳定	稳定	一般	一般
视觉美观度	优	较差（细长条）	较差	一般	良好	优
计算复杂度	O(n)	O(n)	O(n)	O(n)	O(n log n)	O(n log n)
动态数据适应性	优	一般	一般	一般	一般	较差
实现思路	深度优先遍历计算权重，基于节点权重矩阵实现布局自适应宽高	单方向比例分配	垂直比例分配	两方向交替	面积二分递归	基于长宽比迭代优化
适用场景	分层架构图	层级结构展示	层级结构展示	文件结构展示、树形目录	实时数据展示、更新频繁场景	通用高美观图表

自适应矩形树关系图，相比传统矩形树图算法，还有如下优点：

1）支持多行多列网格布局

2）较小节点不会被隐藏展示，支持全量展示

3）架构层次清晰，支持多层嵌套

4）支持节点间关系线绘制

技术实现

设计原型（第一阶段）

矩形主关系图是由x6网格布局+嵌套布局为基础探索实现方案的原型方案，该布局实现了多行多列节点渲染

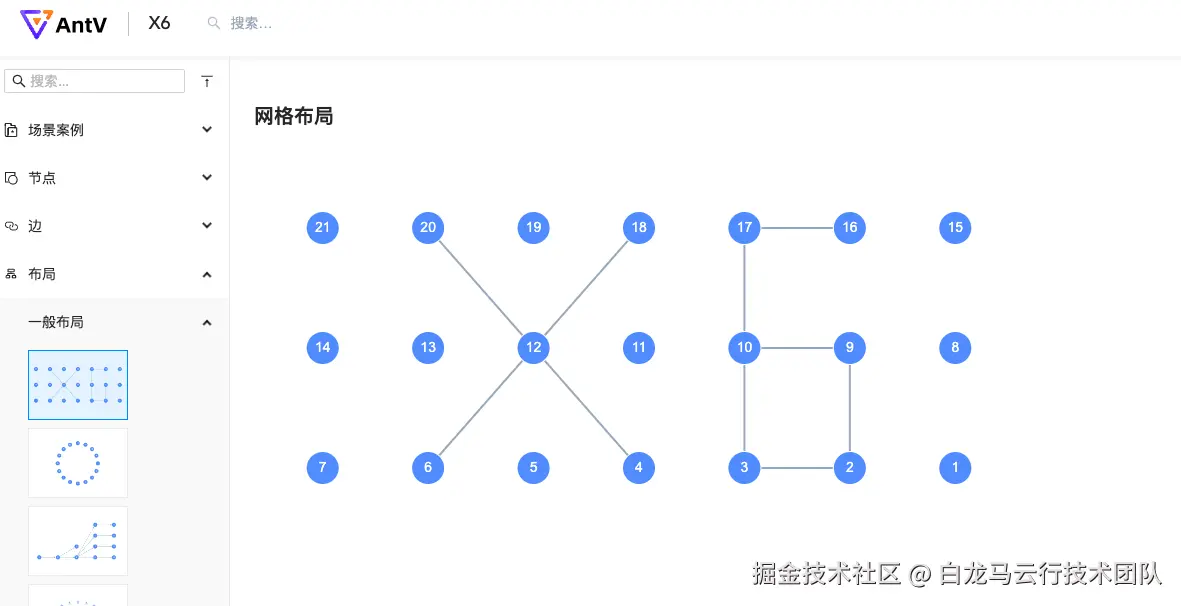
示例：

实现算法：

1. 循环节点列表，按照配置的cols列数和rows行数，初始化每个节点节点col、row配置信息
2. 根据节点的col和row和起点x轴y轴坐标计算每个节点的位置信息

  // 循环节点列表，按照配置的cols列数和rows行数，初始化每个节点节点col、row配置信息
  const cols = rcs.cols || 5;
  rc.col++;
  if (rc.col >= cols) {
    rc.col = 0;
    rc.row++;
  }
};

const getPos = (
  node: OutNode,
  begin: PointTuple,
  cellWidth: number,
  cellHeight: number,
  id2manPos: IdMapRowAndCol,
  rcs: RowsAndCols,
  rc: RowAndCol,
  cellUsed: VisitMap,
) => {
  let x: number;
  let y: number;

  // see if we have a manual position set
  const rcPos = id2manPos[node.id];
  if (rcPos) {
    // 首个节点配置，根据节点的col和row和起点x轴y轴坐标计算每个节点的位置信息
    x = rcPos.col * cellWidth + cellWidth / 2 + begin[0];
    y = rcPos.row * cellHeight + cellHeight / 2 + begin[1];
  } else {
    // otherwise set automatically

    while (used(cellUsed, rc)) {
      moveToNextCell(rcs, rc);
    }

    // 根据节点的col和row和起点x轴y轴坐标计算每个节点的位置信息
    x = rc.col * cellWidth + cellWidth / 2 + begin[0];
    y = rc.row * cellHeight + cellHeight / 2 + begin[1];
    use(cellUsed, rc);

    moveToNextCell(rcs, rc);
  }
  node.data.x = x;
  node.data.y = y;
};

不足：

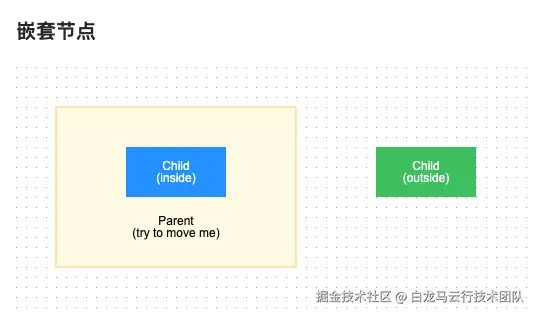
1. 网格布局只支持平均宽高布局，架构图多层嵌套且每一层节点数不统一时，布局分配松散不紧凑，空档较多
2. 嵌套节点未提供树形多级节点布局能力

自动扩展矩形树关系图（第二阶段）

该模型基于网格布局升级，以叶子节点基础向上计算生成紧凑矩形关系树，不仅支持多行多列布局，并且支持以下特性

• 多级树形结构节点嵌套
• 关系线躲避绘制
• 关系线多颜色绘制
• 关系线高亮
• 节点高亮
• 节点双击后限制该节点相关关系线，其余节点自动隐藏
• 支持自定义宽高
• 支持自定义行列树配置
• 根据节点自动向右向下扩展渲染

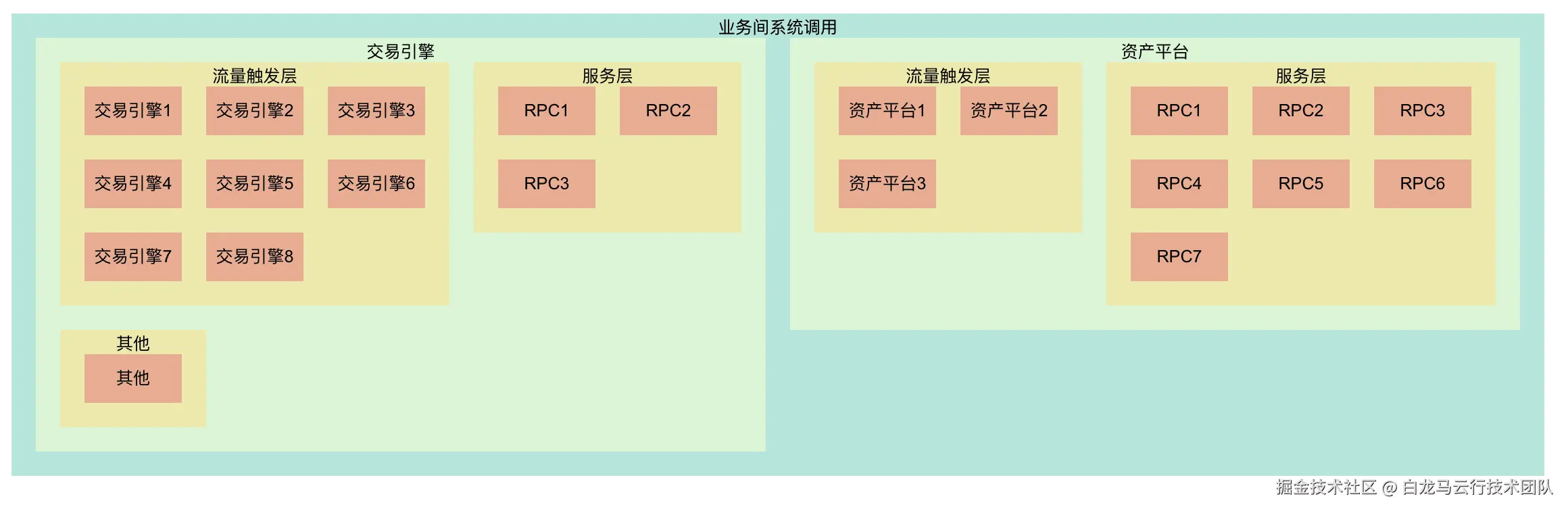
实现算法：

1. 广度优先遍历树形节点，补充节点属性visible是否显示、parentId父节点id

  const isLeaf = isLeafNode(node);
  if (!isLeaf) {
    node.attrs = node.attrs || {};
    node.attrs.collapsed =
      parent?.attrs?.collapsed || (typeof node.defaultCollapsed !== 'undefined' ? node.defaultCollapsed : false);
  }
  node.visible = !((isLeaf && parent?.attrs?.collapsed) || parent?.attrs?.collapsed);
  node.parentId = parent?.id;
  if ('children' in node) {
    node.children = node.children?.map((child) => addProperties(child, node));
  }
  return node;
};

2. 深度优先遍历树形节点，从末级节点开始计算父节点宽高

• 先序深度优先遍历节点计算节点左上角节点坐标

  • 节点左上角顶点x轴坐标：
    • 首列节点x轴坐标 = 父节点x轴坐标 + padding
    • 非首列节点x轴坐标 = 上一节点x轴坐标 + 上一节点节点宽度 + padding
  • 节点左上角顶点y轴坐标：
    • 首行节点y轴坐标 = 父节点y轴坐标 + padding
    • 非首行节点y轴坐标 = 上一行y轴最大坐标 + padding
  • 节点zIndex为父节点zIndex + 1

• 后序深度优先遍历节点，计算节点宽高
  • 叶子节点宽高计算
    • 宽度计算：如果当前节点有配置defaultWidth，则取defaultWidth，否则取常量minLeafWidth
    • 高度计算：如果当前节点有配置defaultHeight，则取defaultHeight，否则取常量minLeafHeight
  • 非叶子节点宽高计算

    • 宽度计算：如果当前节点有配置defaultWidth，则取defaultWidth，否则为所有子节点的最右侧x轴坐标 - 当前节点左上角顶点x轴坐标 + padding

      • 所有子节点的最右侧x轴坐标计算
        • 所有子节点的最右侧x轴坐标maxRight默认为0
        • 如果为首行，当前行x轴最大坐标 maxRowRight[rowIndex] = 当前节点x轴坐标 + 当前节点宽度
        • 如果非首行，当前行x轴最大坐标 maxRowRight[rowIndex] = Math.max(上一行x轴最大坐标, 当前节点x轴坐标 + 当前节点宽度）
        • 逐行比较，获取所有子节点最右侧x轴坐标maxRight = Math.max(maxRight，maxRowRight[rowIndex]）

    • 高度计算：如果当前节点有配置defaultHeight，则取defaultHeight，否则为所有子节点的最下方y轴坐标 - 当前节点左上角顶点y轴坐标 + padding

      • 所有子节点的最下方y轴坐标
        • 所有子节点的最下方y轴坐标maxBottom默认为0
        • 当前行每个节点y轴坐标为childRectY + childHeight，循环每一行，获取当前行最大y轴坐标为maxRowBottom[rowIndex] = Math.max(maxRowBottom[rowIndex] || 0, childRectY + childHeight);
        • 所有子节点的最下方y轴坐标maxBottom = 最后一行y轴最大坐标maxRowBottom[rowIndex]

  var cols = node.cols || node?.children?.length || 1;
  const curNodeX = (node.x = params.x);
  const curNodeY = (node.y = params.y);

  // 单行y轴最大坐标
  let maxRowBottom = {};
  // 单行x轴最大坐标
  let maxRowRight = {};
  // 最大y轴坐标
  let maxBottom = 0;
  // 最大x轴坐标
  let maxRight = 0;

  if ('children' in node) {
    node.children = node.children.reduce((acc, cur, index) => {
      // 当前节点行序号
      const rowIndex = Math.floor(index / cols);
      // 当前节点列序号
      const colIndex = index % cols;
      // 上一节点
      
      const preNode = acc[acc.length - 1];
      // 当前节点左上角顶点x轴坐标：
      // 		首列节点x轴坐标 = 父节点x轴坐标 + padding
      // 		非首列节点x轴坐标 = 上一节点x轴坐标 + 上一节点节点宽度 + padding
      const childRectX = colIndex ? preNode.x + preNode.width + padding : curNodeX + padding;
      // 当前节点左上角顶点y轴坐标
      // 		首行节点y轴坐标 = 父节点y轴坐标 + padding
      // 		非首行节点y轴坐标 = 上一行y轴最大坐标 + padding
      const childRectY = rowIndex ? maxRowBottom[rowIndex - 1] + padding : curNodeY + padding + 10; // +10避开关系线

      const childNode = layoutTraverse(
        cur,
        {
          x: childRectX,
          y: childRectY,
          zIndex: params.zIndex + 1,
        },
        node,
      );

      const childWidth = childNode.width;
      const childHeight = childNode.height;

      // 当前行下边沿
      maxRowBottom[rowIndex] = Math.max(maxRowBottom[rowIndex] || 0, childRectY + childHeight);
      // 总最下边沿
      maxBottom = maxRowBottom[rowIndex];

      // 当前行右边沿
      maxRowRight[rowIndex] = rowIndex
        ? Math.max(maxRowRight[rowIndex - 1] || 0, childRectX + childWidth)
        : childRectX + childWidth;
      // 总右边沿
      maxRight = Math.max(maxRight, maxRowRight[rowIndex]);
      acc.push(childNode);
      return acc;
    }, []);
  }

  let defaultWidth = node.defaultWidth || 0;
  if (isLeafNode(node) || (node?.attrs?.collapsed && (!parentNode || !parentNode?.attrs?.collapsed))) {
    node = setNode(node, {
      ...params,
      width: Math.max(defaultWidth, minLeafWidth),
      height: Math.max(node.defaultHeight || 0, minLeafHeight),
      isLeaf: true,
    });
  } else {
    node = setNode(node, {
      ...params,
      width: Math.max(defaultWidth, minLeafWidth, maxRight - curNodeX + padding),
      height: Math.max(node.defaultHeight || 0, minLeafHeight, maxBottom - curNodeY + padding),
      isLeaf: false,
    });
  }
  return node;
}

不足：

• 布局格式化过度依赖自定义配置，比如行列配置、自定义宽高等，如果出现节点增减，会出现布局错乱，需要修改自定义配置干预
• 在节点数目不固定，层级不固定时，布局相对较为错乱，且无有效规避手段
• 最大显示数依赖外部数据加工，导致筛选时不能筛选出被省略的节点

自适应矩形树关系图（第三阶段）

自适应矩形树关系图在自动扩展矩形树关系图基础上增加了节点自适应宽高填充，改进了矩形图节点坐标和宽高计算逻辑，基于节点权重矩阵实现布局自适应宽高，以适应各种不均匀数据结构展示。除此之外，支持以下功能：

• 节点右上角自定义标签，数字圆框和文字类型方框
• 节点宽高调整
• 节点位置调整
• 节点位置移动限制在父级节点范围内
• 节点属性设置支持多级配置

实现算法：

1. 增加节点行列配置

   • 广度优先遍历节点树

   • 如果当前节点有rows配置，根据rows配置计算当前节点cols配置： node.cols = Math.ceil(node.children.length / node.rows);

   • 如果当前节点有cols配置，根据cols配置计算当前节点rows配置
     node.rows = Math.ceil(length /node.cols);

   • 其他情况，根据平方函数计算行高列数
     const length = node.children.length;
const sqrt = Math.ceil(Math.sqrt(length));
node.cols = sqrt;
node.rows = Math.ceil(length / sqrt);

   • 继续遍历子节点

2. 计算节点权重

• 深度优先遍历树形节点

• 计算当前节点x轴权重

  • 如果当前节点不为子节点

    • 统计子节点x轴权重xWeight按照行列布局的矩阵xWeightMatrix，
    • 统计子节点权重矩阵xWeightMatrix每一行之和最大值maxRowSum
    • 因padding间距误差，需要增加间距误差权重数据

  • 如果当前节点为子节点

  • x轴权重xWeight为1

• 计算当前节点y轴权重

  • 如果当前节点不为子节点
    • 统计子节点x轴权重yWeight按照行列布局的矩阵yWeightMatrix，
    • 统计子节点权重矩阵yWeightMatrix每一行最大值求和sumOfMaxValues
    • 因padding间距误差，需要增加间距误差权重数据
  • 如果当前节点为子节点
    • x轴权重yWeight为1

• 计算当前节点最小宽度

  • 如果当前节点不为子节点
    • 统计子节点宽度按照行列布局的矩阵minWidthMatrix，
    • 统计子节点权重矩阵minWidthMatrix每一行最大值求和sumOfMaxValues
    • 因padding间距误差，需要增加间距误差权重数据
  • 如果当前节点为子节点
    • 最小宽度为minLeafWidth

• 计算当前节点最小高度

  • 如果当前节点不为子节点
    • 统计子节点高度minHeight按照行列布局的矩阵minHeightMatrix，
    • 统计子节点权重矩阵yWeightMatrix每一行最大值求和sumOfMaxValues
    • 因padding间距误差，需要增加间距误差权重数据
  • 如果当前节点为子节点
    • 最小高度为minLeafHeight

• 返回父节点，继续遍历

3. 计算节点布局（节点位置、宽高）
   • 计算全局子节点x轴权重矩阵、子节点y轴权重矩阵、x轴权重、y轴权重、最小宽度、最小高度
   • 广度优先遍历树形节点，透传a步骤数据
   • 计算节点左上角x轴坐标
     • 如果为第一列，取父节点x坐标+padding间距
     • 如果不为第一列，取上一节点x轴坐标+上一节点宽度+padding间距
   • 计算节点左上角y轴坐标
     • 如果为第一行，取父节点y坐标+padding间距
     • 如果不为第一行，且为第一列，取上一节点y轴坐标+上一节点高度+padding间距
     • 如果不为第一行且不为第一列，取上一节点y轴坐标
   • 计算节点宽度
     • 计算x轴每行总权重xWeightTotal
     • 权重比例为当前节点选中/x轴总权重xWeightTotal
     • 如果节点为有多行，且最后一行不足列数，父节点宽度减去最后一行列数权重比例
     • 其他情况，父节点宽度减去（列数 + 1）间距*权重比例
   • 计算节点高度
     • 计算y轴每一行权重最大值列表
     • 计算y轴权重最大值列表之和
     • 权重比例为每一行权重最大值/权重最大值列表之和
     • 高度减去（行数+1）间距*权重比例
   • 更新节点信息，继续遍历子节点

export const layoutTreemap = <T>(
  data,
  options: ITreeMapOptions = {},
  customNodeOptions: ICustomNodeOptionItem[] = [],
  hooks?: HooksFns<T>,
) => {
  let treeNodes = _.cloneDeep(data);
  const transData = compose(addLayout(options), addWeight, addProperties, modifyOptions(customNodeOptions));
  treeNodes = transData(treeNodes, hooks);
  return treeNodes;
};

// 增加节点行列配置
const addProperties = (treeNodes: INodeInfo[], parentNode?: INodeInfo) => {
  if (arrayNonEmpty(treeNodes)) {
    treeNodes = treeNodes.map((node) => {
      node.labels =
        parentNode?.labels && parentNode?.labels.length > 0 ? [...parentNode.labels, node.label] : [node.label];

      if (arrayNonEmpty(node.children)) {
        if (node.rows) {
          const length = node.children.length;
          node.cols = Math.ceil(length / node.rows);
          node.rows = length < node.rows ? length : node.rows;
        } else if (node.cols) {
          const length = node.children.length;
          node.cols = length < node.cols ? length : node.cols;
          node.rows = Math.ceil(length / node.cols);
        } else {
          const length = node.children.length;
          const sqrt = Math.ceil(Math.sqrt(length));
          node.cols = sqrt;
          node.rows = Math.ceil(length / sqrt);
        }
        node.isLeaf = false;
        node.children = addProperties(node.children, node);
      } else {
        node.isLeaf = true;
      }
      node.parentId = parentNode?.id;
      node.visible = true;

      return node;
    });
  }
  return treeNodes;
};

// 计算节点权重
const calcWithPadding = (n) => (data) => (n + 1) * padding + data;
// 解决因padding导致的权重计算误差
const calcWeightWithPadding = (n, min) => (data) => ((n + 1) * padding) / min + data;
const addWeight = (treeNodes) => {
  if (arrayNonEmpty(treeNodes)) {
    treeNodes = treeNodes.map((node) => {
      if (arrayNonEmpty(node.children)) {
        node.children = addWeight(node.children);
        node = updatePorpertyByMatrix(node, 'xWeight', [calcWeightWithPadding(node.cols, minLeafWidth), getMaxRowSum]);
        node = updatePorpertyByMatrix(node, 'yWeight', [
          calcWeightWithPadding(node.rows, minLeafHeight),
          getSumOfMaxInRows,
        ]);
        node = updatePorpertyByMatrix(node, 'minWidth', [calcWithPadding(node.cols), getMaxRowSum]);
        node = updatePorpertyByMatrix(node, 'minHeight', [calcWithPadding(node.rows), getSumOfMaxInRows]);
      } else {
        node.xWeight = node.xWeight || 1;
        node.yWeight = node.yWeight || 1;
        node.minWidth = node.minWidth || minLeafWidth;
        node.minHeight = node.minHeight || minLeafHeight;
      }
      return node;
    });
  }
  return treeNodes;
};

// 计算节点布局（节点位置、宽高）
const addLayout =
  (options: ITreeMapOptions = {}) =>
  (treeNodes) => {
    const traverseLayout = (treeNodes, params) => {
      const { x: curNodeX, y: curNodeY, width, height, rows, cols, xWeightMatrix, yWeightMatrix, zIndex } = params;

      if (arrayNonEmpty(treeNodes)) {
        treeNodes = treeNodes.reduce((acc, cur, index) => {
          const rowIndex = Math.floor(index / cols);
          const colIndex = index % cols;
          const preNode = acc[acc.length - 1];
          const childRectX = colIndex ? preNode.x + preNode.width + padding : curNodeX + padding;
          let childRectY = 0;
          if (rowIndex === 0) {
            childRectY = curNodeY + padding;
          } else if (colIndex === 0) {
            childRectY = preNode.y + preNode.height + padding;
          } else {
            childRectY = preNode.y;
          }
          const xWeightTotal = xWeightMatrix[rowIndex].reduce((sum, value) => sum + value, 0);
          // 使用 map 计算每一行的最大值
          const maxValues = yWeightMatrix.map((row) => Math.max(...row));
          const yWeightTotal = maxValues.reduce((sum, value) => sum + value, 0);
          const childWidth =
            rowIndex === rows - 1 && treeNodes.length % cols !== 0 && treeNodes.length > cols
              ? (width - ((treeNodes.length % cols) + 1) * padding) * (cur.xWeight / xWeightTotal)
              : Math.floor((width - (cols + 1) * padding) * (cur.xWeight / xWeightTotal));
          // 因部分节点未达到最大权重，而需要去除padding后按照实际权重平分
          const childHeight = Math.floor((height - (rows + 1) * padding) * (maxValues[rowIndex] / yWeightTotal));

          cur = setNode(cur, {
            x: childRectX,
            y: childRectY,
            width: childWidth,
            height: childHeight,
            zIndex: zIndex + 1,
          });

          if (arrayNonEmpty(cur.children)) {
            cur.children = traverseLayout(cur.children, cur);
          }
          acc.push(cur);
          return acc;
        }, []);
      }
      return treeNodes;
    };

    const xWeightMatrix = getMatrix(treeNodes, 1, treeNodes.length, (child) => child.xWeight);
    const yWeightMatrix = getMatrix(treeNodes, 1, treeNodes.length, (child) => child.yWeight);
    const xWeight = calcWeightWithPadding(treeNodes.length, minLeafWidth)(getMaxRowSum(xWeightMatrix));
    const yWeight = calcWeightWithPadding(1, minLeafHeight)(getSumOfMaxInRows(yWeightMatrix));
    const minWidth =
      treeNodes.map((node) => node.minWidth).reduce((acc, cur) => acc + cur, 0) + (treeNodes.length + 1) * padding;
    const minHeight = Math.max(treeNodes.map((node) => node.minHeight)) + 2 * padding;

    treeNodes = traverseLayout(treeNodes, {
      x: 0,
      y: 0,
      ...options,
      width: !options.width || minWidth > options.width ? minWidth : options.width,
      height: !options.height || minHeight > options.height ? minHeight : options.height,
      rows: 1,
      cols: treeNodes.length,
      xWeightMatrix,
      yWeightMatrix,
      xWeight,
      yWeight,
      zIndex: 0,
    });

    return treeNodes;
  };

落地结果&收益

• 业务价值

  • 架构可视化与全局洞察 ：将原本存在于文档、代码或PPT中的静态、抽象的架构描述，转化为一个动态、交互、可感知 的视觉系统。无论是新老员工，5 分钟内掌握系统整体结构与规模，降低了架构的理解门槛和沟通成本
  • 服务治理与健康状态监控： 架构图上服务节点实时渲染不同服务健康状态，10s 内 发现系统薄弱环节和异常节点，减少人工巡检频次，整体运维效率提升 40%+ ， 实现监控的可视化运维
  • 依赖关系与影响分析： 基于服务架构图，实现直观展示服务间的调用链和依赖关系，架构变更或故障排查时查找依赖上下游，一键定位依赖链路，平均定位问题耗时由小时级降至 分钟级（≤5min）

• 技术价值

  • 树形分层结构均匀渲染，空间利用率高，节点之间的交叉重叠率为 0 ，填充率 （子节点面积之和/父节点面积，内边距除外）为 1 ，空隙率 （未被任何节点占用的空间比例）为 0
  • 支持多层嵌套，1000+ 节点 7 层嵌套，布局平均耗时 635ms ，时间复杂度为 O(n)

结语

在微服务架构逐渐成为主流的今天，服务依赖关系的复杂性已经成为许多技术团队面临的共同挑战。本文探讨的可视化解决方案，通过树形结构节点遍历算法，配合基于节点权重的自适应布局计算，为复杂的服务调用关系提供了直观的展现方式。

这个实现不仅解决了服务依赖可视化的问题，更重要的是为架构治理提供了数据支撑。通过动态生成的调用关系图，团队可以快速识别架构设计不合理等潜在问题，使架构优化工作有的放矢。

技术实现上，我们特别注重了以下几点：

1. 算法效率与可视化性能的平衡

2. 不均匀数据结构的自适应展现

3. 节点权重矩阵的动态计算

4. 布局算法的可扩展性

未来，这个工具还可以进一步扩展，比如加入实时监控数据、性能指标叠加、智能告警等功能，使其成为微服务治理的综合性平台。

架构可视化不是终点，而是持续优化的起点。希望这个方案能够帮助更多团队驾驭复杂的微服务架构，让技术架构真正成为业务发展的助推器而非瓶颈。