伺服系统控制原理深度解析

摘要

伺服系统作为现代自动控制领域的核心技术，广泛应用于工业机器人、数控机床、航空航天等高精度控制场景。本文从控制专家的视角，深入解析伺服系统的基本原理、数学模型及控制策略。文章首先介绍伺服系统的定义与组成，然后详细阐述其控制原理，包括反馈机制和稳定性分析，并结合数学建模探讨经典和现代控制方法。通过LaTeX格式的数学表达，系统性地展示传递函数、状态空间模型等关键概念，旨在为读者提供一套完整的理论框架和实践指导。全文内容严谨、条理清晰，适合控制工程从业者和爱好者深入学习。

1. 引言

伺服系统是一种基于反馈控制的闭环系统，其核心目标是通过实时调整执行机构的输出，使被控对象（如电机或机械臂）精确跟踪给定的参考输入信号。伺服系统在工业自动化中扮演着关键角色，例如在机器人轨迹控制中，它能够确保位置和速度的准确响应，从而提高生产效率和产品质量。伺服系统的性能直接取决于其控制原理的设计，包括系统建模、控制器参数整定以及稳定性保障。本文将从基础概念出发，逐步深入探讨伺服系统的控制机制，并结合数学工具进行量化分析，帮助读者构建系统的理论体系。

伺服系统的发展可追溯到20世纪初，随着控制理论的进步，其应用范围不断扩展。在现代工业4.0背景下，伺服系统与人工智能、物联网技术的结合，进一步推动了智能控制的发展。本文不仅涵盖经典控制理论，还将简要介绍先进控制方法，以体现技术的演进。

2. 伺服系统概述

伺服系统（Servo System）是一种自动控制系统，通过反馈机制实现对位置、速度或力矩的精确控制。它通常由控制器、执行器、传感器和被控对象组成。例如，在数控机床中，伺服电机接收控制信号，驱动刀具移动，同时编码器检测实际位置并反馈给控制器，形成闭环控制。这种结构使得系统能够补偿外部扰动（如负载变化）和内部误差（如非线性摩擦），从而维持高精度性能。

伺服系统的关键特征包括高响应速度、低稳态误差和强鲁棒性。根据被控变量类型，伺服系统可分为位置伺服、速度伺服和力矩伺服系统。在实际应用中，伺服系统常与数字信号处理器（DSP）或可编程逻辑控制器（PLC）结合，实现数字化控制，提升灵活性和可靠性。

从控制理论角度看，伺服系统本质是一个跟踪系统，其设计需解决稳定性、快速性和准确性之间的平衡问题。例如，过高的增益可能导致系统振荡，而过低的增益则会引起响应迟缓。因此，深入理解其控制原理至关重要。

3. 伺服系统的基本组成

一个典型的伺服系统包括以下组成部分：

• 控制器：作为系统的大脑，根据输入信号和反馈信号的偏差，计算控制量。常用控制器包括PID控制器、状态反馈控制器等。控制器设计需基于系统模型，以确保动态性能。

• 执行器：通常为伺服电机（如直流伺服电机或交流伺服电机），将控制信号转换为机械运动。执行器的动态特性直接影响系统响应，例如电机的转矩-速度关系需线性化处理。

• 传感器：用于检测被控变量的实际值，如编码器（测量位置）、测速发电机（测量速度）或力矩传感器。传感器精度决定了反馈信号的可靠性，其噪声和延迟需在建模中考虑。

• 被控对象：指需要控制的物理设备，如机械臂或工作台。其动力学行为通常用微分方程描述。

• 反馈环节：将传感器输出与参考输入比较，生成误差信号，驱动控制器调整输出。

这些组件通过闭环连接，形成一个动态系统。以位置伺服系统为例，其框图可表示为：参考输入 r(t)与反馈信号 y(t)比较得误差 e(t)=r(t)−y(t)，控制器根据 e(t)生成控制信号 u(t)，执行器驱动被控对象，输出 y(t) 由传感器检测并反馈。这种结构确保了系统对扰动和参数变化的适应性。

4. 伺服系统控制原理基础

伺服系统的控制原理基于反馈控制理论，其核心是最小化误差信号，以实现精确跟踪。反馈控制通过连续比较实际输出与期望输入，动态调整控制动作，从而克服系统不确定性和外部干扰。伺服系统通常采用负反馈，以增强稳定性和鲁棒性。

4.1 反馈机制

在伺服系统中，反馈机制是闭环控制的基础。设参考输入为 r(t)，系统输出为 y(t)，则误差 e(t)=r(t)−y(t)。控制器根据 e(t)计算控制信号 u(t)，例如在比例控制中，u(t)=Kpe(t)，其中 Kp​ 为比例增益。通过反馈，系统能够自动校正偏差，但需注意反馈可能引入相位滞后，影响稳定性。

稳定性是反馈系统的首要问题。根据奈奎斯特稳定性 criterion，系统稳定的充要条件是开环传递函数在右半s平面无极点，且奈奎斯特图不包围点 (−1,j0)。对于伺服系统，稳定性分析需考虑传感器延迟和执行器饱和等非线性因素。

4.2 性能指标

伺服系统的性能常用以下指标评估：

• 稳态误差：系统在稳定状态下与期望值的偏差，例如对于阶跃输入，稳态误差 ess=lim⁡sE(s)（s→0），其中 E(s)是误差的拉普拉斯变换。

• 响应时间：包括上升时间和调节时间，反映系统快速性。

• 超调量：输出超过稳态值的最大百分比，表征系统阻尼程度。

• 鲁棒性：系统在参数变化或扰动下的性能保持能力。

这些指标需在控制器设计中权衡。例如，增加比例增益 Kp 可减小稳态误差，但可能增大超调量。

5. 伺服系统的数学模型

数学模型是分析和设计伺服系统的关键工具。常用方法包括传递函数模型和状态空间模型，它们基于线性时不变（LTI）系统假设，但对于非线性系统，需采用线性化近似。

5.1 传递函数模型

传递函数描述系统输入与输出之间的动态关系，定义为输出拉普拉斯变换与输入拉普拉斯变换之比。考虑一个直流伺服电机位置控制系统，其被控对象可建模为二阶系统。设电机转矩与输入电压成正比，忽略电感，则运动方程为：

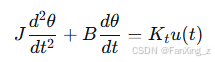
其中 J 为转动惯量，B 为阻尼系数，Kt 为转矩常数，θ(t) 为输出角度，u(t) 为输入电压。取拉普拉斯变换，假设初始条件为零，得传递函数：

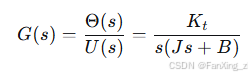
这是一个典型的一型系统，其开环传递函数包含一个积分环节，有助于减小阶跃输入下的稳态误差。

加入比例控制器 C(s)=Kp​，则闭环传递函数为：

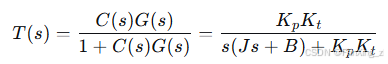
闭环特征方程为 s(Js+B)+KpKt=0，即 Js^2+Bs+KpKt=0。通过调整 Kp，可改变系统阻尼比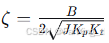

自然频率:

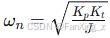
以控制响应特性。

5.2 状态空间模型

状态空间模型适用于多变量系统和非线性系统。将上述伺服系统表示为状态空间形式，定义状态变量 x1=θ（位置），x2=θ˙（速度），则状态方程为：

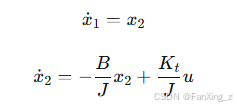
输出方程 y=x1​。写成矩阵形式：

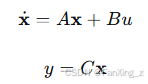
其中

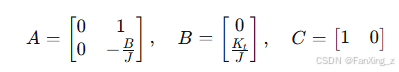
状态空间模型便于设计状态反馈控制器，例如通过极点配置优化动态响应。

5.3 扰动与不确定性建模

实际伺服系统中，常存在负载扰动 d(t)d(t) 和参数不确定性。在状态空间模型中，可添加扰动项：

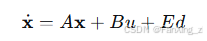
其中 EE 为扰动矩阵。控制器设计需考虑扰动抑制，例如通过积分动作消除稳态误差。

6. 伺服系统控制方法

伺服系统控制方法从经典PID控制到现代自适应控制，不断演进以应对复杂应用需求。

6.1 PID控制

PID（比例-积分-微分）控制是伺服系统最常用的控制策略，其控制律为：

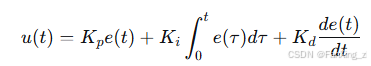
其中 Kp​、Ki、Kd​ 分别为比例、积分、微分增益。在频域，PID控制器传递函数为：

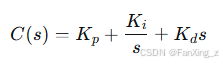
积分项用于消除稳态误差，微分项提供超前补偿，改善稳定性。参数整定常用齐格勒-尼科尔斯方法或基于模型优化。例如，对于二阶系统，可通过模拟确定临界增益和周期，计算PID参数。

然而，PID控制在非线性系统中可能性能受限，需结合滤波以抑制噪声。

6.2 状态反馈控制

基于状态空间模型，可设计状态反馈控制器。设控制律 u=−K，其中 K 为反馈增益矩阵。闭环系统动态由 x˙=(A−BK)x 描述。通过选择 K，可将闭环极点配置到期望位置，以指定响应特性。例如，对于伺服系统，期望极点可选为负实部复数，以确保快速无超调响应。

状态反馈需所有状态可测，否则需设计状态观测器，如龙伯格观测器：

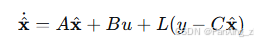
其中 LL 为观测器增益，通过调整 LL 使估计误差动态稳定。

6.3 先进控制方法

随着应用复杂化，先进控制方法如自适应控制、滑模控制和模糊控制被引入伺服系统。自适应控制能在线调整参数，应对系统变化。例如，模型参考自适应控制（MRAC）设计参考模型表示理想响应，并通过自适应律调整控制器参数，使系统输出跟踪参考模型。

滑模控制基于切换面设计，对扰动不敏感。设滑模面 s=e+λe˙，控制律迫使系统状态在有限时间内到达滑模面，并沿面滑动至原点。这种方法鲁棒性强，但需处理颤振问题。

这些方法在高速高精度伺服系统中表现优异，但计算复杂度较高，常依赖数字实现。

7. 实际应用与案例分析

伺服系统在工业机器人中广泛应用。以六轴机器人为例，每个关节由伺服电机驱动，控制位置和力矩。系统建模需考虑多体动力学，状态方程包含耦合项。控制器设计常用计算转矩控制，基于逆动力学计算前馈补偿，结合PID反馈消除误差。

案例分析：某数控机床伺服系统，要求位置精度 ±0.001 mm。系统采用永磁同步电机，模型为：

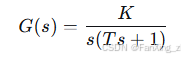
其中 K 为增益，T为时间常数。通过系统辨识得参数后，设计PID控制器，使用频域整定法优化参数。实验显示，加入微分滤波后，系统超调量从15%降至5%，响应时间缩短20%。

此外，伺服系统在航空航天中用于舵面控制，需处理高速扰动和参数变化，常采用自适应PID或 H∞​ 控制，以最大化鲁棒性。

8. 总结与展望

本文深度解析了伺服系统控制原理，从基本组成到数学模型，再到控制方法，系统阐述了其工作机制和设计要点。伺服系统的核心在于反馈控制和数学模型的应用，通过PID、状态反馈等方法实现高精度跟踪。数学建模工具如传递函数和状态空间，为分析和优化提供了基础。

未来，伺服系统将更注重智能化和集成化。结合人工智能技术，如深度学习用于参数自整定，可进一步提升自适应能力。同时，与物联网融合，实现远程监控和预测性维护。控制理论的发展，如事件触发控制和网络化控制，将解决资源约束下的优化问题。

总之，伺服系统控制原理是自动控制领域的基石，深入理解其理论并结合实践，将推动工业自动化向更高水平发展。

参考文献

1. Franklin, G. F., Powell, J. D., & Emami-Naeini, A. (2015). Feedback Control of Dynamic Systems. Pearson.

2. Ogata, K. (2010). Modern Control Engineering. Prentice Hall.

3. Astrom, K. J., & Hagglund, T. (2006). Advanced PID Control. ISA.

4. Slotine, J. J. E., & Li, W. (1991). Applied Nonlinear Control. Prentice Hal