【高级机器学习】 10. 领域适应与迁移学习

Domain Adaptation & Transfer Learning

一、问题引入：为什么训练集学到的模型能泛化？

我们希望学习到的假设 hSh_ShS 不仅在训练集上好用，也能在测试集上表现良好。

核心假设：

训练集与测试集来自相同的分布 P(X,Y)P(X,Y)P(X,Y)。于是训练误差（经验风险）RS(h)R_S(h)RS(h) 就是真实风险（期望风险）R(h)R(h)R(h) 的一个无偏估计。

R(h)=E(X,Y)∼P[ℓ(X,Y,h)]andRS(h)=1n∑i=1nℓ(Xi,Yi,h) R(h) = \mathbb{E}{(X,Y)\sim P}[\ell(X,Y,h)] \quad \text{and} \quad R_S(h) = \frac{1}{n}\sum{i=1}^{n}\ell(X_i, Y_i, h) R(h)=E(X,Y)∼P[ℓ(X,Y,h)]andRS(h)=n1i=1∑nℓ(Xi,Yi,h)

若样本足够大，RS(h)≈R(h)R_S(h)\approx R(h)RS(h)≈R(h)，因此模型在测试集上也会有相似的误差水平 。

这就是机器学习中"泛化能力"的根基。

二、过拟合（Overfitting）与泛化失败

定义：
RS(h) 小但R(h) 大. R_S(h)\ \text{小} \quad \text{但}\quad R(h)\ \text{大}. RS(h) 小但R(h) 大.

即模型在训练集上学得很好，却无法在未见过的数据上泛化。

原因：

模型容量过大；
训练集噪声；
正则化不足；
采样偏差（sampling bias）。

要点：

过拟合不是违反分布一致假设，而是由于有限样本和模型复杂度导致经验风险最小化与期望风险最小化不再一致。

三、数据分布（Data Distribution）

若两个任务的数据分布相同（同一总体），其训练样本在统计上也会相似；
若分布不同，则任务的性质不同，无法简单共用同一模型；
因此，"分布"是任务差异的根源。

一般结论：

如果两个任务共享相同的总体分布，可以使用相似的学习算法。

四、风险定义与符号（Notation）

期望风险（Expected Risk）

R(h)=E[ℓ(X,Y,h)]=∫ℓ(X,Y,h)p(X,Y) dX dY R(h) = \mathbb{E}[\ell(X,Y,h)] = \int \ell(X,Y,h)p(X,Y)\,dX\,dY R(h)=E[ℓ(X,Y,h)]=∫ℓ(X,Y,h)p(X,Y)dXdY

经验风险（Empirical Risk）

RS(h)=1n∑i=1nℓ(Xi,Yi,h) R_S(h) = \frac{1}{n}\sum_{i=1}^{n}\ell(X_i, Y_i, h) RS(h)=n1i=1∑nℓ(Xi,Yi,h)

最优函数定义

理想最优（target concept）
c=arg⁡min⁡hR(h) c = \arg\min_h R(h) c=arghminR(h)
假设空间内的最优
h∗=arg⁡min⁡h∈HR(h) h^* = \arg\min_{h\in H}R(h) h∗=argh∈HminR(h)
通过数据学习到的假设
hS=arg⁡min⁡h∈HRS(h) h_S = \arg\min_{h\in H} R_S(h) hS=argh∈HminRS(h)

hSh_ShS 是算法能实际学到的模型，期望 R(hS)R(h_S)R(hS) 接近 R(h∗)R(h^*)R(h∗)。

五、域（Domain）的定义

一个学习算法可以看作一个映射：
A:S∈(X×Y)n↦hS∈H \mathcal{A}: S \in (\mathcal{X}\times\mathcal{Y})^n \mapsto h_S \in H A:S∈(X×Y)n↦hS∈H

在机器学习中：

数据的输入分布（即 P(X)P(X)P(X) 或 (X,Y)(X,Y)(X,Y) 的联合分布）被称为 Domain（领域）。

不同的任务可能对应不同的 domain。

六、人类的知识迁移类比

人类能够在相似任务之间迁移经验 ：

例如羽毛球 ↔ 网球、国际象棋 ↔ 中国象棋。

虽然规则不同，但背后的策略、博弈逻辑相通。

思考：

机器能否像人一样发现领域间的共通知识并迁移？

七、人 vs 机器

Human	Machine
经验（Experience）	样本（Sample）
选择规则（Choose a rule）	选择假设（Choose a hypothesis）
做决策（Make a decision）	做预测（Do a prediction）

机器学习的目标之一：让机器像人类一样，通过已有知识适应新环境。

八、Domain Adaptation 与 Transfer Learning

机器同样可以在数据之间发现共通知识，从一个领域（source domain）迁移到另一个领域（target domain）。

这正是 领域自适应 (Domain Adaptation) 与 迁移学习 (Transfer Learning) 的核心。

在迁移学习中，我们利用源域的样本或模型知识，来提升目标域的性能。

九、总结与术语对照

Domain Adaptation（领域自适应）

目标：减少源域与目标域之间的分布差异；
方法：特征对齐、重加权、对抗学习、MMD等；
理想状态：源域和目标域在新特征空间下满足
Ps(X)≈Pt(X) P_s(X)\approx P_t(X) Ps(X)≈Pt(X)
一句话概括： 让两个域的分布看起来"像来自同一个世界"。

Transfer Learning（迁移学习）

目标：从源域中提取知识并应用到目标域；
方法：参数共享、预训练--微调、知识蒸馏、提示学习等；
效果：提升目标域上模型性能或训练效率；
一句话概括： 把学到的知识带到新领域，帮它学得更快、更好。

Transfer Learning（迁移学习）

目标：把在源域学到的"知识"搬到目标域 去用，从而更快/更好 地完成预测任务（给出特征 xxx，预测标签 yyy）。

1) 问题设定与符号

源域数据（带标签）
{(x1S,y1S),...,(xnSS,ynSS)}. \{(x_1^S,y_1^S),\ldots,(x_{n_S}^S,y_{n_S}^S)\}. {(x1S,y1S),...,(xnSS,ynSS)}.
目标域数据（常见情况是少量或无标签）
{(x1T,y1T),...,(xnTT,ynTT)}或{x1T,...,xnTT}. \{(x_1^T,y_1^T),\ldots,(x_{n_T}^T,y_{n_T}^T)\}\quad\text{或}\quad \{x_1^T,\ldots,x_{n_T}^T\}. {(x1T,y1T),...,(xnTT,ynTT)}或{x1T,...,xnTT}.
任务：学到一个模型 hhh，使得遇到任何特征 xxx 都能正确预测 yyy。

直观版 ：先在"旧世界"（源域）训练出 Model A ，把"有用的知识"抽出来，帮助"新世界"（目标域）的 Model B 学得更好。

2) 为什么要做迁移学习？

在很多领域里，数据尤其是标注数据非常贵 （例如真实道路上的自动驾驶）。

但在一些相关的领域里，大量标注数据却很容易获得（例如高仿真的驾驶模拟器）。

比喻：

你在"模拟考"里练了很多题（源域），就能更快学会"真正考试"的套路（目标域），哪怕真正考试题目有点不一样。

3) 关键挑战：分布变了，知识怎么转？

迁移前要搞清楚：不同域的联合分布 p(X,Y)p(X,Y)p(X,Y) 是怎么变的 。

只有知道"变在哪里"，我们才能决定转什么 、怎么转。

常见情形：

协变量漂移（Covariate shift） ：ps(X)≠pt(X)p_s(X)\neq p_t(X)ps(X)=pt(X)，但 ps(Y∣X)≈pt(Y∣X)p_s(Y|X)\approx p_t(Y|X)ps(Y∣X)≈pt(Y∣X)。

标签分布漂移（Label shift） ：ps(Y)≠pt(Y)p_s(Y)\neq p_t(Y)ps(Y)=pt(Y)，但 ps(X∣Y)≈pt(X∣Y)p_s(X|Y)\approx p_t(X|Y)ps(X∣Y)≈pt(X∣Y)。

一般分布差异 ：ps(X,Y)≠pt(X,Y)p_s(X,Y)\neq p_t(X,Y)ps(X,Y)=pt(X,Y)。

4) 重要性重加权（Importance Reweighting）：把"像目标域的样本"权重大一点

设目标域上的期望风险 为
RT(h)=E(X,Y)∼pt[ℓ(X,Y,h)]. R^T(h)=\mathbb{E}_{(X,Y)\sim p_t}[\ell(X,Y,h)]. RT(h)=E(X,Y)∼pt[ℓ(X,Y,h)].

对它做一步"代数换元"，把在目标域上的积分/期望，改写成在源域上的期望------但要乘上一个权重比率 ：
RT(h)=E(X,Y)∼pt[ℓ(X,Y,h)]=∫ℓ(X,Y,h) pt(X,Y) dX dY=∫ℓ(X,Y,h) pt(X,Y)ps(X,Y) ps(X,Y) dX dY=E(X,Y)∼ps ⁣[pt(X,Y)ps(X,Y)⏟β(X,Y) ℓ(X,Y,h)]=E(X,Y)∼ps[β(X,Y) ℓ(X,Y,h)]. \begin{aligned} R^T(h) &=\mathbb{E}{(X,Y)\sim p_t}[\ell(X,Y,h)] \\ &=\int \ell(X,Y,h)\,p_t(X,Y)\,dX\,dY \\ &=\int \ell(X,Y,h)\,\frac{p_t(X,Y)}{p_s(X,Y)}\,p_s(X,Y)\,dX\,dY \\ &=\mathbb{E}{(X,Y)\sim p_s}\!\left[\underbrace{\frac{p_t(X,Y)}{p_s(X,Y)}}{\displaystyle \beta(X,Y)}\,\ell(X,Y,h)\right] \\ &=\mathbb{E}{(X,Y)\sim p_s}\big[\beta(X,Y)\,\ell(X,Y,h)\big]. \end{aligned} RT(h)=E(X,Y)∼pt[ℓ(X,Y,h)]=∫ℓ(X,Y,h)pt(X,Y)dXdY=∫ℓ(X,Y,h)ps(X,Y)pt(X,Y)ps(X,Y)dXdY=E(X,Y)∼ps β(X,Y) ps(X,Y)pt(X,Y)ℓ(X,Y,h) =E(X,Y)∼ps[β(X,Y)ℓ(X,Y,h)].

这里的
β(X,Y)=pt(X,Y)ps(X,Y) \beta(X,Y)=\frac{p_t(X,Y)}{p_s(X,Y)} β(X,Y)=ps(X,Y)pt(X,Y)

就是重要性权重 ：表示在目标域里，这种样本相对源域来说有多重要。

5) 用源域样本近似目标域风险

如果我们能估计到 β(X,Y)\beta(X,Y)β(X,Y)，那么就可以用源域的样本来"模拟"目标域的期望风险：
RT(h)≈1nS∑i=1nSβ ⁣(xiS,yiS) ℓ ⁣(xiS,yiS,h). R^T(h)\approx \frac{1}{n_S}\sum_{i=1}^{n_S}\beta\!\big(x_i^S,y_i^S\big)\,\ell\!\big(x_i^S,y_i^S,h\big). RT(h)≈nS1i=1∑nSβ(xiS,yiS)ℓ(xiS,yiS,h).

于是，一个直接的训练策略是最小化上式 （在源域样本上做加权的经验风险最小化 ）：
h⋆ = arg⁡min⁡h 1nS∑i=1nSβ ⁣(xiS,yiS) ℓ ⁣(xiS,yiS,h). h^\star \;=\;\arg\min_h\;\frac{1}{n_S}\sum_{i=1}^{n_S}\beta\!\big(x_i^S,y_i^S\big)\,\ell\!\big(x_i^S,y_i^S,h\big). h⋆=arghminnS1i=1∑nSβ(xiS,yiS)ℓ(xiS,yiS,h).

类比：

做"加权的模拟题"。和目标考试更像的题目（样本）得分占比更大，你的总分就更接近真实考试的表现。

6) 迁移的"知识"可以是什么？

特征/表示 ：把 xxx 变成"更通用"的表征（如自监督/对比学习得到的表征），让 ps(X)≈pt(X)p_s(X)\approx p_t(X)ps(X)≈pt(X)。
参数/初始化 ：用源域训练好的网络当预训练权重 ，在目标域微调。
规则/结构：迁移网络模块、损失函数、数据增强策略等。
样本权重：像上面的重要性重加权，直接在损失里体现。

7) 实用贴士（避免"负迁移"）

估计 β\betaβ 要稳健：可用核密度/概率分类器比值/对抗学习（domain discriminator）等方式估计，注意平滑与截断，避免极端比值。
表示对齐：通过对抗式对齐、MMD、CORAL 等，让源/目标在新空间里更接近。
少量目标域监督很值钱：有标签的小批目标数据能显著稳定微调与对齐。
监控是否"越学越差"：一旦出现，降低迁移强度或改策略（这就是"负迁移"）。

Domain Adaptation（领域自适应）

一、什么是 Domain？

在机器学习中，一个 domain（领域） 可以理解为一个联合分布：

p(X,Y) p(X, Y) p(X,Y)

也就是说，一个任务的"世界"是由数据的分布决定的。

若 Y∈{1,2,...,C}Y \in \{1,2,\dots,C\}Y∈{1,2,...,C}，则是一个 分类问题（classification）；
若 Y∈RY \in \mathbb{R}Y∈R，则是一个 回归问题（regression）。

因此，不同的 domain 代表不同的数据来源和分布。比如，不同天气下的图像、不同地区的语言数据，都是不同的 domain。

二、源域与目标域

我们通常有两个分布：

源域（source domain） ：
ps(X,Y) p_s(X,Y) ps(X,Y)
目标域（target domain） ：
pt(X,Y) p_t(X,Y) pt(X,Y)

问题是：

在什么条件下，我们能直接使用源域上训练好的分类器去做目标域的预测？

答案是：只有当两者的分布非常接近时，模型才能泛化。如果分布不同，我们需要减少两个分布的差异。

三、核心思想：对齐分布差异

如果 ps(X,Y)p_s(X,Y)ps(X,Y) 与 pt(X,Y)p_t(X,Y)pt(X,Y) 差异较大（比如图像风格、背景光线、传感器不同），

那我们需要通过某种方法，使得源域与目标域在特征空间中的分布尽可能相似。

常见做法包括：

特征变换（Feature transformation）
对抗式对齐（Adversarial alignment）
核均值匹配（Kernel Mean Matching, KMM）

接下来我们重点讲 KMM，它是最早的经典方法之一。

四、Kernel Mean Matching（核均值匹配）

(1) 基本定义

我们用一个核函数（kernel function）来度量样本之间的相似度：

K(x1,x2)=⟨ϕ(x1),ϕ(x2)⟩ K(x_1,x_2) = \langle \phi(x_1), \phi(x_2) \rangle K(x1,x2)=⟨ϕ(x1),ϕ(x2)⟩

其中：

ϕ:X→H\phi: X \to \mathcal{H}ϕ:X→H 是将数据从原始空间映射到一个高维的 再生核希尔伯特空间 (RKHS)；
H\mathcal{H}H 是这个特征空间；
⟨⋅,⋅⟩\langle \cdot , \cdot \rangle⟨⋅,⋅⟩ 表示内积。

我们定义分布的核均值表示 为：
μ(p(X))=EX∼p(X)[ϕ(X)] \mu(p(X)) = \mathbb{E}_{X\sim p(X)}[\phi(X)] μ(p(X))=EX∼p(X)[ϕ(X)]

这意味着我们用特征映射的"平均"来代表整个分布。

如果核函数 KKK 是"通用核"，则 μ(p)\mu(p)μ(p) 可以唯一地刻画一个分布。

把每个样本 ϕ(X)\phi(X)ϕ(X) 看作一粒糖果，平均一下得到的"口味" μ(p(X))\mu(p(X))μ(p(X)) 就代表整袋糖的味道。

如果两袋糖的味道平均差不多，那这两袋糖（分布）就可以看作是一样的。

(2) 想法：让两域的"平均特征"一致

目标是让源域的加权特征均值与目标域的特征均值尽量接近：
μ(pt(X))=EX∼ps(X)[β(X)ϕ(X)] \mu(p_t(X)) = \mathbb{E}_{X\sim p_s(X)}[\beta(X)\phi(X)] μ(pt(X))=EX∼ps(X)[β(X)ϕ(X)]

其中 β(X)\beta(X)β(X) 是前面提到的权重因子 ，满足：
β(X)≥0,EX∼ps(X)[β(X)]=1. \beta(X) \ge 0,\quad \mathbb{E}_{X\sim p_s(X)}[\beta(X)] = 1. β(X)≥0,EX∼ps(X)[β(X)]=1.

直觉：我们在源域样本上调整权重 β(X)\beta(X)β(X)，让它们的"平均味道"匹配目标域。

当上式成立时：
μ(β(X)ps(X))=μ(pt(X)) \mu(\beta(X)p_s(X)) = \mu(p_t(X)) μ(β(X)ps(X))=μ(pt(X))

意味着两个分布在 RKHS 中的"均值嵌入"一致。

(3) 优化目标：学习权重 β(X)

我们希望最小化这两个均值表示之间的距离：
min⁡β∥μ(pt(X))−EX∼ps(X)[β(X)ϕ(X)]∥2 \min_{\beta} \left\| \mu(p_t(X)) - \mathbb{E}_{X\sim p_s(X)}[\beta(X)\phi(X)] \right\|^2 βmin μ(pt(X))−EX∼ps(X)[β(X)ϕ(X)] 2

同时满足约束：
β(X)≥0,EX∼ps(X)[β(X)]=1. \beta(X)\ge0,\quad \mathbb{E}_{X\sim p_s(X)}[\beta(X)]=1. β(X)≥0,EX∼ps(X)[β(X)]=1.

解释：

第一个约束防止出现负权；
第二个约束保证样本总权重不变；
目标函数则确保"分布的平均特征"在核空间中尽可能一致。

(4) 实际中如何求解？

我们通常只有样本，而没有真实分布。

假设：

源域样本：
{x1S,...,xnSS}∼ps(X) \{x_1^S,\ldots,x_{n_S}^S\} \sim p_s(X) {x1S,...,xnSS}∼ps(X)
目标域样本：
{x1T,...,xnTT}∼pt(X) \{x_1^T,\ldots,x_{n_T}^T\} \sim p_t(X) {x1T,...,xnTT}∼pt(X)

那么我们就可以用样本估计期望，把优化问题写成一个二次规划（QP）问题：

min⁡β∥1nT∑j=1nTϕ(xjT)−1nS∑i=1nSβiϕ(xiS)∥2 \min_{\beta} \left\| \frac{1}{n_T}\sum_{j=1}^{n_T}\phi(x_j^T) - \frac{1}{n_S}\sum_{i=1}^{n_S}\beta_i\phi(x_i^S) \right\|^2 βmin nT1j=1∑nTϕ(xjT)−nS1i=1∑nSβiϕ(xiS) 2

subject to
βi≥0,1nS∑i=1nSβi=1. \beta_i \ge 0, \quad \frac{1}{n_S}\sum_{i=1}^{n_S}\beta_i = 1. βi≥0,nS1i=1∑nSβi=1.

这就是 Kernel Mean Matching 的核心优化形式。

五、直觉总结

概念	数学表达	小学生能懂的类比
分布	p(X,Y)p(X,Y)p(X,Y)	两个世界的数据规律
目标	ps(X,Y)≈pt(X,Y)p_s(X,Y)\approx p_t(X,Y)ps(X,Y)≈pt(X,Y)	让两个世界"更像"
权重	β(X)=pt(X)ps(X)\beta(X)=\frac{p_t(X)}{p_s(X)}β(X)=ps(X)pt(X)	像目标世界的样本多加点分
核均值	μ(p(X))=E[ϕ(X)]\mu(p(X))=\mathbb{E}[\phi(X)]μ(p(X))=E[ϕ(X)]	整袋糖果的平均味道
对齐目标	μ(pt(X))≈μ(β(X)ps(X))\mu(p_t(X))\approx\mu(\beta(X)p_s(X))μ(pt(X))≈μ(β(X)ps(X))	调整源域糖果配比，让两袋糖味道一样

Two Transfer Learning Models（两种迁移学习模型）

一、回顾：目标与权重学习

在前面我们提到过目标风险：

RT(h)=E(X,Y)∼pt(X,Y)[ℓ(X,Y,h)] R^T(h) = \mathbb{E}_{(X,Y)\sim p_t(X,Y)}[\ell(X,Y,h)] RT(h)=E(X,Y)∼pt(X,Y)[ℓ(X,Y,h)]

由于目标域数据常常缺乏标签，我们用源域样本加权来近似它：

RT(h)≈1nS∑i=1nSβ(xiS,yiS)ℓ(xiS,yiS,h) R^T(h) \approx \frac{1}{n_S}\sum_{i=1}^{n_S}\beta(x_i^S, y_i^S)\ell(x_i^S, y_i^S,h) RT(h)≈nS1i=1∑nSβ(xiS,yiS)ℓ(xiS,yiS,h)

关键问题是：怎样学习出合适的权重 β(X,Y)\beta(X,Y)β(X,Y)？

二、概率的乘法法则（Product Rule of Probability）

首先，我们知道联合分布可以写成两种等价形式：

p(X,Y)=p(Y∣X)p(X)=p(X∣Y)p(Y) p(X,Y) = p(Y|X)p(X) = p(X|Y)p(Y) p(X,Y)=p(Y∣X)p(X)=p(X∣Y)p(Y)

这意味着 p(X,Y)p(X,Y)p(X,Y) 的变化可以从两方面理解：

协变量变化（Covariate shift） ：p(X)p(X)p(X) 变了；
标签变化（Target shift） ：p(Y)p(Y)p(Y) 变了。

于是我们得到两个模型思路。

三、模型一：Covariate Shift Model（协变量漂移模型）

(1) 基本假设

我们假设：
pt(Y∣X)=ps(Y∣X),pt(X)≠ps(X) p_t(Y|X) = p_s(Y|X), \quad p_t(X) \ne p_s(X) pt(Y∣X)=ps(Y∣X),pt(X)=ps(X)

也就是说，输入分布变了 ，但"给定 X 时 Y 的分布"没变。

换句话说，"规律"是一样的，只是"题目分布"不一样。

举例：训练数据来自晴天街景，测试数据来自阴天街景。路上标志规律没变，只是像素分布不同。

(2) 目标：学习 β(X)\beta(X)β(X)

由定义：
β(X,Y)=pt(X,Y)ps(X,Y) \beta(X,Y) = \frac{p_t(X,Y)}{p_s(X,Y)} β(X,Y)=ps(X,Y)pt(X,Y)

使用乘法法则展开：
β(X,Y)=pt(Y∣X)pt(X)ps(Y∣X)ps(X)=pt(X)ps(X)=β(X) \begin{aligned} \beta(X,Y) &= \frac{p_t(Y|X)p_t(X)}{p_s(Y|X)p_s(X)} \\ &= \frac{p_t(X)}{p_s(X)} = \beta(X) \end{aligned} β(X,Y)=ps(Y∣X)ps(X)pt(Y∣X)pt(X)=ps(X)pt(X)=β(X)

于是权重只与 XXX 有关。

这说明我们只需要匹配 pt(X)p_t(X)pt(X) 与 ps(X)p_s(X)ps(X) 。

例如使用 Kernel Mean Matching (KMM) 来估计 β(X)\beta(X)β(X)。

(3) 图形理解

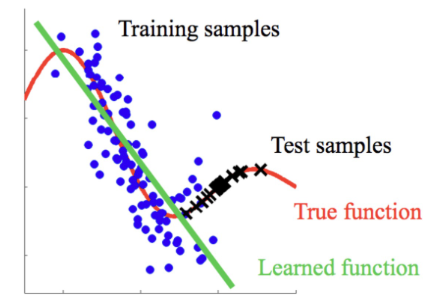
http://iwann.ugr.es/2011/pdf/InvitedTalk-FHerrera-IWANN11.pdf

蓝点：训练样本（源域）
黑叉：测试样本（目标域）
红线：真实函数（True function）
绿线：模型学习的函数（Learned function）

模型在源域表现很好，但测试分布不同，预测偏移。

通过加权修正（KMM），可以让模型重新对齐两域的分布。

四、模型二：Target Shift Model（目标漂移模型）

(1) 基本假设

我们假设：
pt(X∣Y)=ps(X∣Y),pt(Y)≠ps(Y) p_t(X|Y) = p_s(X|Y), \quad p_t(Y) \ne p_s(Y) pt(X∣Y)=ps(X∣Y),pt(Y)=ps(Y)

意思是：给定标签时，样本分布一样，但标签比例不同。

举个例子：

源域：0--9 手写数字各 10%；

目标域：数字"0""1"更多，数字"9"更少。
模型需要适应这种标签比例的变化。

(2) 推导权重 β(Y)\beta(Y)β(Y)

同样地：
β(X,Y)=pt(X,Y)ps(X,Y)=pt(X∣Y)pt(Y)ps(X∣Y)ps(Y)=pt(Y)ps(Y)=β(Y) \begin{aligned} \beta(X,Y) &= \frac{p_t(X,Y)}{p_s(X,Y)} \\ &= \frac{p_t(X|Y)p_t(Y)}{p_s(X|Y)p_s(Y)} \\ &= \frac{p_t(Y)}{p_s(Y)} = \beta(Y) \end{aligned} β(X,Y)=ps(X,Y)pt(X,Y)=ps(X∣Y)ps(Y)pt(X∣Y)pt(Y)=ps(Y)pt(Y)=β(Y)

因此在目标漂移中，权重只依赖于标签 YYY。

(3) 难点：目标域没标签怎么办？

如果目标域数据没有 YYY，那 β(Y)\beta(Y)β(Y) 怎么学？

我们可以利用核均值匹配思想，通过边缘分布对齐来估计。

(4) 基于分布匹配的学习过程

我们知道：
pt(Y)=β(Y)ps(Y) p_t(Y) = \beta(Y)p_s(Y) pt(Y)=β(Y)ps(Y)

将它代入联合分布的边缘化：
pt(X)=∫pt(X∣Y)pt(Y)dY=∫ps(X∣Y)β(Y)ps(Y)dY \begin{aligned} p_t(X) &= \int p_t(X|Y)p_t(Y)dY \\ &= \int p_s(X|Y)\beta(Y)p_s(Y)dY \end{aligned} pt(X)=∫pt(X∣Y)pt(Y)dY=∫ps(X∣Y)β(Y)ps(Y)dY

这意味着，只要让右边积分结果与目标域的 pt(X)p_t(X)pt(X) 相匹配，就能求得 β(Y)\beta(Y)β(Y)。

换句话说，我们让：
pt(X)≈∫ps(X∣Y)β(Y)ps(Y)dY p_t(X) \approx \int p_s(X|Y)\beta(Y)p_s(Y)dY pt(X)≈∫ps(X∣Y)β(Y)ps(Y)dY

(5) 优化目标

定义核均值表示后，得到优化形式：
min⁡β∥μ(pt(X))−EY∼ps(Y)[μ(ps(X∣Y))β(Y)]∥2 \min_{\beta} \left\| \mu(p_t(X)) - \mathbb{E}_{Y\sim p_s(Y)}\big[\mu(p_s(X|Y))\beta(Y)\big] \right\|^2 βmin μ(pt(X))−EY∼ps(Y)[μ(ps(X∣Y))β(Y)] 2

subject to:
β(Y)≥0,EY∼ps(Y)[β(Y)]=1. \beta(Y)\ge0,\quad \mathbb{E}_{Y\sim p_s(Y)}[\beta(Y)] = 1. β(Y)≥0,EY∼ps(Y)[β(Y)]=1.

经验估计版本为：
min⁡β∥1nT∑i=1nTϕ(xiT)−1nS∑i=1nSβ(yiS)μ^(ps(X∣yiS))∥2 \min_{\beta} \left\| \frac{1}{n_T}\sum_{i=1}^{n_T}\phi(x_i^T) - \frac{1}{n_S}\sum_{i=1}^{n_S}\beta(y_i^S)\hat{\mu}(p_s(X|y_i^S)) \right\|^2 βmin nT1i=1∑nTϕ(xiT)−nS1i=1∑nSβ(yiS)μ^(ps(X∣yiS)) 2

subject to:
β(yiS)≥0,1nS∑i=1nSβ(yiS)=1. \beta(y_i^S)\ge0,\quad \frac{1}{n_S}\sum_{i=1}^{n_S}\beta(y_i^S)=1. β(yiS)≥0,nS1i=1∑nSβ(yiS)=1.

直觉：

我们在不同类别的源域样本上分配不同的权重，让"生成的总体分布"与目标域的分布尽可能一致。

五、实际应用问题（Real-world problems）

在真实任务中，我们通常有：

源域：{(x1S,y1S),...,(xnSS,ynSS)}\{(x_1^S, y_1^S), \ldots, (x_{n_S}^S, y_{n_S}^S)\}{(x1S,y1S),...,(xnSS,ynSS)}
目标域：{x1T,...,xnTT}\{x_1^T, \ldots, x_{n_T}^T\}{x1T,...,xnTT}（标签缺失）

问题是：

我们该用哪个模型？Covariate shift 还是 Target shift？

答案：视实际场景而定。

若输入分布不同而规律相同，用 Covariate shift model；
若标签分布不同而类别特征相似，用 Target shift model。

六、延伸：研究主题（State-of-the-art Methods）

当前研究前沿集中在：

同时考虑 p(X)p(X)p(X) 与 p(Y)p(Y)p(Y) 都变化的情形；
结合深度学习的对抗式域对齐（Adversarial Domain Adaptation）；
基于最优传输（Optimal Transport）的分布匹配；
多源域与多任务迁移（Multi-source / Multi-task Transfer）。

一句话总结：

Covariate Shift：世界的规则不变，只是输入环境换了；

Target Shift：世界的样本规律不变，只是各类比例变了；

两者都是在寻找"如何加权"，让源域知识更好地服务目标域。