深度学习：动量梯度下降实战（Momentum Gradient Descent）

关键词解释：动量梯度下降（Momentum Gradient Descent）

💡 动量法通过引入"惯性"机制，显著提升梯度下降的收敛速度与稳定性。

✅ 一、为什么需要动量？

标准梯度下降在遇到以下情况时表现不佳：

损失函数存在狭窄山谷 → 参数更新左右震荡；
梯度噪声大 → 路径杂乱；
局部极小值/鞍点 → 容易卡住。

动量法的核心思想：

让参数更新不仅依赖当前梯度，还继承历史梯度的方向，就像一辆有质量的车------转弯更稳，下坡更快。

✅ 二、数学原理

动量梯度下降使用指数加权平均来平滑梯度：

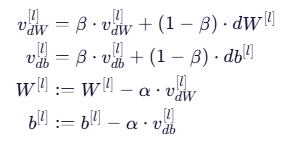
其中：

：动量系数（通常取 0.9）；
：学习率；
：速度（velocity），即梯度的历史加权平均。

📌 注：此处未使用偏差修正（bias correction），这是经典 Momentum 的常见做法。若需修正，可在初期除以。

✅ 三、代码实现详解

3.1 初始化速度字典

复制代码

def initialize_velocity(parameters):
    L = len(parameters) // 2  # 网络层数
    v = {}
    for l in range(L):
        v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])
    return v

✅ 作用：为每一层的权重和偏置初始化速度为零向量。

3.2 动量参数更新

复制代码

def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
    L = len(parameters) // 2

    for l in range(L):
        # 更新速度（指数加权平均）
        v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads["dW" + str(l + 1)]
        v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads["db" + str(l + 1)]

        # 使用速度更新参数
        parameters["W" + str(l + 1)] -= learning_rate * v["dW" + str(l + 1)]
        parameters["b" + str(l + 1)] -= learning_rate * v["db" + str(l + 1)]

    return parameters, v

✅ 关键点：

先更新速度 v；

再用 v 更新参数；

W 对应 dW，b 对应 db ------ 一一对应，不可混淆。

✅ 四、测试与验证

复制代码

parameters, grads, v = update_parameters_with_momentum_test_case()
parameters, v = update_parameters_with_momentum(
    parameters, grads, v, beta=0.9, learning_rate=0.01
)

print("W1 =", parameters["W1"])
print("b1 =", parameters["b1"])
print("W2 =", parameters["W2"])
print("b2 =", parameters["b2"])
print("v['dW1'] =", v["dW1"])
print("v['db1'] =", v["db1"])
print("v['dW2'] =", v["dW2"])
print("v['db2'] =", v["db2"])

✅ 预期行为：

W1 是矩阵（如 (2, 2)）；
b1 是向量（如 (1, 2)）；
v["dW1"] 与 grads["dW1"] 同维；
所有值均为合理浮点数，无 nan 或异常。

✅ 五、超参数建议

超参数	推荐值	说明
β（beta）	0.9	表示保留 90% 的历史梯度方向
学习率 α	0.001 ~ 0.01	可配合学习率衰减使用
是否用偏差修正	否（经典 Momentum）	Adam 才常用修正

💡 经验法则 ：

若训练初期 loss 下降缓慢，可尝试增大 β（如 0.95）；

若震荡严重，可减小 β（如 0.8）。

✅ 六、动量 vs 标准 GD 对比

特性	标准梯度下降	动量梯度下降
收敛速度	慢	快
路径稳定性	震荡大	平滑
抗噪声能力	弱	强
实现复杂度	简单	略高（需维护 v）

🌟 适用场景 ：

几乎所有现代深度学习任务都推荐使用动量或其变体（如 Adam）。

✅ 七、总结

动量梯度下降 = 历史智慧 + 当前信息

它让优化过程不再"盲目跳跃"，而是"带着记忆前行"。