一小时速通Pytorch之神经网络相关知识（三）

钅日 勿 XiName2025-11-16 13:50

Neural Networks神经网络

  • 通过官网学习总结而得，加上一些个人的理解。
  • Neural Networks在torch中简称nn，中文神经网络。
  • 文章中的图片（除了特别声明以外），均出自官网

概述

  • 在pytorch中通过torch.nn可以很方便的去构建一个神经网络。

  • 现在我们已经对autograd有了一定的认识。nn模块依赖于autograd机制去定义和区分模型。

  • 一个nn.Module（神经网络模型）包含很多层和一个前向传播的方法以及输出的值。

例如在一个经典的数字识别模型中，由一个输入层(INPUT)，多个中间的隐藏层，如卷积层(Convolutions)，下采样操作(Subsampling)，全连接层(Full connection)和输出层(OUTPUT)等，下面是一个经典的数字识别模型示意图：

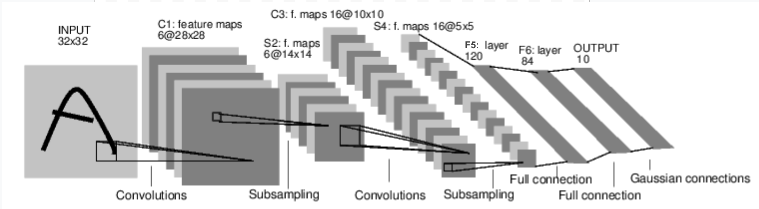
从图中可以看出，这是一个前馈神经网络。它接受输入，然后把输入的图像一层层传递到最后一层，最后输出结果。

在一个神经网络的常规训练有以下几个步骤：

  • 在神经网络中定义一些可以用来学习的参数（权重）
  • 多次迭代输入的数据集
  • 通过神经网络处理输入的信息
  • 计算损失值（这一次输出的结果与真实值直接的距离）
  • 把损失值的梯度信息反向传播给神经网络中的参数
  • 更新神经网络的权重参数。一般的权重更新公式如下：weight = weight -learning_rate * gradient（新权重 = 旧权重 - 学习率 * 梯度）

定义和使用神经网络

在传统的神经网络概念中，卷积层 ，线性层 ，全连接层 ，池化层 ，激活层 都是平等的概念，都是神经网络中的一层 。但是在pytorch中，为了优化性能和节省内存空间，只把卷积层 ，线性层 等这些需要存储参数的层 （需要学习权重信息的层）注册到nn.Model里面，由pytorch自动维护。形如**relu激活层，池化层 ，展平层 这些没有需要学习的参数，只是对输入做一个纯数学变化（例如relu激活层就是对输入做一个relu函数），这类的 层都统一放在 forward函数**里面。

下面定义一个神经网络，示例：

python 复制代码 
import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 第一层卷积层
        # 输入 1 张单通道的图像，输出 6 通道的值，采用 5*5 的卷积核
        self.conv1 = nn.Conv2d(1, 6, 5)
        # 第二层卷积层
        # 输入 6 通道的值，输出 16 通道的值，采用 5*5 的卷积核
        self.conv2 = nn.Conv2d(6, 16, 5)
        # 第一层线性层，对输入 X 得到 Y = WX + B，执行线性变化操作
        # 第二层的卷积层的输出是 16 * 5 *  5作为这一层的输入
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        # 第二层线性层
        self.fc2 = nn.Linear(120, 84)
        # 第三层线性层
        self.fc3 = nn.Linear(84, 10)

    def forward(self, input):
        # 卷积层 C1：1 个输入图像通道，6 个输出通道，
        # 5x5 平方卷积，它使用 RELU 激活函数，并且
        # 输出一个大小为 （N， 6， 28， 28） 的 张量，其中 N 是批次的大小
        c1 = F.relu(self.conv1(input))
        # 下采样采样层 S2：2x2 网格，纯函数式，
        # 该层没有任何参数，输出一个（N，6,14,14）张量
        s2 = F.max_pool2d(c1, (2, 2))
        # 卷积层 C3：6 个输入通道，16 个输出通道，
        # 5x5 平方卷积，它使用 RELU 激活函数，并且
        # 输出一个 （N， 16， 10， 10） 张量
        c3 = F.relu(self.conv2(s2))
        # 下采样层 S4：2x2 网格，纯函数式，
        # 该层没有任何参数，输出一个（N，16,5,5）张量
        s4 = F.max_pool2d(c3, 2)
        # 展平层：纯函数式，输出一个 （N， 400） 张量
        s4 = torch.flatten(s4, 1)
        # 全连接层 F5：输入一个 （N， 400） 张量 ，
        # 并输出一个 （N， 120） 张量，它使用 RELU 激活函数
        f5 = F.relu(self.fc1(s4))
        # 全连通层F6：（N，120）张量 输入，
        # 并输出一个 （N， 84） 张量，它使用 RELU 激活函数
        f6 = F.relu(self.fc2(f5))
        # 高斯层 OUTPUT：输入一个 （N， 84） 张量，以及
        # 输出一个 （N， 10） 张量
        output = self.fc3(f6)
        return output


net = Net()
print(net)

示例输出：

复制代码 
Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

在这里我们只定义模型的基本结构和前向传播函数（forward），反向传播会使用我们输入的梯度信息自动计算梯度和自动进行反向传播。并且我们可以在前向传播的函数里面随意使用张量的操作。

我们可以通过调用net.parameters()来获取神经网络里面的可以学习参数。

例如：

python 复制代码 
params = list(net.parameters())
print(len(params))
print(params[0].size())  # 第一个卷积层的参数形状

示例输出：

复制代码 
10
torch.Size([6, 1, 5, 5])

接下来让我们尝试一个随机的32x32的灰度图像的输入。注意：此网络（LeNet）的预期输入大小为32 * 32 * 1。如果要在MNIST数据集上使用此网络，请将数据集中的图像大小调整为32 * 32 * 1

例如：

python 复制代码 
input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

示例输出：

复制代码 
tensor([[-0.0454, -0.1774,  0.0771,  0.1430,  0.0339,  0.1707,  0.0106,  0.0685,
         -0.0661, -0.0106]], grad_fn=<AddmmBackward0>)

这里输出一组十维的张量，其中值最大的即为预测的类别。（但是这里还没有学习，输入的也不是真正的数字）

接着，将所有参数的梯度缓冲区归零，并使用随机梯度进行反向传播：（实际情况我们需要传入损失值的梯度信息）

示例：

python 复制代码 
net.zero_grad()
out.backward(torch.randn(1, 10))

注意事项

torch.nn仅支持小批次（一次训练中传入照片的数量，理解为几张照片一起学习）训练，而且整个torch.nn包仅支持小批量样本的输入，而不支持单个样本。

例如，nn.Conv2d将接受n个样本 * n个通道 * 高度 * 宽度的4D张量。

如果你只有单个的样本，使用input.unsqueeze(0)来添加一个虚拟的批次维度。

在继续下一步的操作之前，来进行一个简单的知识回顾：

  • torch.Tensor，一个可以支持反向传播，autograd机制的多维数组，同时也会保留张量的梯度信息。
  • nn.model神经网络模型。提供了封装参数的便捷方式，有助于将参数移动到GPU、导出、加载等。
  • nn.Parameter一种特殊的张量。当作为属性分配给模型时，会自动注册为参数。
  • autograd.Function实现自动梯度操作的前向传播和反向传播。每个Tensor操作至少创建一个Function节点，该节点连接到创建Tensor的函数并对其历史进行编码。

在本节中，我们学习了：

  • 定义一个神经网络模型
  • 前向传播输入的数据并且调用了一次反向传播

接下来我们继续学习：

  • 计算损失值
  • 更新神经网络的参数

损失函数

损失函数接受一对**（输出值，目标值）的数据，然后计算 输出值与真实值**之间的距离。

在nn这个包下定义一些常用的损失函数。例如均方误差损失 函数可以通过nn.MSELoss来调用

示例：

python 复制代码 
# 损失函数
output = net(input)
target = torch.randn(10)  # 示例一组标签值
target = target.view(1, -1)  # 给 target 变一下形状与 output匹配上，这里的 target 本身也是一组十维的数据，不知道作者有何用意？？？
criterion = nn.MSELoss()

loss = criterion(output, target)
print("损失值{}".format(loss))
print(loss)

示例输出：

复制代码 
损失值1.3122848272323608
tensor(1.3123, grad_fn=<MseLossBackward0>)

现在，如果你使用loss的.grad_fn属性反向跟踪loss，你会看到一个计算图，如下所示：

复制代码 
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> flatten -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

因此，当我们调用loss.backward（）时，整个计算图相对于神经网络参数是微分的，计算图中所有requires_grad=True的张量都会将其.grad张量与梯度一起累加。

为了更好说明，让我们把损失值反向传播几步：

python 复制代码 
print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

示例输出：

复制代码 
<MseLossBackward0 object at 0x000002132063A950>
<AddmmBackward0 object at 0x000002132063A8F0>
<AccumulateGrad object at 0x000002132063A8F0>

误差反向传播算法(Backprop)

我们通过调用loss.backward()把误差进行反向传播到神经网络的每一个神经元当中。需要注意的是，我们每一次都需要清除已经存在的梯度信息，否组本次的梯度信息会受到之前信息的影响。

现在，我们正式调用loss.,backward()，并且关注第一层卷积层的偏差值在进行反向传播前后的变化。

示例：

python 复制代码 
net.zero_grad()  # 将所有参数的梯度缓冲区清零
print('第一层卷积层在进行反向传播前的偏差值为：{}'.format(net.conv1.bias.grad))
loss.backward()
print('第一层卷积层在进行反向传播后的偏差值为：{}'.format(net.conv1.bias.grad))

示例输出：

复制代码 
第一层卷积层在进行反向传播前的偏差值为：None
第一层卷积层在进行反向传播后的偏差值为：tensor([ 0.0114, -0.0034, -0.0002,  0.0101,  0.0018,  0.0072])

可以看到我们确实把损失值的梯度传到了第一层的卷积层，损失函数的使用到此结束，下面我们将结束如何利用这些梯度信息更新我们的权重参数

更新权重

在一般的训练过程中，我们都是采用**随机梯度下降（SGD）**的方法进行更新权重，随机梯度下降的一般公式为：

复制代码 
weight = weight - learning_rate * gradient
新权重 = 旧权重 - 学习率 * 梯度值

我们可以采几行的python代码来实现SGD

示例：

python 复制代码 
learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

这里注意，张量带_后缀的方法都是原地修改值

当然了，我们在实际的训练中不可能只使用SGD 进行更新参数，还可以使用Nesterov-SGD, Adam, RMSProp等更新方法。为了使更新权重值更加的方便，torch.optim已经封装好了上述的优化方法。

示例：

python 复制代码 
from torch import optim

# 创建一个优化器
optimizer = optim.SGD(net.parameters(), lr=0.01)

# 在训练过程中迭代下面的操作
optimizer.zero_grad()# 清空已有的梯度信息
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()  # 采用我们的优化器对参数进行更新

根据实际情况设计批次大小和迭代次数。

注意事项

每次迭代都必须清空梯度信息，否则一直累加的梯度会得到一个意外的结果。

完整代码

python 复制代码 
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim
from torch import optim


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 第一层卷积层
        # 输入 1 张单通道的图像，输出 6 通道的值，采用 5*5 的卷积核
        self.conv1 = nn.Conv2d(1, 6, 5)
        # 第二层卷积层
        # 输入 6 通道的值，输出 16 通道的值，采用 5*5 的卷积核
        self.conv2 = nn.Conv2d(6, 16, 5)
        # 第一层线性层，对输入 X 得到 Y = WX + B，执行线性变化操作
        # 第二层的卷积层的输出是 16 * 5 *  5作为这一层的输入
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        # 第二层线性层
        self.fc2 = nn.Linear(120, 84)
        # 第三层线性层
        self.fc3 = nn.Linear(84, 10)

    def forward(self, input):
        # 卷积层 C1：1 个输入图像通道，6 个输出通道，
        # 5x5 平方卷积，它使用 RELU 激活函数，并且
        # 输出一个大小为 （N， 6， 28， 28） 的 张量，其中 N 是批次的大小
        c1 = F.relu(self.conv1(input))
        # 下采样采样层 S2：2x2 网格，纯函数式，
        # 该层没有任何参数，输出一个（N，6,14,14）张量
        s2 = F.max_pool2d(c1, (2, 2))
        # 卷积层 C3：6 个输入通道，16 个输出通道，
        # 5x5 平方卷积，它使用 RELU 激活函数，并且
        # 输出一个 （N， 16， 10， 10） 张量
        c3 = F.relu(self.conv2(s2))
        # 下采样层 S4：2x2 网格，纯函数式，
        # 该层没有任何参数，输出一个（N，16,5,5）张量
        s4 = F.max_pool2d(c3, 2)
        # 展平层：纯函数式，输出一个 （N， 400） 张量
        s4 = torch.flatten(s4, 1)
        # 全连接层 F5：输入一个 （N， 400） 张量 ，
        # 并输出一个 （N， 120） 张量，它使用 RELU 激活函数
        f5 = F.relu(self.fc1(s4))
        # 全连通层F6：（N，120）张量 输入，
        # 并输出一个 （N， 84） 张量，它使用 RELU 激活函数
        f6 = F.relu(self.fc2(f5))
        # 高斯层 OUTPUT：输入一个 （N， 84） 张量，以及
        # 输出一个 （N， 10） 张量
        output = self.fc3(f6)
        return output


net = Net()
print(net)

params = list(net.parameters())
print(len(params))
print(params[0].size())  # 第一个卷积层的参数形状

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

net.zero_grad()
out.backward(torch.randn(1, 10))

# 损失函数
output = net(input)
target = torch.randn(10)  # 示例一组标签值
target = target.view(1, -1)  # 给 target 变一下形状与 output匹配上，这里的 target 本身也是一组十维的数据，不知道作者有何用意？？？
criterion = nn.MSELoss()

loss = criterion(output, target)
print("损失值{}".format(loss))
print(loss)

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

# net.zero_grad()  # 将所有参数的梯度缓冲区清零
# print('第一层卷积层在进行反向传播前的偏差值为：{}'.format(net.conv1.bias.grad))
# loss.backward()
# print('第一层卷积层在进行反向传播后的偏差值为：{}'.format(net.conv1.bias.grad))
#
# learning_rate = 0.01
# for f in net.parameters():
#     f.data.sub_(f.grad.data * learning_rate)

# 创建一个优化器
optimizer = optim.SGD(net.parameters(), lr=0.01)

# 在训练过程中迭代下面的操作
optimizer.zero_grad()
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()  # 采用我们的优化器对参数进行更新
相关推荐
你也渴望鸡哥的力量么3 小时前
GeoSeg 框架解析
人工智能
唐华班竹3 小时前
PoA 如何把 CodexField 从“创作平台”推向“内容经济网络”
人工智能·web3
渡我白衣3 小时前
深入理解 OverlayFS：用分层的方式重新组织 Linux 文件系统
android·java·linux·运维·服务器·开发语言·人工智能
IT_陈寒3 小时前
Vue 3.4 正式发布：5个不可错过的性能优化与Composition API新特性
前端·人工智能·后端
极客BIM工作室3 小时前
解密VQVAE中的Codebook
人工智能
DogDaoDao4 小时前
大语言模型四大核心技术架构深度解析
人工智能·语言模型·架构·大模型·transformer·循环神经网络·对抗网络
shayudiandian4 小时前
Transformer结构完全解读：从Attention到LLM
人工智能·深度学习·transformer
天天爱吃肉82184 小时前
新能源汽车动力系统在环（HIL）半实物仿真测试台架深度解析
人工智能·python·嵌入式硬件·汽车
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05Linux下V2Ray安装配置指南06jdk21下载、安装（Windows、Linux、macOS）07综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件08使用国内镜像网站在线下载安装Qt（解决官网慢的问题）——Qt09《大数据技术原理与应用》实验报告三 熟悉HBase常用操作10智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践