一、基本概念
对于一些数据范围很大但是实际有效数据却很少的情况我们可以使用离散化对有效数据进行重新映射,从而达到缩小数据范围,减少时间复杂度的能力。
例如:一道题目中需要从1~1e9的范围内随机选择100个数据进行后面的操作(这个操作会是各种各样的)。很显然,我们创建一个1e9+10大小的数组记录那100给数据很不划算,这样我们就能够使用离散化------其实就是个那些数重新小到大排序并使用1~100(暂时不考虑重复)的数字来代替原本的数据。
离散化模板
模板1:
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
ll pos=0; ll n;
//原数组
ll a[N];
//离散化数组
ll dis[N];
ll find(ll x)
{
ll left = 1, right = pos;
while (left < right)
{
ll mid = left + (right - left+1) / 2;
if (dis[mid] > x)
{
right = mid - 1;
}
else
{
left = mid;
}
}
return left;
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> a[i];
dis[++pos] = a[i];
}
sort(dis+1, dis + pos+1);
pos = unique(dis+1, dis + pos+1) - (dis+1);
for (int i = 0; i <n; i++)
{
cout << a[i] << "离散化后:" << find(a[i]) << endl;
}
return 0;
}对于模板1其实就是除了创建一个原数组以外还创建一个离散化(dis)数组用来记录原数组元素离散化后映射的值,模板的情景并不复杂,其离散化数组记录的是原数组经过sort排序及nuique去重处理后的元素下标。
find函数则是使用二分查找的方式检索目标值的离散后的映射值。
模板2:
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
typedef long long ll;
ll pos = 0; ll n;
const int N = 1e5 + 10;
ll a[N];
unordered_map<ll, ll>dis;
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
sort(a, a + n);
for (int i = 0; i < n; i++)
{
if (dis.count(a[i])==0)
{
dis[a[i]] = ++pos;
}
}
for (int i = 0; i < n; i++)
{
cout << a[i] << "离散化后:" << dis[a[i]] << endl;
}
return 0;
}模板2的离散化目的都是一样的,只不过在具体形式上使用unordered_map哈希表来记录原数组离散化后的映射值,sort排序以及去重工作一样不能少。
小总结:
1、离散化的目的是降低检索范围--也就是适用于数据范围很大但实际数据不多的场景
2、离散化有两个核心步骤:排序(保留相对关系,确保映射 "有逻辑意义" )和去重(避免索引浪费,保证 "一个数据一个位置")
3、离散后的映射值有专门的结构进行存储
例题1:火烧赤壁

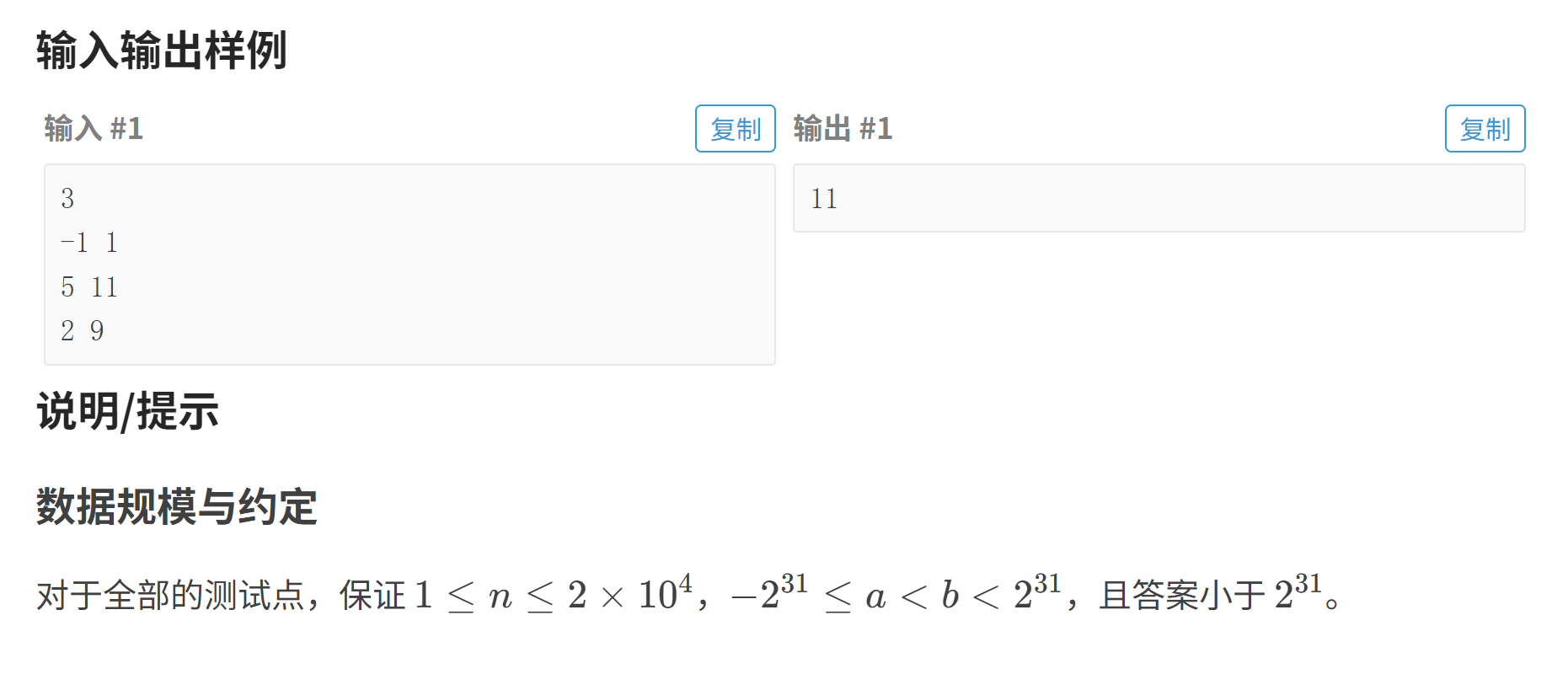
先看数据范围:n明显小于a,b,这时候就可以使用离散化减少检索范围。
再看看题目,我们发现需要求的是一排船中着火的船数,并且着火的范围是通过区间来提供的。这时候就要想到前缀和------着火起点自增1,着火末尾点自减1(题目中说明了是左闭右开)。再通过前缀和还原原数组(着火情况),若数组元素大于0就表示该点着火。
前缀和这里不是重点,重点来看看离散化是怎么实现的。
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
typedef long long ll;
const int N = 2e4 + 10;
ll a[N] = {0}, b[N] = { 0 };
ll dis[2*N];
unordered_map<ll, ll>id;
ll pos = 0;
ll f[2 * N];
int main()
{
int n; cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i] >> b[i];
dis[++pos] = a[i];
dis[++pos] = b[i];
}
sort(dis + 1, dis + 1 + pos);
pos = unique(dis + 1, dis + 1 + pos) - (dis + 1);
for (int i = 1; i <= pos; i++)
{
id[dis[i]] = i;
}
for (int i = 1; i <=n; i++)
{
ll left = id[a[i]]; ll right = id[b[i]];
f[left]++; f[right]--;
}
for (int i = 1; i <= pos; i++)
{
f[i] += f[i - 1];
}
ll le = 0, ri = 0; ll sum = 0;
for (int i = 1; i <= pos; i++)
{
if (f[i] > 0)
{
le = dis[i];
int j = i;
while (j <= pos && f[j] > 0)
{
j++;
}
ri = dis[j];
sum = sum + (ri - le);
i = j;
}
}
cout << sum;
return 0;
}很明显,要想使用前缀和还原就必须具备区分"着火点"和"着火末尾点"这两组数据。我们就干脆分别使用a,b两个数组分别表示记录。
尽管将两者分开,但还是需要一个数组dis来记录所有的元素,再通过对dis数组排序、去重后就能进行离散化处理。
我们使用unordered_map哈希表类型存储离散后的映射值,由于已经经过了去重,就可以进行插入操作------原数据为键,映射值为链,原数据保存在dis数组中
for (int i = 1; i <= pos; i++)
{
id[dis[i]] = i;
}离散化之后就是前缀和还原操作,f为还原数组,f数组以映射值为主(下标作为映射值,数组元素用于还原)。由于离散化数组id记录了映射关系,就可以直接依次获取a,b数组中组合元素的映射关系:
for (int i = 1; i <=n; i++)
{
ll left = id[a[i]]; ll right = id[b[i]];
f[left]++; f[right]--;
}此后的还原等处理就很简单了,但还是要注意:最终借助f数组计算着火长度时一定要使用原数组元素!!
le = dis[i];
ri = dis[j];样例2:贴海报

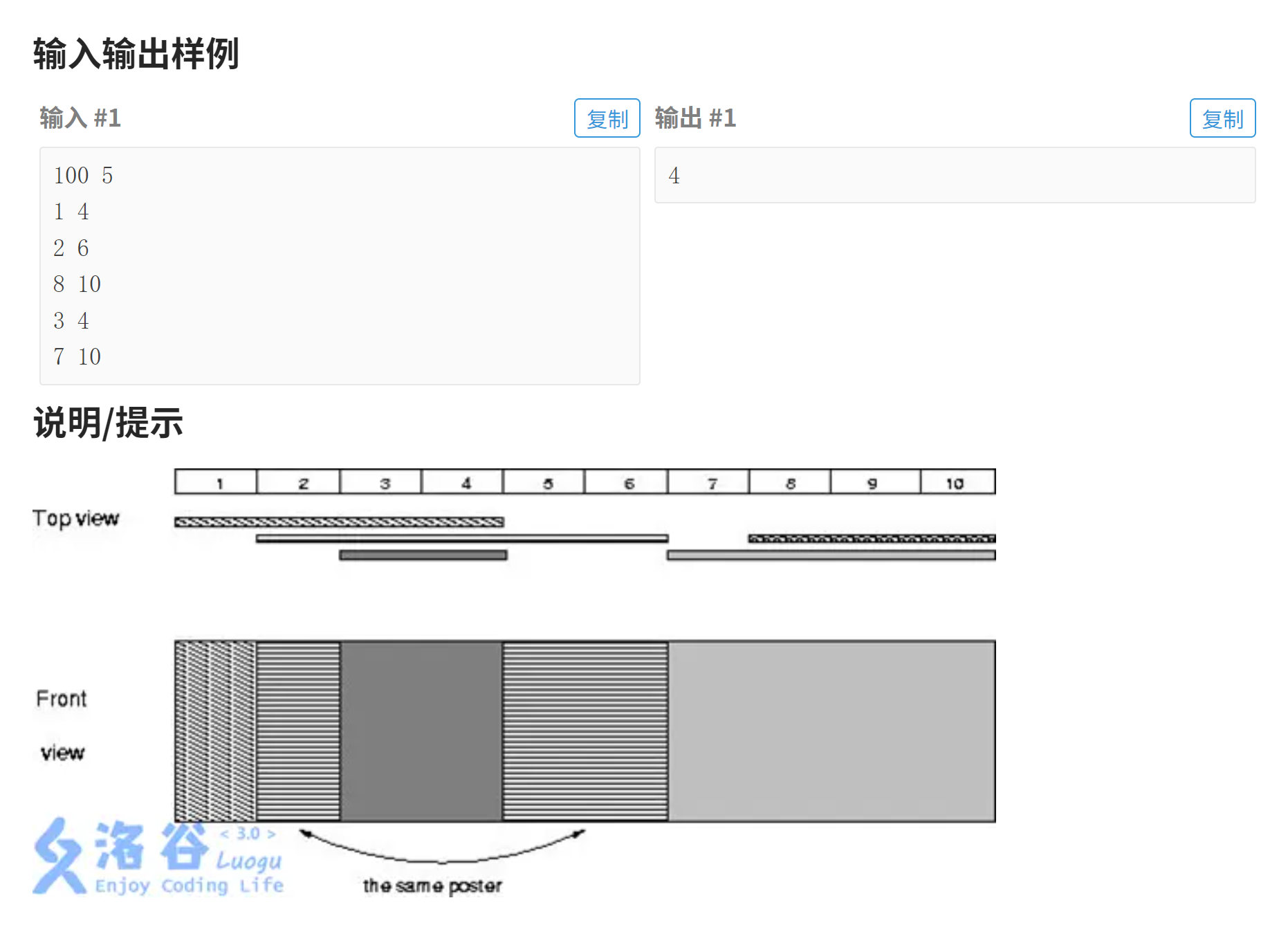

看到这个数据范围时我们同样可以往离散化上去想。
这道题的解法可以是离散化+模拟,模拟就是按照输入的数据对数组中的元素进行覆盖处理,最终能够看到多少海报就取决于数组中能看到多少个不同的数字(要排除给数组初始化的数值,我这里是0),离散化的思路上大体是一样的,就是在细节上会有需要注意的地方。
因为这道题不像是上一道题那样是通过左右区间位置之差来计算区间元素个数,而是需要遍历数组来观察元素值的。
这就不得不考虑到离散化的弊端--会将操作区间缩短,这可能会导致关键数据被覆盖!!
例如 [2, 5], [2, 3], [5, 6],离散化后: [1, 3], [1, 2], [3, 4]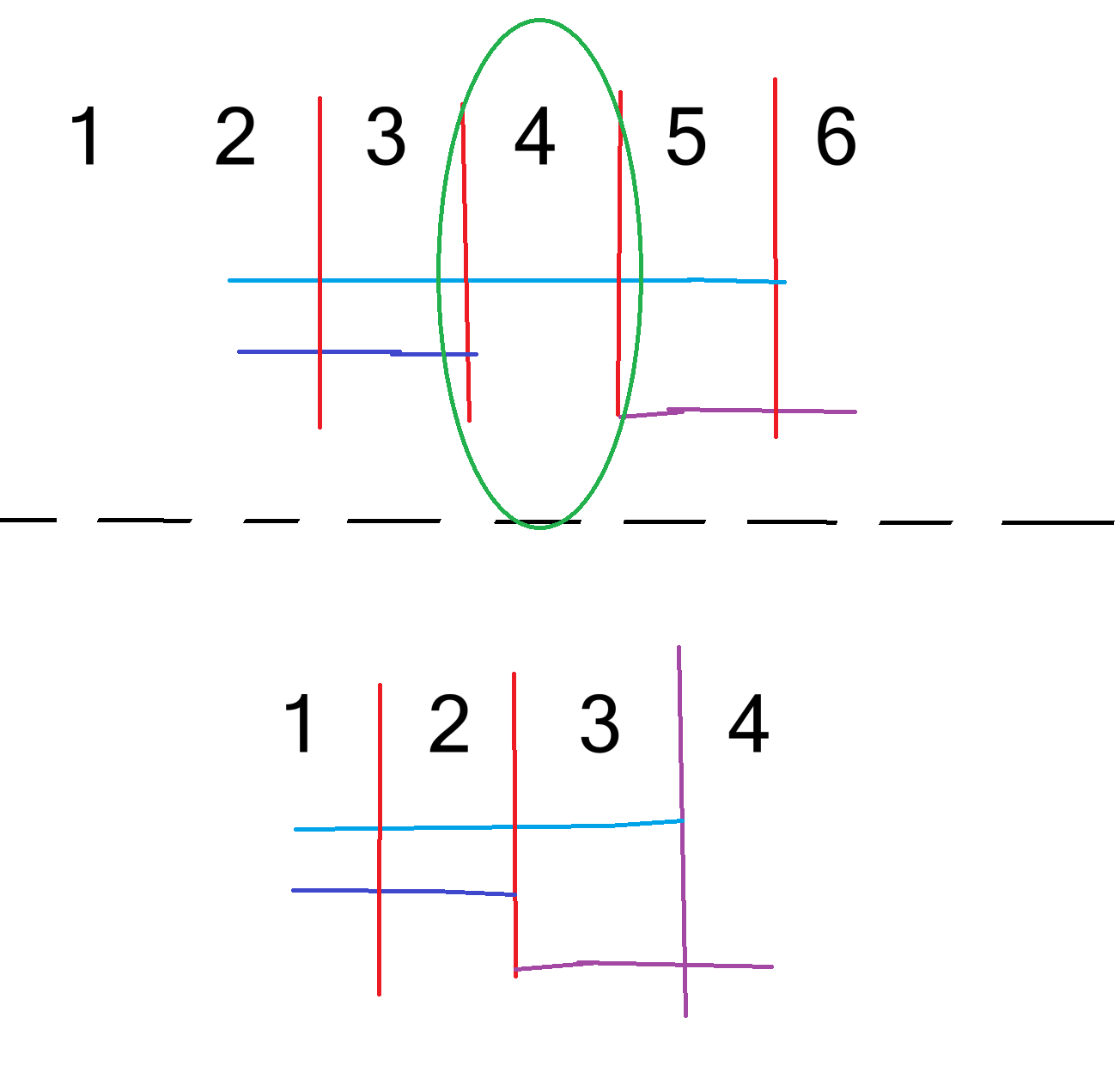
为了解决这个问题,我们在离散化区间 [x,y] 时把 [x+1,y+1] 也离散化进去,这样区间与区间之间就会产生空隙从而避免该问题。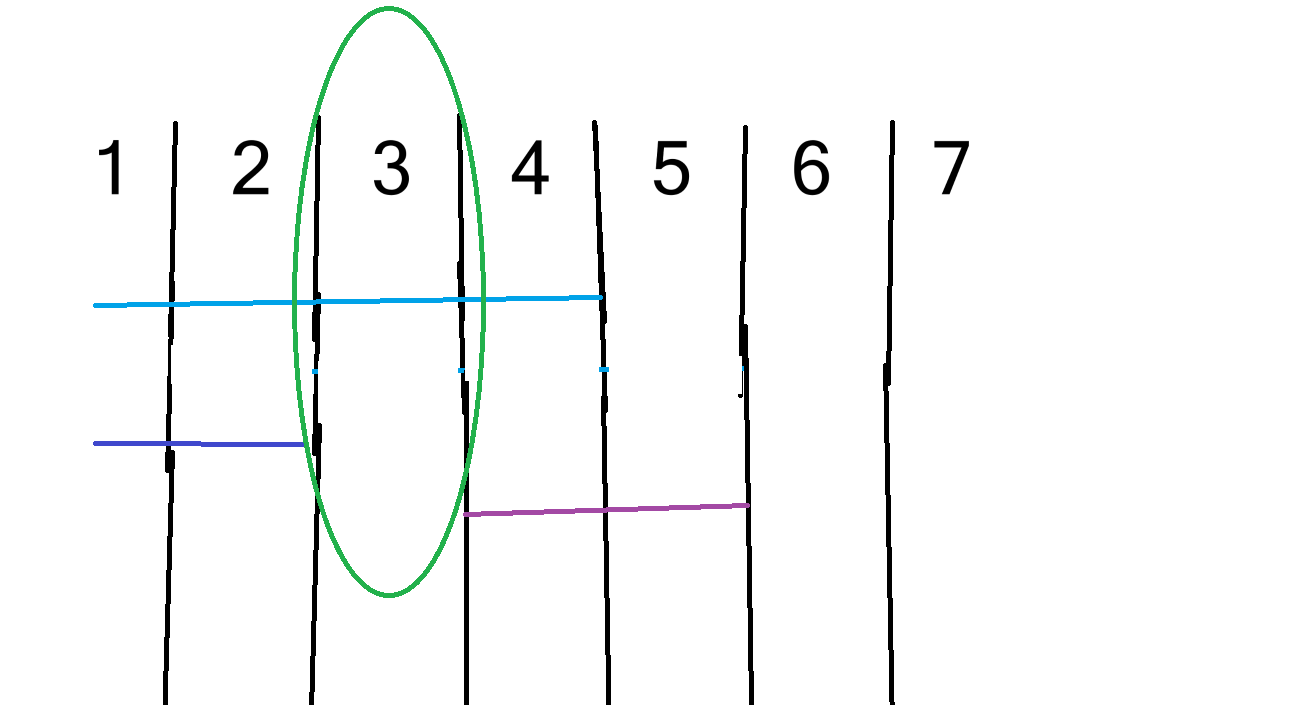
从图中就可以看出来,这其实就是给各区间之间留了一个单位的空隙间隔,防止了区间之间的互相粘黏。
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
typedef long long ll;
const int N = 1e3 + 10;
ll n, m;
ll a[N] = { 0 }, b[N] = { 0 };
ll dis[4 * N] = { 0 }; ll pos = 0;
unordered_map<ll, ll> id;
ll f[4 * N] = { 0 };
//插一嘴,bool类型数组初始化最好还是以false为准
bool ex[4 * N] = {false};
//离散化+模拟
int main()
{
cin >> n>> m;
for (int i = 1; i <= m; i++)
{
cin >> a[i] >> b[i];
dis[++pos] = a[i]; dis[++pos] = a[i] + 1;
dis[++pos] = b[i]; dis[++pos] = b[i] + 1;
}
//离散化
sort(dis + 1, dis + 1 + pos);
ll cnt = 0;
for (int i = 1; i <= pos; i++)
{
if (id.count(dis[i]) == 0)
{
id[dis[i]] = ++cnt;
}
}
for (int i = 1; i <=m ; i++)
{
ll le = id[a[i]]; ll ri = id[b[i]];
for (ll x = le; x <= ri; x++)
{
f[x] = i;
}
}
ll sum = 0;
for (int i = 1; i <=cnt; i++)
{
if (f[i] != 0 && !ex[f[i]])
{
sum++;
ex[f[i]] = true;
}
}
cout << sum;
return 0;
}总结
1、离散化解决的是数据范围太大而数据个数不多的情况,其通过类似哈希的映射方式缩小检索范围减少时间复杂度
2、离散化作为一种思想,常常会跟其它算法结合使用,在这个情况下离散化就有点象个"辅助",离散化的具体实现方式很大程度上受到其合作的算法影响。
3、离散化需要进行排序(方便用下标作为映射值)和去重(避免索引浪费,保证 "一个数据一个位置")
4、离散化有个缺点--在对区间进行离散化的时候很容易照成区间缩小的错误,这时候就需要将 [x+1,y+1] 也同时参与离散化但是不参与最后的原始数据参与的计算中(就是个占位置的家伙),以此减少区间的粘连性。