注:本文为"数学学习 | 本科数学荐书"相关讨论及文中提到的笔记合辑。
略作重排,如有内容异常,请看原文。
本科阶段值得推荐的优质数学书籍分享
一、工业界视角下的数学书籍组合(CodeCrafter 分享)
CodeCrafter 编辑于 2023-02-19 08:51
在工业界深耕算法领域十余年,从早期推荐系统、广告 CTR 预估到如今的大模型应用,数学始终是关键工具。探讨"最好的数学书",本质是寻找能传递数学思维并赋能实际问题解决的著作。对工业界从业者而言,不存在单一"最好"的数学书,更有效的是覆盖关键领域的"知识组合"。
1. 线性代数基础:Gilbert Strang《Introduction to Linear Algebra》
该书价值在于跳出计算层面,传递线性代数的本质逻辑。作者强调矩阵的四个基本子空间及相互关系,引导读者从几何与空间视角理解向量、矩阵及变换------将矩阵视为空间变换,将线性方程组求解理解为"寻找经特定变换可达目标点的向量"。

在实际应用中,例如推荐系统的 SVD 奇异值分解,书中以"任何矩阵均可表示为'旋转 - 拉伸 - 再旋转'的组合"( U U U 和 V V V 为旋转操作, Σ \Sigma Σ 为拉伸操作)的通俗解释,揭示了降维和特征提取的底层逻辑,帮助理解 SVD 用于协同过滤与缺失值填补的原理,这种直观认知远胜于单纯记忆公式。
2. 概率统计应用:Larry Wasserman《All of Statistics》
作为数据科学的重要基础,概率论与统计的学习需兼顾理论与实用。该书副标题为"A Concise Course in Statistical Inference",聚焦统计推断的重要思想,衔接机器学习应用场景,涵盖参数估计、假设检验、置信区间、贝叶斯推断、非参数方法及图模型等主要内容。

其优势在于不回避数学本质,但避免陷入复杂证明,重点明确各工具的假设条件、适用场景与局限性。例如在 A/B 实验中,不仅讲解 p p p-value 计算,更引导读者思考实验数据是否满足假设、样本量是否充足、效应量大小等关键问题,为实际业务决策提供完整逻辑框架。
3. 优化理论:Stephen Boyd《Convex Optimization》
优化理论是理解机器学习算法原理的关键。逻辑回归的 Sigmoid 函数选择、SVM 的最大间隔原理、深度学习中各类梯度下降优化器的设计,本质均是优化问题------定义损失函数后,在约束条件下寻找最优参数。

该书内容全面且逻辑清晰,虽无需逐页通读,但可作为"工具字典"随时查阅。它能帮助读者打破算法"黑盒认知",将各类模型视为不同场景下的优化解决方案,建立统一的算法思维框架。
实践建议
理论学习需结合实践落地,方能深化理解:
- 学习线性代数时,基于 Python 和 Numpy 手动实现 SVD、PCA,在代码调试中强化对子空间、正交基等概念的认知;
- 学习概率统计时,利用公开数据集完成完整 A/B 实验分析,或实现简单贝叶斯分类器(如垃圾邮件分类),深化对置信区间、 p p p-value 的理解;
- 学习优化理论时,从基础梯度下降法入手,手动实现直线拟合,再结合 PyTorch、TensorFlow 源码,理解复杂优化器的设计逻辑。
补充资源
- 视频资源:3Blue1Brown《线性代数的本质》系列,以几何直觉为核心,与 Strang 著作搭配学习可大幅提升效果,视频地址:【官方双语/合集】线性代数的本质 - 系列合集;
- 配套笔记:3Blue1Brown 线性代数中英文笔记,补充视频中省略的推导细节与背景知识,可搭配《线性代数的几何意义》(西安电子科技大学版)使用;
- 基础铺垫:若直接阅读上述外文著作存在难度,可先通过同济《高等数学》、清华《线性代数》、浙大《概率论与数理统计》夯实基础;
- 进阶读物:当基础扎实后,可挑战《The Elements of Statistical Learning (ESL)》,该书被誉为算法岗"毕业论文",配套资源含中文翻译、代码实现及习题解答(附 764 页 PDF)。
二、数学系视角的经典教材推荐(Yuhang Liu 分享)
Yuhang Liu 编辑于 2018-12-19 12:18
本科阶段的优质数学书涵盖多个分支,以下为不同领域的经典入门与进阶著作:
1. 数论入门:Apostol《Intro to Analytic Number Theory》
该书条理清晰且自成体系,无需深厚前置知识,大二学生即可跟进学习(未学复变函数可跳过素数定理证明章节),是入门现代数论的优质读物。

2. 几何拓扑类
- 《From Calculus to Cohomology》:几何拓扑入门必备,覆盖基础常识;
- John Lee《Intro to Smooth Manifolds》与 Spivak《A Comprehensive Introduction to Differential Geometry》:内容详尽,对初学者友好,但篇幅偏长、细节冗余;
- Milnor《微分观点下的拓扑》:经典著作,受写作时代限制,部分内容深度不足;
- Milnor《Characteristic Classes》《Morse Theory》:对应领域入门经典,虽不够全面,但主要知识点讲解透彻;
- Bott-Tu《Differential Forms in Algebraic Topology》:谱序列章节讲解友好,适合未系统学习同调代数的读者;
- Narasimhan《Compact Riemann Surfaces》:100 余页的小册子,涵盖层上同调计算、黎曼 - 罗赫定理等重要内容,入门门槛适中。
三、数学分析与实分析优质著作(数学人生、tepid 分享)
tepid \quad \; 2018-12-30 19:54
数学人生 2020-03-26 07:42
数学分析作为数学系的重要课程,优质教材可分为国内与国外两类,实分析领域也有诸多经典著作值得推荐:
1. 数学分析教材
(1)国内著作
- 徐森林《数学分析》:1200 页篇幅,兼具高观点与详尽性,涵盖 R n \mathbb{R}^n Rn 拓扑与微分形式积分,例题丰富且习题梯度平滑,配套习题解答可避免闭门造车,思考题包含常、史教材中的难题;
- 梅加强《数学分析》:600 页浓缩主要内容,文笔清晰、记号友好、排版美观,习题由浅入深,对流形与微分形式积分有基础介绍,适合快速掌握国内院校数分主要要求;
- 其他点评:陈天权著作内容拼接感强,体系性不足,但习题分小问引导的设计值得借鉴;王昆扬著作跳过黎曼积分直接讲解勒贝格积分,适合无考试压力、追求进阶视角的读者。
(2)国外著作
- 卓里奇《数学分析》:第二卷拓扑与赋范线性空间章节精彩,覆盖国内数分全部内容,但极限、求导部分叙述冗余,一致收敛与级数章节逻辑不够清晰;
- Browder《An introduction to mathematical analysis》:300 页篇幅涵盖测度与积分,欧式空间流形积分章节讲解精炼,适合具备基础计算能力的读者;
- Herbert Amann《Analysis》三部曲:内容全面但体量庞大,对毅力要求较高;
- Goldment《Analysis》四卷本:叙述风格松散,主线不够明确,阅读体验欠佳;
- Rudin《数学分析原理》:从度量空间切入简化证明,但多元部分讲解较薄弱,计算类例题不足。
2. 实分析教材
- Bogachev《实分析》:需具备较好拓扑基础,正文简洁但补充内容丰富,习题难度极高,部分题目需查阅参考资料,是概率领域的标准参考读物;
- Richard Bass《Real Analysis for Graduate Students》:难度友好,后续章节涵盖奇异积分相关内容,适合入门实分析;
- Dibenedetto《Real Analysis》(第一版):450 页覆盖 PDE 所需实分析主要内容,但部分证明跳跃、叙述不够清晰,需搭配其他教材补充。
3. 泛函分析教材
Dietmar Salamon《Functional Analysis》:叙述清晰,部分细节偏冗余,以通用框架处理各类主题,体系完整,习题设计具有启发性。
4. 科普与方法类书籍
- 《思考的乐趣:Matrix67 数学笔记》:以短篇形式讲解数学定理、技巧与趣味故事,适合碎片化阅读;
- 《数学与生活》:用通俗语言与实例讲解中小学至本科阶段数学知识,降低晦涩概念理解门槛;
- 《魔鬼数学》:结合大数据场景解读数学应用,展现数学在现实中的价值;
- 《数学之美》:以互联网与大数据为背景,介绍数学思想的实际应用,适合大数据入门读者;
- 《陶哲轩教你学数学》:菲尔兹奖得主分享数学竞赛技巧与解题思路;
- 《怎样解题》:Polya 著作,以教学案例为载体,讲解数学学习与教学方法;
- 《一个数学家的辩白》:G.H.Hardy 经典作品,展现数学家的思维与情怀;
- 《古今数学思想》:梳理数学发展脉络,兼具知识性与趣味性。
四、经典重温与进阶升华类著作(xyor wz 分享)
齐民友《重温微积分》是对个人影响深远的著作,虽书名聚焦微积分,但内容覆盖多个进阶领域,适合学过基础微积分后进一步深化理解的读者。
1. 书籍特点
- 内容体系:涵盖变量数学基础、函数、微分学、积分学、傅里叶级数与积分、数学基础(实数理论、度量空间等)、微分流形上的微积分等,目录逻辑清晰,从基础到进阶层层递进;
- 叙述风格:循循善诱,兼顾直观理解与理论深度,无需深厚前置知识,学过基本微积分即可阅读,可系统精读或碎片化翻阅;
- 价值体现:衔接古典微积分与现代数学,以"外微分形式""Stokes 公式"等内容为桥梁,展现微积分的本质与延伸,揭示数学与物理学的内在关联。
2. 推荐理由
该书 2004 年出版,序中明确其定位------为读过一次微积分、希望进一步学习现代数学的读者而写。书中对黎曼积分的历史背景与局限性、勒贝格积分的重要思想等内容的探讨,能帮助读者建立更深刻的数学认知,是"温故而知新"的典范。
补充推荐
- 代数领域:黎景辉《高等线性代数学》,与《重温微积分》具有类似的升华作用;
- 几何与拓扑领域:古志鸣《几何与拓扑的概念导引》,适合深化几何拓扑知识理解。
【笔记】3Blue1Brown 线性代数的本质
赛维勒的理发师 编辑于 2022-03-20 21:18
00 序言
对于线性代数这一学科,目标是建立正确的几何直观。
01 向量究竟是什么
引入一些数作为坐标是一种鲁莽的行为。------赫尔曼·外尔
三种看待向量的观点
| 物理专业的学生 | 空间中的箭头(具备长度与方向) |
|---|---|
| 计算机专业的学生 | 有序的数字列表 |
| 数学家 | 满足特定运算规则的任意对象(前两种观点的统一) |
向量的运算
线性代数的理论体系围绕两种基本运算展开:向量加法 和向量数乘。
| 运算类型 | 物理观点 | 列表观点 |
|---|---|---|
| 向量加法 | 描述空间中的平移运动 | 对应分量依次相加 |
| 向量数乘 | 对向量进行长度缩放(标量的作用) | 各分量与标量分别相乘 |
02 线性组合、张成的空间与基
例: [ 3 − 2 ] = 3 i ^ + ( − 2 ) j ^ \begin{bmatrix} 3\\-2 \end{bmatrix} = 3\hat{i} + (-2)\hat{j} [3−2]=3i^+(−2)j^
概念定义
- 基向量 : i ^ , j ^ \hat{i},\hat{j} i^,j^ 被称为基向量,是线性变换中缩放操作的基本对象。
- 线性组合 :形如 a v ⃗ + b w ⃗ a\vec{v} + b\vec{w} av +bw (其中 a , b a,b a,b 为标量)的表达式,称为向量 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 的线性组合。
- 张成的空间 :所有可表示为给定向量线性组合的向量构成的集合,记为 { a v ⃗ + b w ⃗ ∣ a , b ∈ R } \left\{ a\vec{v} + b\vec{w} \mid a,b \in \mathbb{R} \right\} {av +bw ∣a,b∈R},称为给定向量张成的空间。
- 线性相关 :若存在部分向量,移除后不改变原向量组张成的空间,则称该向量组是线性相关的。
- 线性无关 :若向量组中所有向量均能为张成的空间增加新维度(即任一向量不能表示为其他向量的线性组合,如 u ⃗ ≠ a v ⃗ + b w ⃗ \vec{u} \ne a\vec{v} + b\vec{w} u =av +bw ),则称该向量组是线性无关的。
- 向量空间的基 :张成向量空间的线性无关向量组,称为该向量空间的一组基。
不同维度下的张成空间
二维空间
| 给定的二维向量组 | 张成的空间 |
|---|---|
| 两个不共线的二维向量 | 全体二维向量构成的集合 |
| 两个共线的二维向量 | 一条直线上的所有向量 |
| 两个零向量 | 仅包含原点的单点集合 |
三维空间
| 给定的三维向量组 | 张成的空间 |
|---|---|
| 两个不共线的三维向量 | 过坐标原点的平面 |
| 三个向量(第三个向量落在前两个向量张成的平面内) | 该平面本身 |
| 三个不共面的三维向量 | 全体三维向量构成的空间(平面扫动形成) |
03 矩阵与线性变换
定义
- 变换:本质是"函数"的几何表述,特指输入与输出均为向量的映射关系,暗示以"运动"视角分析。
- 线性变换:满足两个条件的变换:① 任意直线经变换后仍为直线;② 坐标原点保持不变(等价于网格线保持平行且等距分布)。
矩阵与线性变换的关联
- 二维线性变换可由基向量 i ^ , j ^ \hat{i},\hat{j} i^,j^ 的变换结果完全确定,变换后的基向量构成矩阵的列。
- 2×2 矩阵 [ a b c d ] \begin{bmatrix} a&b\\ c&d \end{bmatrix} [acbd] 的几何意义: i ^ \hat{i} i^ 变换后为 [ a c ] \begin{bmatrix} a\\ c \end{bmatrix} [ac], j ^ \hat{j} j^ 变换后为 [ b d ] \begin{bmatrix} b\\ d \end{bmatrix} [bd]。
- 向量经线性变换的计算:对任意向量 [ x y ] \begin{bmatrix} x\\ y \end{bmatrix} [xy],其变换结果为 x [ a c ] + y [ b d ] x\begin{bmatrix} a\\ c \end{bmatrix} + y\begin{bmatrix} b\\ d \end{bmatrix} x[ac]+y[bd],即矩阵与向量的乘积:
a b c d \] \[ x y \] = \[ a x + b y c x + d y \] \\begin{bmatrix} a\&b\\\\ c\&d \\end{bmatrix} \\begin{bmatrix} x\\\\ y \\end{bmatrix} = \\begin{bmatrix} ax + by\\\\ cx + dy \\end{bmatrix} \[acbd\]\[xy\]=\[ax+bycx+dy
例:变换矩阵 [ 3 2 − 2 1 ] \begin{bmatrix} 3&2\\ -2&1 \end{bmatrix} [3−221] 作用于向量 [ 5 7 ] \begin{bmatrix} 5\\ 7 \end{bmatrix} [57] 的结果为:
5 [ 3 − 2 ] + 7 [ 2 1 ] = [ 29 − 3 ] 5\begin{bmatrix} 3\\ -2 \end{bmatrix} + 7\begin{bmatrix} 2\\ 1 \end{bmatrix} = \begin{bmatrix} 29\\ -3 \end{bmatrix} 5[3−2]+7[21]=[29−3]
04 矩阵乘法与线性变换复合
矩阵乘法的几何意义
两个矩阵相乘表示两个线性变换的相继作用,结果矩阵称为"复合矩阵"。
例:旋转矩阵 [ 0 − 1 1 0 ] \begin{bmatrix} 0&-1\\ 1&0 \end{bmatrix} [01−10] 与剪切矩阵 [ 1 1 0 1 ] \begin{bmatrix} 1&1\\ 0&1 \end{bmatrix} [1011] 的复合运算:
1 1 0 1 \] \[ 0 − 1 1 0 \] = \[ 1 − 1 1 0 \] \\begin{bmatrix} 1\&1\\\\ 0\&1 \\end{bmatrix} \\begin{bmatrix} 0\&-1\\\\ 1\&0 \\end{bmatrix} = \\begin{bmatrix} 1\&-1\\\\ 1\&0 \\end{bmatrix} \[1011\]\[01−10\]=\[11−10
表示先进行旋转变换,再进行剪切变换。
矩阵乘法的运算规则
- 一般形式:对于矩阵 M 1 = [ a b c d ] M_1 = \begin{bmatrix} a&b\\ c&d \end{bmatrix} M1=[acbd] 与 M 2 = [ e f g h ] M_2 = \begin{bmatrix} e&f\\ g&h \end{bmatrix} M2=[egfh],乘积为:
M 2 M 1 = [ a e + b g a f + b h c e + d g c f + d h ] M_2 M_1 = \begin{bmatrix} ae + bg&af + bh\\ ce + dg&cf + dh \end{bmatrix} M2M1=[ae+bgce+dgaf+bhcf+dh] - 关键性质:
- 不满足交换律: M 1 M 2 ≠ M 2 M 1 M_1 M_2 \ne M_2 M_1 M1M2=M2M1(变换顺序影响结果)。
- 满足结合律: ( A B ) C = A ( B C ) (AB)C = A(BC) (AB)C=A(BC)(变换的相继作用与分组无关)。
例:计算 M 2 M 1 M_2 M_1 M2M1 时,需先确定 M 1 M_1 M1 对基向量的变换,再将结果作为 M 2 M_2 M2 的输入,最终变换结果构成复合矩阵的列。
附注 1 三维空间中的线性变换
三维空间的线性变换由 3×3 矩阵描述,矩阵的列对应基向量 i ^ , j ^ , k ^ \hat{i},\hat{j},\hat{k} i^,j^,k^ 经变换后的结果。其性质(如变换的线性性、矩阵与变换的一一对应)与二维空间一致,仅维度扩展至三维。
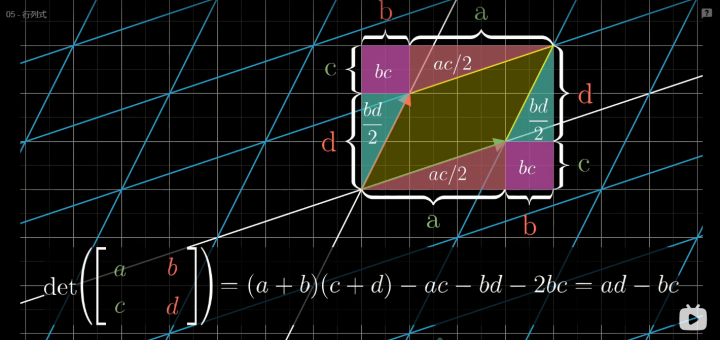
05 行列式
行列式的几何意义
行列式 是线性变换中面积(或体积)的缩放比例(因网格线平行等距,缩放比例对任意图形一致)。
行列式的关键性质
- 符号意义:行列式为正,空间取向保持不变;行列式为负,空间取向翻转(二维为平面翻转,三维为右手系变为左手系)。
- 特殊值含义:行列式为 0 时,变换将空间压缩至更低维度(二维压缩为直线或点,三维压缩为平面、直线或点)。
行列式的计算方法
- 二阶行列式: det ( [ a b c d ] ) = a d − b c \det\left( \begin{bmatrix} a&b\\ c&d \end{bmatrix} \right) = ad - bc det([acbd])=ad−bc。
- 三阶行列式(按第一行展开):
det ( [ a b c d e f g h i ] ) = a det ( [ e f h i ] ) − b det ( [ d f g i ] ) + c det ( [ d e g h ] ) \det\left( \begin{bmatrix} a&b&c\\ d&e&f\\ g&h&i \end{bmatrix} \right) = a\det\left( \begin{bmatrix} e&f\\ h&i \end{bmatrix} \right) - b\det\left( \begin{bmatrix} d&f\\ g&i \end{bmatrix} \right) + c\det\left( \begin{bmatrix} d&e\\ g&h \end{bmatrix} \right) det adgbehcfi =adet([ehfi])−bdet([dgfi])+cdet([dgeh])
例: det ( [ 3 2 0 2 ] ) = 3 × 2 − 2 × 0 = 6 \det\left( \begin{bmatrix} 3&2\\ 0&2 \end{bmatrix} \right) = 3×2 - 2×0 = 6 det([3022])=3×2−2×0=6,表示该变换将平面图形面积放大 6 倍。
06 逆矩阵、列空间与零空间
线性方程组的向量形式
线性方程组 { 2 x + 5 y + 3 z = − 3 4 x + 0 y + 8 z = 0 1 x + 3 y + 0 z = 2 \begin{cases} 2x + 5y + 3z = -3\\ 4x + 0y + 8z = 0\\ 1x + 3y + 0z = 2 \end{cases} ⎩ ⎨ ⎧2x+5y+3z=−34x+0y+8z=01x+3y+0z=2 可表示为矩阵向量方程:
A x ⃗ = v ⃗ A\vec{x} = \vec{v} Ax =v
其中 A = [ 2 5 3 4 0 8 1 3 0 ] A = \begin{bmatrix} 2&5&3\\ 4&0&8\\ 1&3&0 \end{bmatrix} A= 241503380 (系数矩阵), x ⃗ = [ x y z ] \vec{x} = \begin{bmatrix} x\\ y\\ z \end{bmatrix} x = xyz (未知数向量), v ⃗ = [ − 3 0 2 ] \vec{v} = \begin{bmatrix} -3\\ 0\\ 2 \end{bmatrix} v = −302 (常数向量)。
几何解释与方程求解
- 方程的几何意义:寻找向量 x ⃗ \vec{x} x ,使其经矩阵 A A A 对应的线性变换后,与向量 v ⃗ \vec{v} v 重合。
- 有解条件与求解方法:
- 当 det ( A ) ≠ 0 \det(A) \ne 0 det(A)=0(变换为满秩):存在唯一逆矩阵 A − 1 A^{-1} A−1,满足 A − 1 A = I A^{-1}A = I A−1A=I( I I I 为单位矩阵),解为 x ⃗ = A − 1 v ⃗ \vec{x} = A^{-1}\vec{v} x =A−1v 。
- 当 det ( A ) = 0 \det(A) = 0 det(A)=0(变换为降秩):逆矩阵不存在,方程可能有解(取决于 v ⃗ \vec{v} v 是否在 A A A 的列空间中)。
概念定义
- 列空间 :所有可能的输出向量 A x ⃗ A\vec{x} Ax 构成的集合,即矩阵列向量张成的空间。
- 秩 :列空间的维数,代表变换后空间的维度;秩等于矩阵列数时,称为满秩。
- 零空间(核) :变换后映射到原点的所有向量构成的集合;对于方程 A x ⃗ = 0 ⃗ A\vec{x} = \vec{0} Ax =0 ,零空间即为其所有解的集合。
总结
线性方程组的求解可通过线性变换视角分析:逆矩阵对应逆变换(满秩时唯一解),列空间决定解的存在性,零空间描述齐次方程的解结构。
附注 2 非方阵
非方阵的几何含义
非方阵表示不同维度空间之间的线性变换。
例:3×2 矩阵 [ 2 0 − 1 1 − 2 1 ] \begin{bmatrix} 2&0\\ -1&1\\ -2&1 \end{bmatrix} 2−1−2011 表示从二维空间到三维空间的映射:
- 二维基向量 i ^ \hat{i} i^ 变换为三维向量 [ 2 − 1 − 2 ] \begin{bmatrix} 2\\ -1\\ -2 \end{bmatrix} 2−1−2 。
- 二维基向量 j ^ \hat{j} j^ 变换为三维向量 [ 0 1 1 ] \begin{bmatrix} 0\\ 1\\ 1 \end{bmatrix} 011 。
该变换为满秩变换(秩等于输入空间维度 2),其列空间为三维空间中的一个平面。

07 点积与对偶性
卡尔文:你知道吗,我觉得数学不是一门科学,而是一种宗教。
霍布斯:一种宗教?
卡尔文:是啊。这些公式就像奇迹一般。你取出两个数,把它们相加时,他们神奇地成为了一个全新的数!没人能说清这到底是怎么发生的。你要么完全相信,要么完全不信。
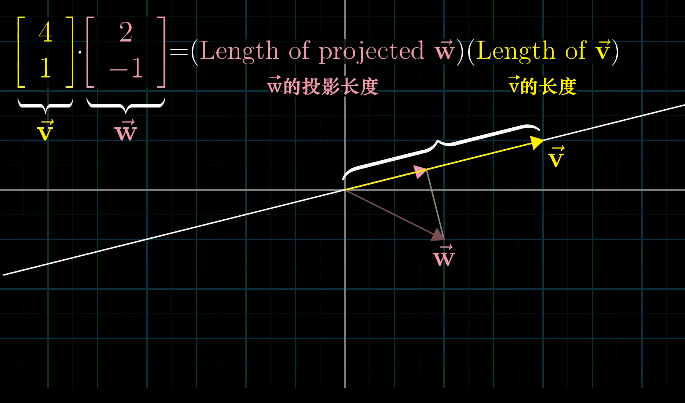
点积的定义与几何意义
- 代数定义:对于向量 v ⃗ = [ v 1 v 2 ] \vec{v} = \begin{bmatrix} v_1\\ v_2 \end{bmatrix} v =[v1v2] 与 w ⃗ = [ w 1 w 2 ] \vec{w} = \begin{bmatrix} w_1\\ w_2 \end{bmatrix} w =[w1w2],点积为 v ⃗ ⋅ w ⃗ = v 1 w 1 + v 2 w 2 \vec{v} \cdot \vec{w} = v_1 w_1 + v_2 w_2 v ⋅w =v1w1+v2w2。
- 几何意义: v ⃗ ⋅ w ⃗ = ∥ v ⃗ ∥ ∥ w ⃗ ∥ cos θ \vec{v} \cdot \vec{w} = \|\vec{v}\| \|\vec{w}\| \cos\theta v ⋅w =∥v ∥∥w ∥cosθ,其中 θ \theta θ 为两向量的夹角,即一个向量在另一个向量方向上的投影长度与被投影向量长度的乘积。
点积的交换律证明
- 若 ∥ v ⃗ ∥ = ∥ w ⃗ ∥ \|\vec{v}\| = \|\vec{w}\| ∥v ∥=∥w ∥:利用对称性, v ⃗ \vec{v} v 在 w ⃗ \vec{w} w 上的投影与 w ⃗ \vec{w} w 在 v ⃗ \vec{v} v 上的投影相等,故点积相等。
- 若 ∥ v ⃗ ∥ ≠ ∥ w ⃗ ∥ \|\vec{v}\| \ne \|\vec{w}\| ∥v ∥=∥w ∥:设 v ⃗ ′ = k v ⃗ \vec{v}' = k\vec{v} v ′=kv ( k k k 为标量),则 v ⃗ ′ ⋅ w ⃗ = k ( v ⃗ ⋅ w ⃗ ) \vec{v}' \cdot \vec{w} = k(\vec{v} \cdot \vec{w}) v ′⋅w =k(v ⋅w ),无论将 k k k 视为对 v ⃗ \vec{v} v 的缩放还是对投影长度的缩放,结果一致,故交换律成立。
点积与对偶性
- 对偶性:多维空间到一维空间(数轴)的线性变换,与该空间中的一个向量一一对应,即"应用线性变换"等价于"与该向量做点积",该向量称为变换的对偶向量。
- 具体推导:
- 设数轴单位向量为 u ^ = [ u x u y ] \hat{u} = \begin{bmatrix} u_x\\ u_y \end{bmatrix} u^=[uxuy],二维空间到该数轴的线性变换为 [ u x u y ] \begin{bmatrix} u_x&u_y \end{bmatrix} [uxuy]。
- 对任意向量 [ x y ] \begin{bmatrix} x\\ y \end{bmatrix} [xy],变换结果为 [ u x u y ] [ x y ] = u x x + u y y \begin{bmatrix} u_x&u_y \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = u_x x + u_y y [uxuy][xy]=uxx+uyy,与点积 u ^ ⋅ [ x y ] \hat{u} \cdot \begin{bmatrix} x\\ y \end{bmatrix} u^⋅[xy] 完全等价。
- 推广至非单位向量:结合缩放性质,结论依然成立,即线性变换与点积的对偶关系普遍存在。
08 介绍
第一部分-叉积的标准介绍
二维叉积
- 定义:对于二维向量 v ⃗ = [ v 1 v 2 ] \vec{v} = \begin{bmatrix} v_1\\ v_2 \end{bmatrix} v =[v1v2] 与 w ⃗ = [ w 1 w 2 ] \vec{w} = \begin{bmatrix} w_1\\ w_2 \end{bmatrix} w =[w1w2],叉积 v ⃗ × w ⃗ \vec{v} \times \vec{w} v ×w 的数值等于两向量张成的平行四边形面积,符号由右手定则确定( v ⃗ \vec{v} v 在 w ⃗ \vec{w} w 右侧为正,左侧为负)。
- 计算方法: v ⃗ × w ⃗ = det ( [ v 1 w 1 v 2 w 2 ] ) = v 1 w 2 − v 2 w 1 \vec{v} \times \vec{w} = \det\left( \begin{bmatrix} v_1&w_1\\ v_2&w_2 \end{bmatrix} \right) = v_1 w_2 - v_2 w_1 v ×w =det([v1v2w1w2])=v1w2−v2w1。
例: v ⃗ = [ − 3 1 ] \vec{v} = \begin{bmatrix} -3\\ 1 \end{bmatrix} v =[−31] 与 w ⃗ = [ 2 1 ] \vec{w} = \begin{bmatrix} 2\\ 1 \end{bmatrix} w =[21] 的叉积为 det ( [ − 3 2 1 1 ] ) = − 3 × 1 − 1 × 2 = − 5 \det\left( \begin{bmatrix} -3&2\\ 1&1 \end{bmatrix} \right) = -3×1 - 1×2 = -5 det([−3121])=−3×1−1×2=−5,面积为 5,符号为负( v ⃗ \vec{v} v 在 w ⃗ \vec{w} w 左侧)。
三维叉积(真正的叉积)
- 定义:由两个三维向量 v ⃗ = [ v 1 v 2 v 3 ] \vec{v} = \begin{bmatrix} v_1\\ v_2\\ v_3 \end{bmatrix} v = v1v2v3 与 w ⃗ = [ w 1 w 2 w 3 ] \vec{w} = \begin{bmatrix} w_1\\ w_2\\ w_3 \end{bmatrix} w = w1w2w3 生成一个新的三维向量 p ⃗ = v ⃗ × w ⃗ \vec{p} = \vec{v} \times \vec{w} p =v ×w ,满足:
- 长度: ∥ p ⃗ ∥ \|\vec{p}\| ∥p ∥ 等于 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形面积。
- 方向:垂直于 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 所在平面,遵循右手定则(四指从 v ⃗ \vec{v} v 转向 w ⃗ \vec{w} w ,拇指指向为 p ⃗ \vec{p} p 方向)。
- 计算方法:
v ⃗ × w ⃗ = det ( [ i ^ v 1 w 1 j ^ v 2 w 2 k ^ v 3 w 3 ] ) = i ^ ( v 2 w 3 − v 3 w 2 ) − j ^ ( v 1 w 3 − v 3 w 1 ) + k ^ ( v 1 w 2 − v 2 w 1 ) \begin{aligned} \vec{v} \times \vec{w} &= \det\left( \begin{bmatrix} \hat{i} & v_1 & w_1 \\ \hat{j} & v_2 & w_2 \\ \hat{k} & v_3 & w_3 \end{bmatrix} \right) \\ &= \hat{i}(v_2 w_3 - v_3 w_2) - \hat{j}(v_1 w_3 - v_3 w_1) + \hat{k}(v_1 w_2 - v_2 w_1) \end{aligned} v ×w =det i^j^k^v1v2v3w1w2w3 =i^(v2w3−v3w2)−j^(v1w3−v3w1)+k^(v1w2−v2w1)
第二部分 以线性变换的眼光看叉积
对偶性的应用
- 前提:三维空间到数轴的线性变换,必然存在唯一的对偶向量,使得该变换等价于与对偶向量的点积。
- 构造线性变换:定义函数 f ( [ x y z ] ) = det ( [ x v 1 w 1 y v 2 w 2 z v 3 w 3 ] ) f\left( \begin{bmatrix} x\\ y\\ z \end{bmatrix} \right) = \det\left( \begin{bmatrix} x&v_1&w_1\\ y&v_2&w_2\\ z&v_3&w_3 \end{bmatrix} \right) f xyz =det xyzv1v2v3w1w2w3 ,其几何意义为:输入向量 [ x y z ] \begin{bmatrix} x\\ y\\ z \end{bmatrix} xyz 与 v ⃗ , w ⃗ \vec{v},\vec{w} v ,w 张成的平行六面体的有向体积(符号由右手定则确定)。
- 线性性验证:该函数满足线性变换的两条性质(可加性、齐次性),因此可表示为矩阵与向量的乘积,进而等价于与某一对偶向量 p ⃗ \vec{p} p 的点积,即 f ( [ x y z ] ) = p ⃗ ⋅ [ x y z ] f\left( \begin{bmatrix} x\\ y\\ z \end{bmatrix} \right) = \vec{p} \cdot \begin{bmatrix} x\\ y\\ z \end{bmatrix} f xyz =p ⋅ xyz 。
对偶向量与叉积的关系
- 代数推导:将行列式展开, f ( [ x y z ] ) = x ( v 2 w 3 − v 3 w 2 ) + y ( v 3 w 1 − v 1 w 3 ) + z ( v 1 w 2 − v 2 w 1 ) f\left( \begin{bmatrix} x\\ y\\ z \end{bmatrix} \right) = x(v_2 w_3 - v_3 w_2) + y(v_3 w_1 - v_1 w_3) + z(v_1 w_2 - v_2 w_1) f xyz =x(v2w3−v3w2)+y(v3w1−v1w3)+z(v1w2−v2w1),与点积公式 p ⃗ ⋅ [ x y z ] = p 1 x + p 2 y + p 3 z \vec{p} \cdot \begin{bmatrix} x\\ y\\ z \end{bmatrix} = p_1 x + p_2 y + p_3 z p ⋅ xyz =p1x+p2y+p3z 对比,可得 p ⃗ = [ v 2 w 3 − v 3 w 2 v 3 w 1 − v 1 w 3 v 1 w 2 − v 2 w 1 ] \vec{p} = \begin{bmatrix} v_2 w_3 - v_3 w_2\\ v_3 w_1 - v_1 w_3\\ v_1 w_2 - v_2 w_1 \end{bmatrix} p = v2w3−v3w2v3w1−v1w3v1w2−v2w1 ,即 p ⃗ = v ⃗ × w ⃗ \vec{p} = \vec{v} \times \vec{w} p =v ×w 。
- 几何解释:
- 对偶向量 p ⃗ \vec{p} p 需垂直于 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 所在平面(否则平行六面体体积与投影无关)。
- p ⃗ \vec{p} p 的长度需等于 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形面积(体积 = 底面积 × 高,高为输入向量在 p ⃗ \vec{p} p 方向的投影长度)。
- 符号与右手定则一致(确保体积符号与点积结果匹配)。
总结
叉积的本质是:三维空间中"由两个向量构造垂直向量"的运算,可通过"线性变换的对偶性"推导得出。其几何性质(垂直方向、长度等于面积)是线性变换与对偶向量对应关系的必然结果。
09 基变换
坐标系与基向量
- 坐标系定义:向量与一组有序数之间的一一对应关系,称为坐标系。
- 基向量 :坐标系中一组线性无关的向量,用于表示空间中所有向量(如标准坐标系的基向量 i ^ = [ 1 0 ] \hat{i} = \begin{bmatrix} 1\\ 0 \end{bmatrix} i^=[10], j ^ = [ 0 1 ] \hat{j} = \begin{bmatrix} 0\\ 1 \end{bmatrix} j^=[01])。
基变换的逻辑
基向量可视为描述向量的"语言",基变换即不同"语言"之间的转换。
向量在不同基下的表示转换
- 设标准基为 { i ^ , j ^ } \{\hat{i},\hat{j}\} {i^,j^},新基为 { b 1 ⃗ , b 2 ⃗ } \{\vec{b_1},\vec{b_2}\} {b1 ,b2 },其中 b 1 ⃗ = [ 2 1 ] \vec{b_1} = \begin{bmatrix} 2\\ 1 \end{bmatrix} b1 =[21], b 2 ⃗ = [ − 1 1 ] \vec{b_2} = \begin{bmatrix} -1\\ 1 \end{bmatrix} b2 =[−11]。
- 新基到标准基的转换矩阵: B = [ b 1 ⃗ b 2 ⃗ ] = [ 2 − 1 1 1 ] B = \begin{bmatrix} \vec{b_1}&\vec{b_2} \end{bmatrix} = \begin{bmatrix} 2&-1\\ 1&1 \end{bmatrix} B=[b1 b2 ]=[21−11]。
- 若向量在新基下的坐标为 [ x ′ y ′ ] \begin{bmatrix} x'\\ y' \end{bmatrix} [x′y′],则其在标准基下的坐标为 B [ x ′ y ′ ] = x ′ b 1 ⃗ + y ′ b 2 ⃗ B \begin{bmatrix} x'\\ y' \end{bmatrix} = x'\vec{b_1} + y'\vec{b_2} B[x′y′]=x′b1 +y′b2 。
- 例:新基下坐标 [ − 1 2 ] \begin{bmatrix} -1\\ 2 \end{bmatrix} [−12] 对应的标准基坐标为 [ 2 − 1 1 1 ] [ − 1 2 ] = [ − 4 1 ] \begin{bmatrix} 2&-1\\ 1&1 \end{bmatrix} \begin{bmatrix} -1\\ 2 \end{bmatrix} = \begin{bmatrix} -4\\ 1 \end{bmatrix} [21−11][−12]=[−41]。
- 标准基到新基的转换:需用逆矩阵 B − 1 B^{-1} B−1,即向量在新基下的坐标为 B − 1 × B^{-1} \times B−1× 标准基坐标。
线性变换在不同基下的表示转换
- 问题:标准基下的变换矩阵为 M M M,如何求新基下的变换矩阵 M ′ M' M′?
- 转换公式: M ′ = B − 1 M B M' = B^{-1}MB M′=B−1MB,其中 B B B 为新基到标准基的转换矩阵。
- 几何意义:
- B B B:将新基向量转换为标准基向量("翻译"为标准语言)。
- M M M:在标准基下执行线性变换("处理"向量)。
- B − 1 B^{-1} B−1:将变换结果转换回新基向量("翻译"回新语言)。
例:标准基下的 90° 旋转矩阵 M = [ 0 − 1 1 0 ] M = \begin{bmatrix} 0&-1\\ 1&0 \end{bmatrix} M=[01−10],新基 { b 1 ⃗ , b 2 ⃗ } \{\vec{b_1},\vec{b_2}\} {b1 ,b2 } 下的变换矩阵为:
M ′ = B − 1 M B = [ 2 − 1 1 1 ] − 1 [ 0 − 1 1 0 ] [ 2 − 1 1 1 ] M' = B^{-1}MB = \begin{bmatrix} 2&-1\\ 1&1 \end{bmatrix}^{-1} \begin{bmatrix} 0&-1\\ 1&0 \end{bmatrix} \begin{bmatrix} 2&-1\\ 1&1 \end{bmatrix} M′=B−1MB=[21−11]−1[01−10][21−11]
10 特征向量与特征值
定义
对于矩阵 A A A,若存在非零向量 v ⃗ \vec{v} v 和标量 λ \lambda λ,满足 A v ⃗ = λ v ⃗ A\vec{v} = \lambda\vec{v} Av =λv ,则称 v ⃗ \vec{v} v 为 A A A 的特征向量 , λ \lambda λ 为对应的特征值。
- 几何意义:特征向量经线性变换后,仅发生长度缩放(缩放比例为 λ \lambda λ),方向保持不变( λ > 0 \lambda > 0 λ>0)或反向( λ < 0 \lambda < 0 λ<0)。
- 等价形式: A v ⃗ = λ I v ⃗ ⟹ ( A − λ I ) v ⃗ = 0 ⃗ A\vec{v} = \lambda I \vec{v} \implies (A - \lambda I)\vec{v} = \vec{0} Av =λIv ⟹(A−λI)v =0 ,其中 I I I 为单位矩阵。
特征值与特征向量的求解
- 存在非零解的条件:矩阵 A − λ I A - \lambda I A−λI 为奇异矩阵(降秩),即 det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0(特征方程)。
- 求解步骤:
- 解特征方程 det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0,得到特征值 λ \lambda λ。
- 对每个 λ \lambda λ,解齐次线性方程组 ( A − λ I ) v ⃗ = 0 ⃗ (A - \lambda I)\vec{v} = \vec{0} (A−λI)v =0 ,得到对应的特征向量 v ⃗ \vec{v} v 。
例:二维旋转 90° 矩阵 [ 0 − 1 1 0 ] \begin{bmatrix} 0&-1\\ 1&0 \end{bmatrix} [01−10] 的特征方程为 det ( [ − λ − 1 1 − λ ] ) = λ 2 + 1 = 0 \det\left( \begin{bmatrix} -\lambda&-1\\ 1&-\lambda \end{bmatrix} \right) = \lambda^2 + 1 = 0 det([−λ1−1−λ])=λ2+1=0,无实数解,因此该变换无实特征向量。
特征基与矩阵对角化
对角矩阵的特性
对角矩阵(如 [ − 1 0 0 2 ] \begin{bmatrix} -1&0\\ 0&2 \end{bmatrix} [−1002])具有以下特殊性质:
- 其基向量均为特征向量,对角元素即为对应的特征值;
- 幂运算简便,即 [ λ 1 0 0 λ 2 ] n = [ λ 1 n 0 0 λ 2 n ] \begin{bmatrix} \lambda_1&0\\ 0&\lambda_2 \end{bmatrix}^n = \begin{bmatrix} \lambda_1^n&0\\ 0&\lambda_2^n \end{bmatrix} [λ100λ2]n=[λ1n00λ2n],仅需对主对角线元素分别取 n n n 次幂。
特征基的定义
由一组特征向量作为基向量所构成的集合,称为特征基。
矩阵对角化的定义与条件
- 定义 :若存在可逆矩阵 P P P(其列向量为矩阵 A A A 的特征向量)和对角矩阵 Λ \Lambda Λ(其对角元素为 A A A 的对应特征值),使得 A = P Λ P − 1 A = P\Lambda P^{-1} A=PΛP−1,则称矩阵 A A A 可对角化。
- 条件 :矩阵 A A A 可对角化的充要条件是, A A A 拥有 n n n 个线性无关的特征向量(即这些特征向量能够张成整个空间,构成一组特征基)。
对角化的应用:简化矩阵幂运算
若矩阵 A A A 可对角化,则其 n n n 次幂可通过以下公式简化计算:
A n = P Λ n P − 1 A^n = P\Lambda^n P^{-1} An=PΛnP−1
其中, Λ n \Lambda^n Λn 为对角矩阵 Λ \Lambda Λ 的 n n n 次幂,仅需对 Λ \Lambda Λ 的主对角线元素分别取 n n n 次幂即可得到。
实例:计算矩阵 A = [ 3 1 0 2 ] A = \begin{bmatrix} 3&1\\ 0&2 \end{bmatrix} A=[3012] 的 100 次幂
-
求特征值与特征向量:
-
解特征方程 det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0,即 ∣ 3 − λ 1 0 2 − λ ∣ = ( 3 − λ ) ( 2 − λ ) = 0 \begin{vmatrix} 3 - \lambda & 1 \\ 0 & 2 - \lambda \end{vmatrix} = (3 - \lambda)(2 - \lambda) = 0 3−λ012−λ =(3−λ)(2−λ)=0,得特征值 λ 1 = 3 \lambda_1 = 3 λ1=3, λ 2 = 2 \lambda_2 = 2 λ2=2。
-
对 λ 1 = 3 \lambda_1 = 3 λ1=3,解 ( A − 3 I ) v ⃗ = 0 (A - 3I)\vec{v} = 0 (A−3I)v =0,得特征向量 v 1 ⃗ = [ 1 0 ] \vec{v_1} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} v1 =[10];
对 λ 2 = 2 \lambda_2 = 2 λ2=2,解 ( A − 2 I ) v ⃗ = 0 (A - 2I)\vec{v} = 0 (A−2I)v =0,得特征向量 v 2 ⃗ = [ − 1 1 ] \vec{v_2} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} v2 =[−11]。
-
-
构建变换矩阵及其逆矩阵:
- 特征基变换矩阵 P P P 由特征向量构成: P = [ 1 − 1 0 1 ] P = \begin{bmatrix} 1&-1\\ 0&1 \end{bmatrix} P=[10−11]。
- 求 P P P 的逆矩阵: P − 1 = [ 1 1 0 1 ] P^{-1} = \begin{bmatrix} 1&1\\ 0&1 \end{bmatrix} P−1=[1011]。
-
矩阵对角化 :
Λ = P − 1 A P = [ 1 1 0 1 ] [ 3 1 0 2 ] [ 1 − 1 0 1 ] = [ 3 0 0 2 ] \Lambda = P^{-1}AP = \begin{bmatrix} 1&1\\ 0&1 \end{bmatrix} \begin{bmatrix} 3&1\\ 0&2 \end{bmatrix} \begin{bmatrix} 1&-1\\ 0&1 \end{bmatrix} = \begin{bmatrix} 3&0\\ 0&2 \end{bmatrix} Λ=P−1AP=[1011][3012][10−11]=[3002] -
计算矩阵的 100 次幂:
- 先求对角矩阵的幂: Λ 100 = [ 3 100 0 0 2 100 ] \Lambda^{100} = \begin{bmatrix} 3^{100}&0\\ 0&2^{100} \end{bmatrix} Λ100=[3100002100]。
- 代入公式得原矩阵的幂:
A 100 = P Λ 100 P − 1 = [ 1 − 1 0 1 ] [ 3 100 0 0 2 100 ] [ 1 1 0 1 ] = [ 3 100 3 100 − 2 100 0 2 100 ] A^{100} = P\Lambda^{100}P^{-1} = \begin{bmatrix} 1&-1\\ 0&1 \end{bmatrix} \begin{bmatrix} 3^{100}&0\\ 0&2^{100} \end{bmatrix} \begin{bmatrix} 1&1\\ 0&1 \end{bmatrix} = \begin{bmatrix} 3^{100}&3^{100} - 2^{100}\\ 0&2^{100} \end{bmatrix} A100=PΛ100P−1=[10−11][3100002100][1011]=[310003100−21002100]
说明
并非所有矩阵都可对角化,例如剪切矩阵,因其特征向量无法张成整个空间,不满足对角化条件。

矩阵对角化两个等价关系式
-
对角化标准形式
A = P Λ P − 1 A = P \Lambda P^{-1} A=PΛP−1其中, A A A 为待对角化的原始矩阵, P P P 是以 A A A 的线性无关特征向量为列构成的可逆矩阵, Λ \Lambda Λ 为对角矩阵,其主对角线元素是 A A A 对应的特征值,且特征值的排列顺序与 P P P 中特征向量的排列顺序保持一致。
标准形式明确了对角化的定义:可逆矩阵 P P P 与 P − 1 P^{-1} P−1 构成相似变换,将原始矩阵 A A A 转化为对角矩阵 Λ \Lambda Λ,体现了 A A A 可通过相似变换实现对角化的本质属性。
-
特征基下的表示形式
Λ = P − 1 A P \Lambda = P^{-1} A P Λ=P−1AP该式由标准形式推导得出:对 A = P Λ P − 1 A = P \Lambda P^{-1} A=PΛP−1 两端分别左乘 P − 1 P^{-1} P−1、右乘 P P P,借助 P − 1 P = I P^{-1}P = I P−1P=I(单位矩阵)的性质即可直接推导得到。
表示形式揭示了对角矩阵的几何意义: Λ \Lambda Λ 是矩阵 A A A 在特征向量构成的"特征基"下的矩阵表示,反映了线性变换在特征基下的最简表达形式。
练习:斐波那契数列的矩阵表示
斐波那契数列 { F n } \{F_n\} {Fn} 的定义为: F 0 = 0 F_0 = 0 F0=0 , F 1 = 1 F_1 = 1 F1=1 ,且对任意正整数 n n n ,满足递推关系 F n + 2 = F n + 1 + F n F_{n+2} = F_{n+1} + F_n Fn+2=Fn+1+Fn 。该数列可通过矩阵 A = [ 0 1 1 1 ] A = \begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix} A=[0111] 的幂运算表示,具体如下:
一、矩阵幂与斐波那契数列的关系
猜想 :对任意正整数 n n n ,矩阵 A A A 的 n n n 次幂满足
A n = [ F n − 1 F n F n F n + 1 ] A^n = \begin{bmatrix} F_{n-1} & F_n \\ F_n & F_{n+1} \end{bmatrix} An=[Fn−1FnFnFn+1]
证明(数学归纳法):
-
基例 :当 n = 1 n=1 n=1 时, A 1 = [ 0 1 1 1 ] A^1 = \begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix} A1=[0111] ,此时 F 0 = 0 F_0 = 0 F0=0 , F 1 = 1 F_1 = 1 F1=1 , F 2 = F 1 + F 0 = 1 F_2 = F_1 + F_0 = 1 F2=F1+F0=1 ,等式右边为 [ F 0 F 1 F 1 F 2 ] = [ 0 1 1 1 ] \begin{bmatrix} F_0 & F_1 \\ F_1 & F_2 \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix} [F0F1F1F2]=[0111] ,猜想成立。
-
归纳假设 :假设当 n = k n=k n=k 时猜想成立,即 A k = [ F k − 1 F k F k F k + 1 ] A^k = \begin{bmatrix} F_{k-1} & F_k \\ F_k & F_{k+1} \end{bmatrix} Ak=[Fk−1FkFkFk+1] 。则当 n = k + 1 n=k+1 n=k+1 时:
A k + 1 = A k ⋅ A = [ F k − 1 F k F k F k + 1 ] [ 0 1 1 1 ] = [ F k F k − 1 + F k F k + 1 F k + F k + 1 ] A^{k+1} = A^k \cdot A = \begin{bmatrix} F_{k-1} & F_k \\ F_k & F_{k+1} \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} F_k & F_{k-1} + F_k \\ F_{k+1} & F_k + F_{k+1} \end{bmatrix} Ak+1=Ak⋅A=[Fk−1FkFkFk+1][0111]=[FkFk+1Fk−1+FkFk+Fk+1]根据递推关系 F k + 1 = F k + F k − 1 F_{k+1} = F_k + F_{k-1} Fk+1=Fk+Fk−1 和 F k + 2 = F k + 1 + F k F_{k+2} = F_{k+1} + F_k Fk+2=Fk+1+Fk ,上式可化简为 [ F k F k + 1 F k + 1 F k + 2 ] \begin{bmatrix} F_k & F_{k+1} \\ F_{k+1} & F_{k+2} \end{bmatrix} [FkFk+1Fk+1Fk+2] ,即 n = k + 1 n=k+1 n=k+1 时猜想也成立。
由数学归纳法可知,对所有正整数 n n n ,猜想成立。
二、利用矩阵对角化求斐波那契数列通项公式
-
求矩阵 A A A 的特征值 :
解特征方程 det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0 ,即
∣ − λ 1 1 1 − λ ∣ = λ 2 − λ − 1 = 0 \begin{vmatrix} -\lambda & 1 \\ 1 & 1 - \lambda \end{vmatrix} = \lambda^2 - \lambda - 1 = 0 −λ111−λ =λ2−λ−1=0解得特征值 λ 1 = 1 + 5 2 \lambda_1 = \frac{1 + \sqrt{5}}{2} λ1=21+5 (黄金分割比), λ 2 = 1 − 5 2 \lambda_2 = \frac{1 - \sqrt{5}}{2} λ2=21−5 。
-
求特征向量:
- 对 λ 1 = 1 + 5 2 \lambda_1 = \frac{1 + \sqrt{5}}{2} λ1=21+5 ,解 ( A − λ 1 I ) v ⃗ = 0 (A - \lambda_1 I)\vec{v} = 0 (A−λ1I)v =0 ,得特征向量 v 1 ⃗ = [ 1 λ 1 ] \vec{v_1} = \begin{bmatrix} 1 \\ \lambda_1 \end{bmatrix} v1 =[1λ1] ;
- 对 λ 2 = 1 − 5 2 \lambda_2 = \frac{1 - \sqrt{5}}{2} λ2=21−5 ,解 ( A − λ 2 I ) v ⃗ = 0 (A - \lambda_2 I)\vec{v} = 0 (A−λ2I)v =0 ,得特征向量 v 2 ⃗ = [ 1 λ 2 ] \vec{v_2} = \begin{bmatrix} 1 \\ \lambda_2 \end{bmatrix} v2 =[1λ2] 。
-
构建对角化矩阵 :
特征基变换矩阵 P = [ 1 1 λ 1 λ 2 ] P = \begin{bmatrix} 1 & 1 \\ \lambda_1 & \lambda_2 \end{bmatrix} P=[1λ11λ2] ,其逆矩阵为
P − 1 = 1 λ 2 − λ 1 [ λ 2 − 1 − λ 1 1 ] P^{-1} = \frac{1}{\lambda_2 - \lambda_1} \begin{bmatrix} \lambda_2 & -1 \\ -\lambda_1 & 1 \end{bmatrix} P−1=λ2−λ11[λ2−λ1−11]对角矩阵 Λ = [ λ 1 0 0 λ 2 ] \Lambda = \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} Λ=[λ100λ2] ,则 A = P Λ P − 1 A = P\Lambda P^{-1} A=PΛP−1 。
-
计算 A n A^n An 并导出通项公式 :
由对角化性质, A n = P Λ n P − 1 A^n = P\Lambda^n P^{-1} An=PΛnP−1 ,其中 Λ n = [ λ 1 n 0 0 λ 2 n ] \Lambda^n = \begin{bmatrix} \lambda_1^n & 0 \\ 0 & \lambda_2^n \end{bmatrix} Λn=[λ1n00λ2n] 。代入矩阵乘法展开后,结合 A n = [ F n − 1 F n F n F n + 1 ] A^n = \begin{bmatrix} F_{n-1} & F_n \\ F_n & F_{n+1} \end{bmatrix} An=[Fn−1FnFnFn+1] 的(2,1)位置元素,可得:
F n = 1 5 [ ( 1 + 5 2 ) n − ( 1 − 5 2 ) n ] F_n = \frac{1}{\sqrt{5}} \left[ \left( \frac{1 + \sqrt{5}}{2} \right)^n - \left( \frac{1 - \sqrt{5}}{2} \right)^n \right] Fn=5 1[(21+5 )n−(21−5 )n]此即为斐波那契数列的通项公式(比内公式)。
11 抽象向量空间
向量的广义定义
向量并非局限于"箭头"或"有序数列表",满足特定运算规则的任意对象均可视为向量(如函数、多项式等)。
函数作为向量的示例
- 向量加法: ( f + g ) ( x ) = f ( x ) + g ( x ) (f + g)(x) = f(x) + g(x) (f+g)(x)=f(x)+g(x)(对应数列表的分量相加)。
- 向量数乘: ( c f ) ( x ) = c f ( x ) (cf)(x) = cf(x) (cf)(x)=cf(x)(对应数列表的分量数乘)。
- 多项式的向量表示:多项式 a n x n + ⋯ + a 1 x + a 0 a_nx^n + \cdots + a_1x + a_0 anxn+⋯+a1x+a0 可表示为无穷维向量 [ a 0 a 1 ⋮ a n 0 ⋮ ] \begin{bmatrix} a_0\\ a_1\\ \vdots\\ a_n\\ 0\\ \vdots \end{bmatrix} a0a1⋮an0⋮ ,基函数为 { 1 , x , x 2 , x 3 , ... } \{1,x,x^2,x^3,\ldots\} {1,x,x2,x3,...}。
线性变换的广义形式
- 函数的线性变换(称为线性算子 ):接收一个函数并输出另一个函数,需满足线性性质 L ( f + g ) = L ( f ) + L ( g ) L(f + g) = L(f) + L(g) L(f+g)=L(f)+L(g) 且 L ( c f ) = c L ( f ) L(cf) = cL(f) L(cf)=cL(f)。
- 示例:求导算子 d d x \frac{d}{dx} dxd 是线性算子,因 ( f + g ) ′ = f ′ + g ′ (f + g)' = f' + g' (f+g)′=f′+g′ 且 ( c f ) ′ = c f ′ (cf)' = cf' (cf)′=cf′。
- 线性算子的矩阵表示:以多项式空间为例,求导算子在基 { 1 , x , x 2 , x 3 , ... } \{1,x,x^2,x^3,\ldots\} {1,x,x2,x3,...} 下的矩阵为:
d d x ↔ [ 0 1 0 0 ⋯ 0 0 2 0 ⋯ 0 0 0 3 ⋯ ⋮ ⋮ ⋮ ⋮ ⋱ ] \frac{d}{dx} \leftrightarrow \begin{bmatrix} 0&1&0&0&\cdots\\ 0&0&2&0&\cdots\\ 0&0&0&3&\cdots\\ \vdots&\vdots&\vdots&\vdots&\ddots \end{bmatrix} dxd↔ 000⋮100⋮020⋮003⋮⋯⋯⋯⋱
例: d d x ( x 3 + 5 x 2 + 4 x + 5 ) = 3 x 2 + 10 x + 4 \frac{d}{dx}(x^3 + 5x^2 + 4x + 5) = 3x^2 + 10x + 4 dxd(x3+5x2+4x+5)=3x2+10x+4,对应矩阵与向量的乘积:0 1 0 0 ⋯ 0 0 2 0 ⋯ 0 0 0 3 ⋯ ⋮ ⋮ ⋮ ⋮ ⋱ \] \[ 5 4 5 1 ⋮ \] = \[ 4 10 3 0 ⋮ \] \\begin{bmatrix} 0\&1\&0\&0\&\\cdots\\\\ 0\&0\&2\&0\&\\cdots\\\\ 0\&0\&0\&3\&\\cdots\\\\ \\vdots\&\\vdots\&\\vdots\&\\vdots\&\\ddots \\end{bmatrix} \\begin{bmatrix} 5\\\\ 4\\\\ 5\\\\ 1\\\\ \\vdots \\end{bmatrix} = \\begin{bmatrix} 4\\\\ 10\\\\ 3\\\\ 0\\\\ \\vdots \\end{bmatrix} 000⋮100⋮020⋮003⋮⋯⋯⋯⋱ 5451⋮ = 41030⋮
一个集合若要被称为向量空间,其元素(向量)的加法和数乘运算需满足以下八条公理:
- u ⃗ + ( v ⃗ + w ⃗ ) = ( u ⃗ + v ⃗ ) + w ⃗ \vec{u} + (\vec{v} + \vec{w}) = (\vec{u} + \vec{v}) + \vec{w} u +(v +w )=(u +v )+w (加法结合律)。
- v ⃗ + w ⃗ = w ⃗ + v ⃗ \vec{v} + \vec{w} = \vec{w} + \vec{v} v +w =w +v (加法交换律)。
- 存在零向量 0 ⃗ \vec{0} 0 ,使得 0 ⃗ + v ⃗ = v ⃗ \vec{0} + \vec{v} = \vec{v} 0 +v =v (零元存在)。
- 对任意向量 v ⃗ \vec{v} v ,存在负向量 − v ⃗ -\vec{v} −v ,使得 v ⃗ + ( − v ⃗ ) = 0 ⃗ \vec{v} + (-\vec{v}) = \vec{0} v +(−v )=0 (负元存在)。
- a ( b v ⃗ ) = ( a b ) v ⃗ a(b\vec{v}) = (ab)\vec{v} a(bv )=(ab)v (数乘结合律)。
- 1 ⋅ v ⃗ = v ⃗ 1 \cdot \vec{v} = \vec{v} 1⋅v =v (数乘单位元)。
- a ( v ⃗ + w ⃗ ) = a v ⃗ + a w ⃗ a(\vec{v} + \vec{w}) = a\vec{v} + a\vec{w} a(v +w )=av +aw (数乘分配律1)。
- ( a + b ) v ⃗ = a v ⃗ + b v ⃗ (a + b)\vec{v} = a\vec{v} + b\vec{v} (a+b)v =av +bv (数乘分配律2)。
"普适的代价是抽象"(Abstractness is the price of generality.)
对应关系
| 线性代数中的概念 | 应用于函数空间时的别名 |
|---|---|
| 线性变换 | 线性算子 |
| 点积 | 内积 |
| 特征向量 | 特征函数 |
12 克莱姆法则,几何解释
正交变换的性质
- 定义:若线性变换 T T T 满足对任意向量 v ⃗ , w ⃗ \vec{v},\vec{w} v ,w ,有 T ( v ⃗ ) ⋅ T ( w ⃗ ) = v ⃗ ⋅ w ⃗ T(\vec{v}) \cdot T(\vec{w}) = \vec{v} \cdot \vec{w} T(v )⋅T(w )=v ⋅w ,则称 T T T 为正交变换。
- 几何意义:正交变换保持向量的长度和夹角不变(基向量保持单位长度且相互垂直)。
克莱姆法则的几何本质
克莱姆法则用于求解线性方程组 A x ⃗ = b ⃗ A\vec{x} = \vec{b} Ax =b ,即利用行列式的面积(体积)缩放性质。
二维情形推导
设 A = [ a b c d ] A = \begin{bmatrix} a&b\\ c&d \end{bmatrix} A=[acbd], x ⃗ = [ x y ] \vec{x} = \begin{bmatrix} x\\ y \end{bmatrix} x =[xy], b ⃗ = [ e f ] \vec{b} = \begin{bmatrix} e\\ f \end{bmatrix} b =[ef],方程组等价于 x [ a c ] + y [ b d ] = [ e f ] x\begin{bmatrix} a\\ c \end{bmatrix} + y\begin{bmatrix} b\\ d \end{bmatrix} = \begin{bmatrix} e\\ f \end{bmatrix} x[ac]+y[bd]=[ef]。
- 几何意义: b ⃗ \vec{b} b 是 A A A 的列向量的线性组合,系数为 x , y x,y x,y。
- 面积关系:
- 列向量 [ a c ] \begin{bmatrix} a\\ c \end{bmatrix} [ac] 与 [ e f ] \begin{bmatrix} e\\ f \end{bmatrix} [ef] 张成的平行四边形面积为 det ( [ a e c f ] ) \det\left( \begin{bmatrix} a&e\\ c&f \end{bmatrix} \right) det([acef])。
- 该面积等于 y × det ( A ) y \times \det(A) y×det(A)(因 y y y 是 [ b d ] \begin{bmatrix} b\\ d \end{bmatrix} [bd] 的缩放比例,面积缩放比例为 y y y)。
- 解的表达式: y = det ( [ a e c f ] ) det ( A ) y = \frac{\det\left( \begin{bmatrix} a&e\\ c&f \end{bmatrix} \right)}{\det(A)} y=det(A)det([acef]),同理 x = det ( [ e b f d ] ) det ( A ) x = \frac{\det\left( \begin{bmatrix} e&b\\ f&d \end{bmatrix} \right)}{\det(A)} x=det(A)det([efbd])。
高维推广
三维及更高维度中,解的分量可表示为"替换列向量后的行列式"与"系数矩阵行列式"的比值,本质是体积缩放比例的逆用。
13 计算二阶矩阵特征值的妙计
矩阵的迹与行列式的性质
对于二阶矩阵 A = [ a b c d ] A = \begin{bmatrix} a&b\\ c&d \end{bmatrix} A=[acbd]:
- 迹(Trace) : t r ( A ) = a + d {\rm tr}(A) = a + d tr(A)=a+d,且满足 t r ( A ) = λ 1 + λ 2 {\rm tr}(A) = \lambda_1 + \lambda_2 tr(A)=λ1+λ2(特征值之和等于矩阵的迹)。
- 行列式 : det ( A ) = a d − b c \det(A) = ad - bc det(A)=ad−bc,且满足 det ( A ) = λ 1 λ 2 \det(A) = \lambda_1 \lambda_2 det(A)=λ1λ2(特征值之积等于矩阵的行列式)。
特征值的快速计算
- 设特征值的平均值为 m = λ 1 + λ 2 2 = t r ( A ) 2 m = \frac{\lambda_1 + \lambda_2}{2} = \frac{{\rm tr}(A)}{2} m=2λ1+λ2=2tr(A)。
- 设特征值的乘积为 p = λ 1 λ 2 = det ( A ) p = \lambda_1 \lambda_2 = \det(A) p=λ1λ2=det(A)。
- 由一元二次方程根与系数的关系,特征值满足方程 t 2 − 2 m t + p = 0 t^2 - 2mt + p = 0 t2−2mt+p=0,解得:
λ 1 , 2 = m ± m 2 − p = t r ( A ) 2 ± ( t r ( A ) 2 ) 2 − det ( A ) \lambda_{1,2} = m \pm \sqrt{m^2 - p} = \frac{{\rm tr}(A)}{2} \pm \sqrt{\left( \frac{{\rm tr}(A)}{2} \right)^2 - \det(A)} λ1,2=m±m2−p =2tr(A)±(2tr(A))2−det(A)
例:矩阵 A = [ 3 1 1 2 ] A = \begin{bmatrix} 3&1\\ 1&2 \end{bmatrix} A=[3112], t r ( A ) = 3 + 2 = 5 {\rm tr}(A) = 3 + 2 = 5 tr(A)=3+2=5, det ( A ) = 3 × 2 − 1 × 1 = 5 \det(A) = 3×2 - 1×1 = 5 det(A)=3×2−1×1=5,则:
m = 5 2 m = \frac{5}{2} m=25,
m 2 − p = ( 5 2 ) 2 − 5 = 25 4 − 5 = 5 4 m^2 - p = \left( \frac{5}{2} \right)^2 - 5 = \frac{25}{4} - 5 = \frac{5}{4} m2−p=(25)2−5=425−5=45,
λ 1 , 2 = 5 2 ± 5 2 \lambda_{1,2} = \frac{5}{2} \pm \frac{\sqrt{5}}{2} λ1,2=25±25 。
via:
- 分享下本科你读过的写的最好的一本数学书? - 知乎
https://www.zhihu.com/question/306215466 - 3Blue1Brown线性代数笔记:可能是全网最好的中英文整理
https://mp.weixin.qq.com/s/UcdvTSsjKawoT7TbzbwehQ - 【笔记】3Blue1Brown线性代数的本质 - 知乎
https://zhuanlan.zhihu.com/p/457858293