【c++知识铺子】相对简单的容器适配器双生子-stack和queue（STL）

爱装代码的小瓶子2025-11-18 10:16

关注我，学习c++不迷路:

个人主页：爱装代码的小瓶子

专栏如下：

  1. c++学习
  2. Linux学习

后续会更新更多有趣的小知识，关注我带你遨游知识世界

期待你的关注。

文章目录

  • [1. stack和queue的简单介绍：](#1. stack和queue的简单介绍：)
  • [2. stack和queue实现](#2. stack和queue实现)
    • [2.1 容器适配器](#2.1 容器适配器)
    • [2.2 了解deque：](#2.2 了解deque：)
    • [2.3 stack的实现：](#2.3 stack的实现：)
    • [2.4 queue的实现：](#2.4 queue的实现：)
  • 3.堆（优先级队列）
  • [4. 总结：](#4. 总结：)

1. stack和queue的简单介绍：

stack就是栈我们在C语言专栏里面已经讲过了，这里我们简单回顾一下，他是先进后出，类似与我家乡老式的月饼，先进去压在了最底下，后进去的在上面，要吃也只能吃最上面的，它满足后进先出 (LIFO)。同时他也操作受限：所有操作都只能在栈顶进行，无法直接访问栈中间的元素。

queue就是队列，它满足先进先出，就像奶茶点门口的队伍一样，，先在队伍里面的先拿到奶茶。但是在cpp中queue这个头文件还包括多种容器。

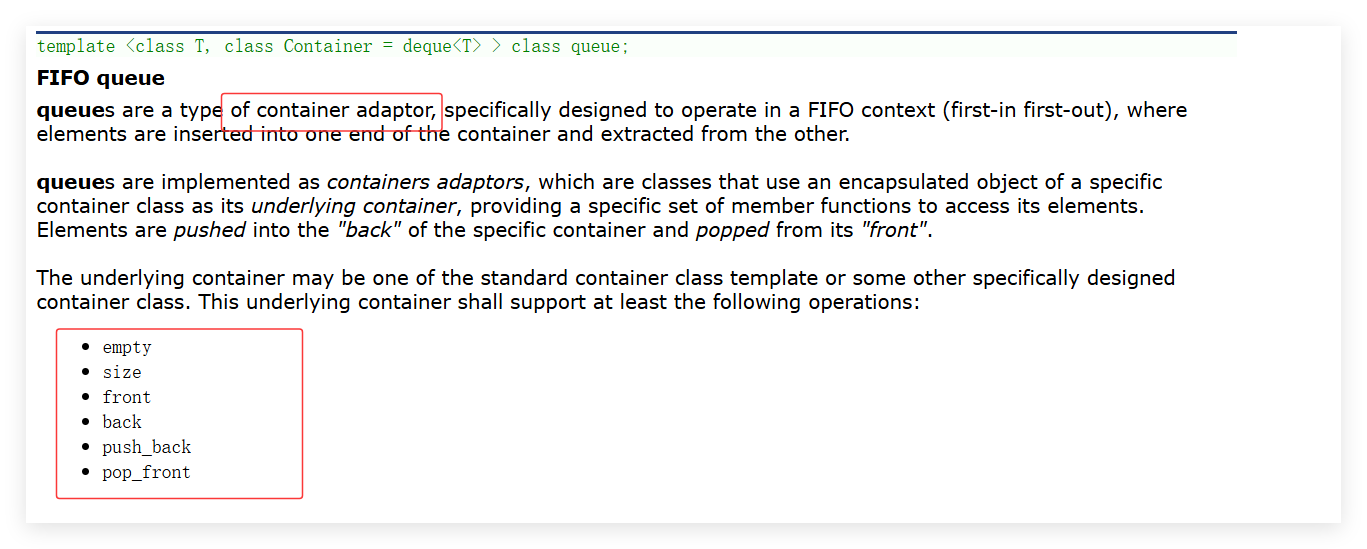
两个接口也都比较少。相比与之前的vector和list，这两个接口都算比较小的。他们的特性都很特别。

2. stack和queue实现

2.1 容器适配器

在讲stack的实现之前，我们需要讲明白什么是容器适配器，按我的理解就是用别的容器封装过后完成对本容器的实现。你可以将它想象成一个接口转换器，就像电源适配器能把墙上的交流电转换成电器所需的直流电一样，容器适配器将底层容器提供的通用接口"转换"成栈、队列等特定数据结构的专用接口。

他主要的思想是：容器适配器的核心模式是"封装"与"复用"。

它不自己管理数据存储，而是内置一个底层容器对象，将所有对适配器的操作请求转发给这个内部容器，但只暴露符合目标数据结构规则的有限接口。这也符合cpp的三大特性之一：封装。我们无需关注底层的实现，调用时只需关注接口。当然如果你也需要了解。

2.2 了解deque：

我们观察stack和queue中发现：他的默认都是使用deque来完成实现的，那么什么时deque：deque是 Double Ended Queue（双端队列）的缩写。你可以将它理解为一个可以在头部和尾部都能快速进行插入和删除操作的线性集合。

它的核心特性在于双端操作，这使其既可以像栈（Stack）一样作为后进先出（LIFO）​ 的结构使用，也可以像普通队列（Queue）一样作为先进先出（FIFO）​ 的结构使用，非常灵活。

其实deque是介于vector和list的一种容器，他打算结合list和vector的优点，但其实他也有缺点，不然他就早就代替了list和vector。

那么他是怎么做到的呢？

组件名称 核心功能 类比理解
**中控器 (Map)**​ 一个指针数组，每个指针指向一块缓冲区，负责管理所有缓冲区。 像一本书的目录，记录着每个章节（缓冲区）的起始页码。
**缓冲区 (Buffer)**​ 实际存储元素的定长连续内存块。 书中的每一个章节，其内部内容是连续的。
**迭代器 (Iterator)**​ 包含多个指针，用于在分段缓冲区上导航，维持"逻辑连续"的假象。 一个功能强大的书签，不仅能定位句子，还能在章节间跳转。

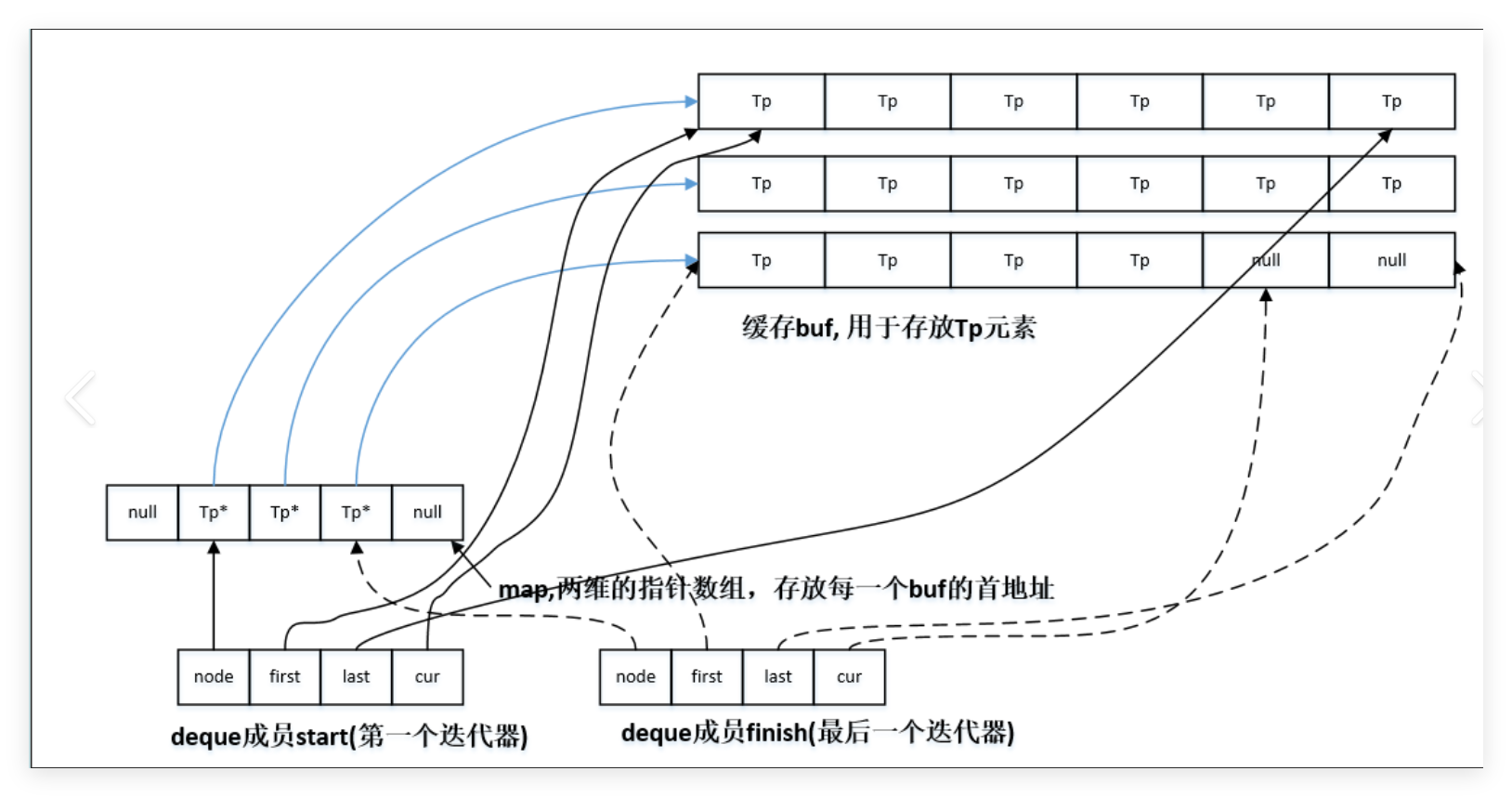
这样这样的结构中既包含了vector和list。

  1. 我们先来讲讲中控器：控器本身是一块小的连续空间（通常是一个指针数组或向量），它并不存储实际数据，而是存储指向各个缓冲区的指针。这种设计使得Deque在需要增加新的缓冲区时，主要调整的是中控器，而不需要大规模移动实际数据。如果中控器不够用，我们可以像vector底层一样，先new出新的数组，再将里面的内容拷贝进去。这样就避免了vector扩容时的浪费。同时中控器一般现在中间放置指针。这样有利于后续的两端删除和头插。
  2. 缓冲区 (Buffer)：缓冲区是真正的数据仓库。每个缓冲区的大小通常是固定的（例如，默认可能基于512字节和元素大小计算得出），这避免了像vector那样一次性扩容需要迁移全部数据的开销。这就时数组的特性，地址时连续的，避免了list在内存上的空间时离散的。我们buff的地址已经存在了中控器中了。
  3. 迭代器 (Iterator)：Deque的迭代器比vector的简单指针复杂得多，它通常包含四个关键指针：
    • cur：指向当前迭代器正在访问的元素。
    • first：指向当前所在缓冲区的起始位置。
    • last：指向当前所在缓冲区的结束位置。
    • node：一个指向中控器的指针，用于定位当前缓冲区在Map中的位置。

当迭代器++或--操作到达当前缓冲区的边界时，它会通过node找到下一个或上一个缓冲区，并更新first、last和cur，从而实现跨缓冲区的无缝遍历。

这个迭代器也不是我们之前所讲的的普通的指针了。

基于上述结构，Deque的高效操作就很好理解了：

  • 双端插入/删除 (push_back, push_front, pop_back, pop_front)：这些操作通常可以在常数时间O(1)内完成。原理是直接在当前头部或尾部的缓冲区中进行操作。如果当前缓冲区已满，只需分配一个新的缓冲区，并在中控器中添加或调整相应指针即可，无需移动大量现有元素。
  • 随机访问 (operator[]) ：Deque可以通过下标在O(1)时间内访问元素。它通过一个简单的计算来定位目标元素：元素位置 = 下标索引 / 每个缓冲区可容纳的元素数量，从而找到对应的缓冲区；块内偏移 = 下标索引 % 每个缓冲区可容纳的元素数量，从而在缓冲区内定位。
  • 扩容机制 ：Deque的扩容主要发生在两个方面：
    1. 缓冲区不足：当一端需要插入元素但没有空间时，会分配一个新的缓冲区，并链接到中控器的首部或尾部。
    2. 中控器不足：当中控器（Map）的空间不够存放更多的缓冲区指针时，会重新分配一个更大的中控器，并将原有的指针复制过去。这个过程相对耗时，但发生的频率很低。

我们已经看到了优点，那么缺点呢：

我们发现，他的内部在进行下标访问时完全不如vector，也就时在排序算法中，他是完全比不够vector的。这是因为他的内部进行大量的计算，同时在指定位置进行插入或者删除也是很麻烦的。需要大量的挪动数据，这是及其麻烦的一个动作。

因此，Deque非常适合以下场景：

  • 需要频繁在序列头部和尾部进行添加或删除操作。一个典型的例子是作为标准库中std::stack和std::queue的默认底层容器。
  • 需要随机访问，但对绝对极致的访问速度要求不是最高，且可能涉及头部操作，使用vector会导致头部操作成为性能瓶颈的情况。

我们再来观察stack和queue，我们发现deque简直就时天生适配啊，他们几乎只暴露了头部或者尾部的接口。

2.3 stack的实现：

上面讲了那么多，我们开始尝试实现：

cpp 复制代码 
#include<iostream>
#include<deque>

namespace wwh {

	template <class T,class con = std::deque<T>>
	class stack {
	public:
		stack()
		{
		};//里面什么也不写，也会调用deque的构造，来完成构造。

		~stack()
		{
		};

		void push(const T& val)
		{
			//调用内部适配器的功能满足这个接口。
			_con.push_back(val);
		}

		void pop()
		{
			//栈只能先删除最上面的即最后面的
			_con.pop_back();
		}

		bool empty()
		{
			return _con.empty();//return 不能忘记。
		}

		size_t size()
		{
			return _con.size();
		}

		const T& top()const
		{
			return _con.back();
		}

	private:
		con _con;
	};
}

测试结果如下：

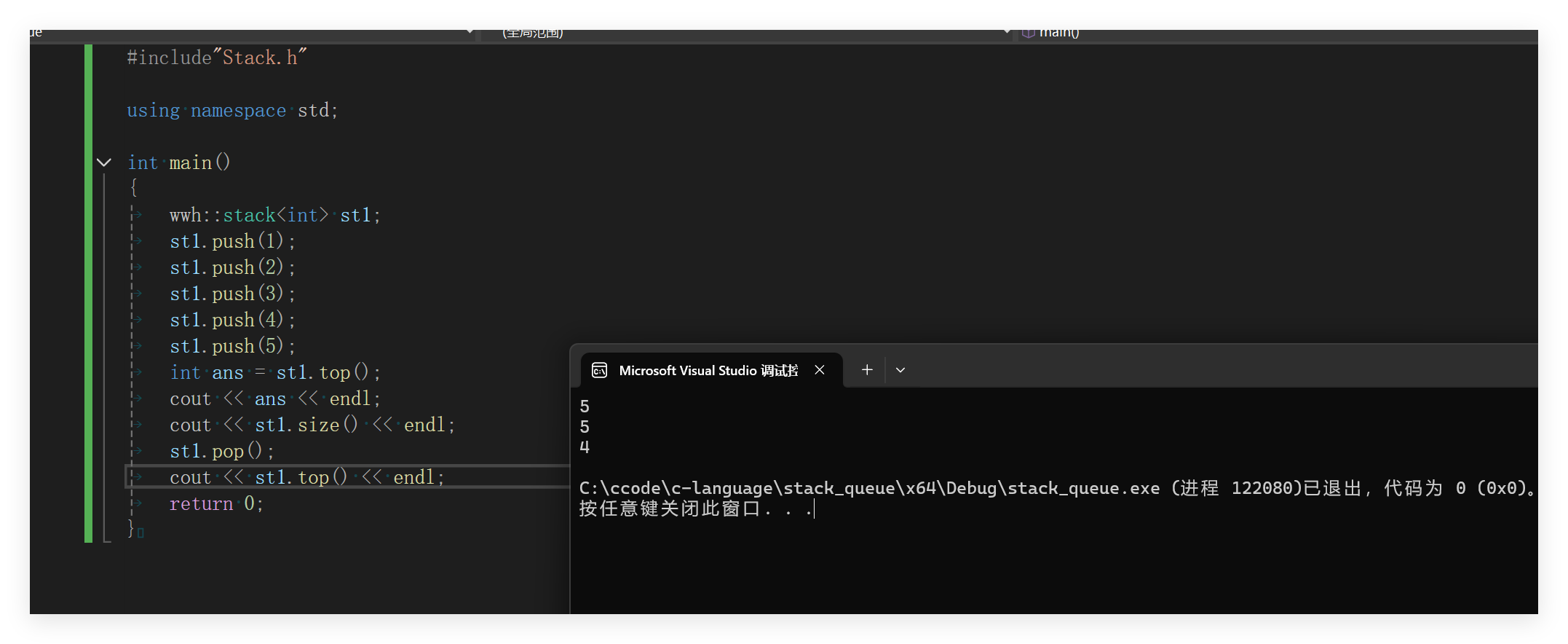
此时的实现还是比较简单的。只需要简单利用已经实现的库接口就行了，这也是体现了cpp中封装的思想。

2.4 queue的实现：

这个和上面的stack是一样的，实现起来也很简单：

cpp 复制代码 
#pragma once
#include<deque>

namespace wwh {
	template  <class T, class Cons = std::deque<T>>
	class queue {
	public:
		queue()
		{
		};

		~queue()
		{
		};

		bool empty()const
		{
			return _con.empty();
		}

		size_t size()const
		{
			return _con.size();
		}

		void push(const T& val)
		{
			_con.push_back(val);
		}

		void pop()
		{
			_con.pop_front();
		}

		const T& back()const
		{
			return _con.back();
		}

		const T& front()const
		{
			return _con.front();
		}
		
	private:
		Cons _con;
	};
}

测试结果如下：

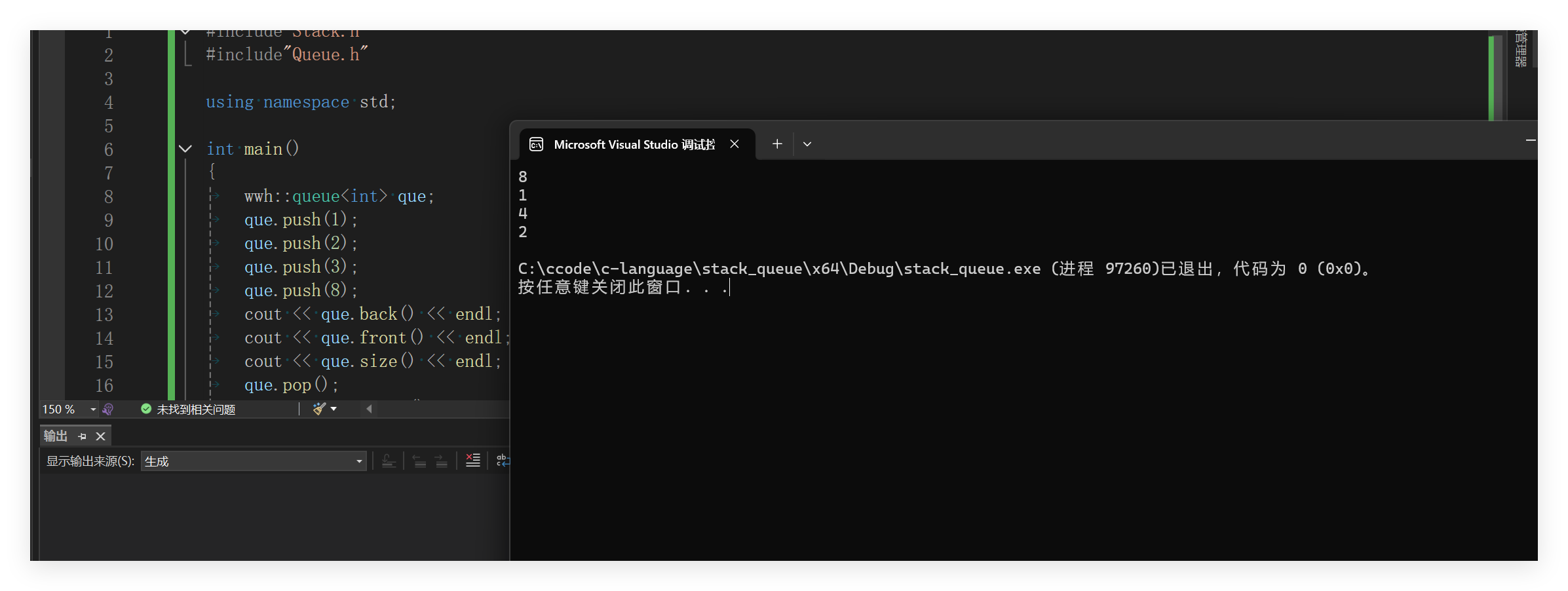
目前看来还是比较容易的。

3.堆（优先级队列）

3.1 什么是priority_queue?

在数据结构中我们把这种父亲大于两孩子的二叉树叫做堆（heap），但是在STL容器中我们叫做优先级队列（priority_queue）,这种容器方便我们找寻最大或者最小数。同理这里的方式和我们在数据结构讲的一样，也是利用向下或者向上建堆方法来完成。

优先级队列的规律：

  • 左子节点 = 2*i + 1；
  • 右子节点 = 2*i + 2；
  • 那么倒退回去，我们就有：父亲节点为：某个子节点的索引为 i，则其父节点的索引为 (i - 1) / 2。

在回顾一下，什么是大堆，什么是小堆？

  • 大堆： 大堆就是父亲大于孩子节点。
  • 小堆：小堆就是父亲小于孩子节点。

两个方法：

向下建堆方法和向下建堆方法：

我们在数据结构那边初步解释了：我们一开始是使用向上建堆方式来完成构建大小堆的，但是向上建堆这种方式时间复杂度高，最后一层几乎占据了50%。但是这种方式我们最先理解的。向下建堆的方式有一种分治的思想：即每次每次从最后一个的父亲节点开始完成调整。

两种建堆方式的比较：

特性维度 向上调整建堆 (AdjustUp) 向下调整建堆 (AdjustDown)
调整方向​ 自底向上：从子节点向根节点调整 自顶向下：从根节点向子节点调整
起始点​ 从数组第二个元素开始（索引1），模拟依次插入 从最后一个非叶子节点 开始（索引 (n-2)/2）
时间复杂度​ O(N logN) O(N)
前提条件​ 待调整节点之前的所有元素必须已经构成一个堆 待调整节点的左右子树都必须已经是堆
典型应用​ 适用于数据逐个插入的动态建堆场景 适用于直接对已有完整数组进行高效建堆

3.2 什么是仿函数：

本质上来讲，其实仿函数本质不是函数，而是一个类或者类的对象。

我们在使用priority_queue中会经常用到它，这是我们需要通过他来完成控制是建立小堆还是大堆。我们先看他的作用吧：

cpp 复制代码 
#include <iostream>
// 一个简单的加法仿函数
class MyAdder {
public:
    // 重载函数调用运算符 ()
    int operator()(int a, int b) const {
        return a + b;
    }
};

int main() {
    MyAdder adder; // 创建仿函数对象
    int result = adder(10, 20); // 像函数一样调用：result = 30
    std::cout << "10 + 20 = " << result << std::endl;
    return 0;
}

有了这个初步想法，我们可以定义一个less类和greater类，里面分别return a < b 和 return a > b;这样我们就能控制什么时候建立大堆和小堆。

在C++模板编程中，模板参数通常需要是一个类型，而不是一个函数指针。仿函数是类，其类型自然可以作为模板参数传递。这使得STL中的算法（如sort, find_if）非常灵活，你可以轻松地传入自定义的比较或计算规则。

cpp 复制代码 
#include <algorithm>
#include <vector>
// 自定义一个比较规则（按绝对值大小排序）
struct AbsoluteCompare {
    bool operator()(int a, int b) const {
        return std::abs(a) < std::abs(b);
    }
};

int main() {
    std::vector<int> vec = {-5, 2, -8, 1};
    // 将仿函数类型 AbsoluteCompare 的实例传递给 sort 算法
    std::sort(vec.begin(), vec.end(), AbsoluteCompare());
    // 现在 vec 为: {1, 2, -5, -8}
    return 0;
}

3.3priority_queue的简单实现：

有了上面的前置的知识，我们就可以实现优先级队列了，那么我们来尝试一下吧：

cpp 复制代码 
#pragma once
#include<functional>
#include<vector>

namespace wwh {
	template<class T, class Cons = std::vector<T>,class compare = std:: less<T>>
	class priority_queue {
	public:
		bool empty()const
		{
			return _con.empty();
		}
	
		size_t size()const
		{
			return _con.size();
		}

		const T& top()const
		{
			return _con.front();
		}

		void ad_justUp(size_t child)
		{
			size_t parent = (child - 1) / 2;
			while (child > 0)
			{
				if(_com(_con[parent],_con[child]))
				{
					//_con[parent] < _con[child],大的上去，默认是大堆
					std::swap(_con[parent], _con[child]);
					//开始更新下标,开始向上调整。
					child = parent;
					parent = (child - 1) / 2;
				}
				else {
					//如果没有这个将进入死循环。
					break;
				}
			}
		}

		void ad_justDown(size_t parent)
		{
			size_t sz = _con.size(); 
			size_t child = parent * 2 + 1;
 			while (child < sz)
			{
				if (child + 1 < sz &&_com(_con[child], _con[child + 1]))
				{
					child = child + 1;
				}
				if (_com(_con[parent], _con[child]))
				{
					std::swap(_con[parent], _con[child]);
					parent = child;
					child = parent * 2 + 1;
				}
				else {
					//已经满足堆的条件，直接结束。
					break;
				}

			}
		}


		void push(const T& val)
		{
			//在这个函数中，插入应该使用向上调整建堆
			_con.push_back(val);
			ad_justUp(_con.size() - 1);
		}

		void pop()
		{
			if (_con.empty())
				return;
			std::swap(_con[0], _con[_con.size() - 1]);
			_con.pop_back();
			if(!_con.empty())
				ad_justDown(0);
		}

	private:
		Cons _con;
		compare _com;//仿函数，里面重载了();其本质是一个类。
	};


}

在最开始，我们在实现时发现向下和向上调整算法，里面传入什么变量名比较好，这里正好做个总结：

  • 如果是 向下调整算法，那么就应该传入父亲节点。
  • 如果是 向上调整算法，那么就应该传入孩子节点。

测试结果如下：

4. 总结：

这期我们主要讲了stack和queue，在queue中我们就又讲了什么是deque和priority_queue,这些容器还是很重要的，在很多算法题中都有涉及。

相关推荐
豐儀麟阁贵2 小时前
6.2 Object类
java·开发语言·python
MichaelIp2 小时前
Python同步vs异步性能对比实验-2
开发语言·python·性能优化·可用性测试
white-persist2 小时前
二进制movl及CTF逆向GDB解析：Python（env）环境下dbg从原理到实战
linux·服务器·开发语言·python·网络安全·信息可视化·系统安全
脏脏a2 小时前
类和对象（下）：初始化列表、静态成员与友元深度解析
开发语言·c++
lkbhua莱克瓦242 小时前
Java进阶——集合进阶（MAP）
java·开发语言·笔记·github·学习方法·map
代码狂想家2 小时前
Rust 命令行密码管理器工具开发
开发语言·rust·php
u0119608232 小时前
java 不可变集合讲解
java·开发语言
Dream it possible！2 小时前
LeetCode 面试经典 150_二叉树_二叉树中的最大路径和（77_124_C++_困难）（DFS）
c++·leetcode·面试·二叉树
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03BongoCat - 跨平台键盘猫动画工具04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06Valdi：Snapchat 开源的新一代跨平台 UI 框架07综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件08Labelme从安装到标注：零基础完整指南09jdk21下载、安装（Windows、Linux、macOS）10使用国内镜像网站在线下载安装Qt（解决官网慢的问题）——Qt