一、电压利用率是什么
1.1 电压分析
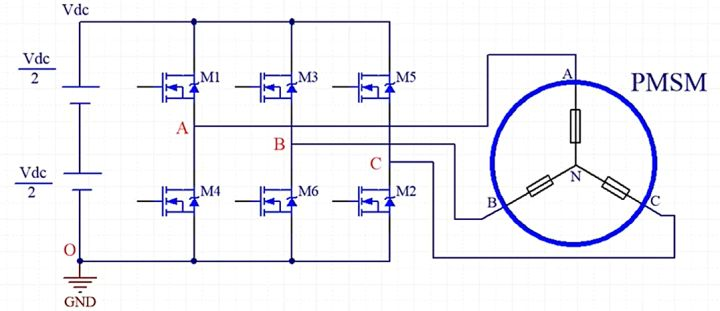
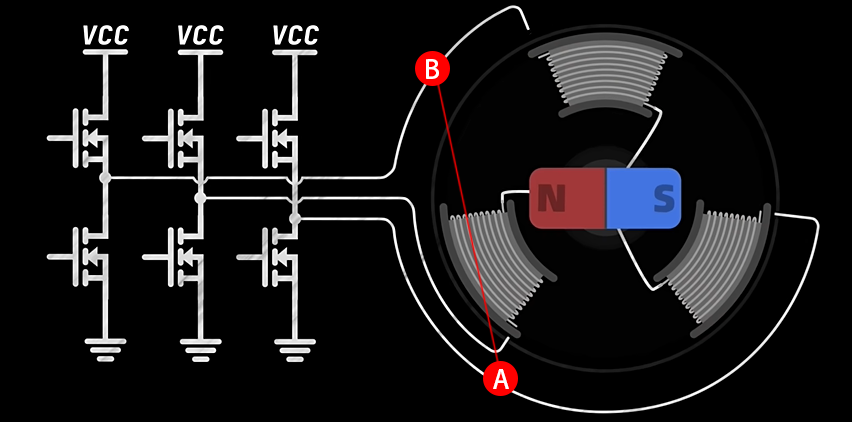
根据上图所示的连接方式,可以分析端电压
- 当控制 M1 的占空比为 100% 时,端电压
- 当控制 M1 的占空比为 50% 时,端电压
- 当控制 M1 的占空比为 0% 时,端电压
1.2 电压利用率是什么
电压利用率 = 逆变器能输出的最大相电压(峰值,非峰峰值) / 母线电压。
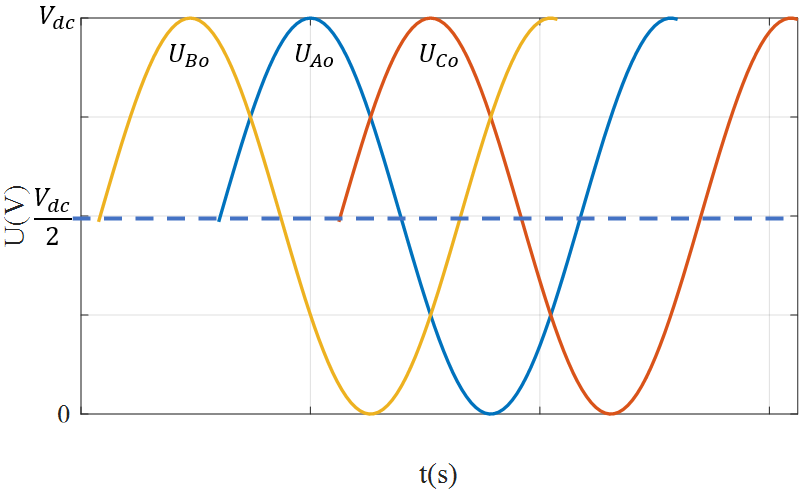
比如下图是我们使用 SVPWM 输出的相电压,其相电压利用率为 50%,我们可见每一项的峰值只有母线电压的一半。
而线电压利用率却是 86.6%,我们继续向下看:
二、相电压和线电压的关系
2.1 相电压和线电压是什么?
三相系统里有三相:A、B、C,每一相的电压如果对地 / 对中性点量,就是相电压。
如下图所示,A 与 B 的点的电压。
线电压是两相之间的电压差。
如下所示,也就是两项之间的电压差,A 点与 B 点。
2.1 相电压和线电压的关系 (向量推导)
虚线是我们将 取负平移后得到的,最终得到
向量,也就是我们是线电压。
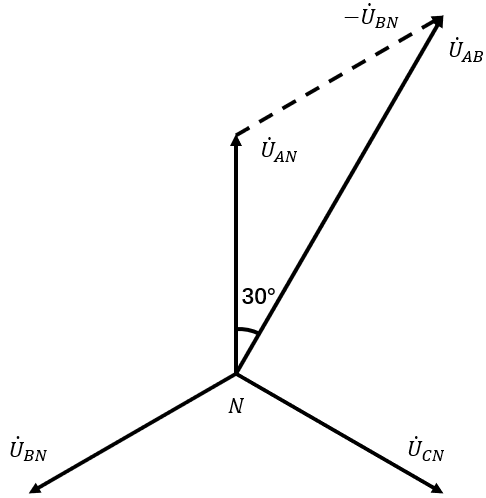
通过构建等腰三角形,可见,
= 线电压
= 相电压
2.2 三角函数公式推导
假设 a、b 两相电压为:
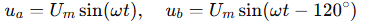
= 电压幅值
线电压就是两者之差:
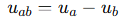
可得:
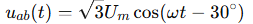
= 电压幅值
忽略交流效应,可得:
= 线电压
= 相电压
2.3 结论
至此,我们可以确定相电压和线电压的关系:
= 线电压
= 相电压
三、SPWM 的电压利用率
2.1 SPWM 的相电压利用率
基于以上分析,三端电压与 的表达式为:
在加下图中,虚线就是我们上面公式最后的 的直流偏置。不难发现,这种调制方式的的峰值为母线电压的一半。

我们这样规定电压利用率:
电压利用率 = 电压幅值 / 直流母线电压。
也就是说,SPWM 的相电压 (三项对地电压) 的电压利用率是 50%。
2.2 SPWM 的线电压利用率
SPWM 的相电压 (三项对地电压) 的电压利用率是 50%,我们刚才发现了相电压和线电压的关系:
= 线电压
= 相电压
所以,SPWM 的线电压利用率就是:
也就是 86.6%
四、SVPWM 电压利用率
4.1 SVPWM 的相电压利用率
我们以零序注入法距离 SVPWM 的电压利用率

、
、
= 三相电的相电压 (线对地电压)
= 相电压峰值
、
、
= 电压120°的超前后滞后
= 零序分量
= 零序分量
= 当前时刻中三项中最大电压
= 当前时刻中三项中最小电压
此时,我们的直流偏置不再是母线电压的一半,而是我们注入的 注入的三角波。
下图中包括了 SPWM、SVPWM 和 SVPWM 注入的三角波偏置的波形。但是并没有显性标识出 SPWM 的偏置电压,很显然就是 0V 直线。
在下图中,SPWM 波形已经到了 0.8V 幅值的母线极限了,但是经过零序分量注入的等量的 SVPWM 后,幅值却低于 SPWM,也就是还有提升的空间,换句话来说,SVPWM 提升了母线电压的利用率。
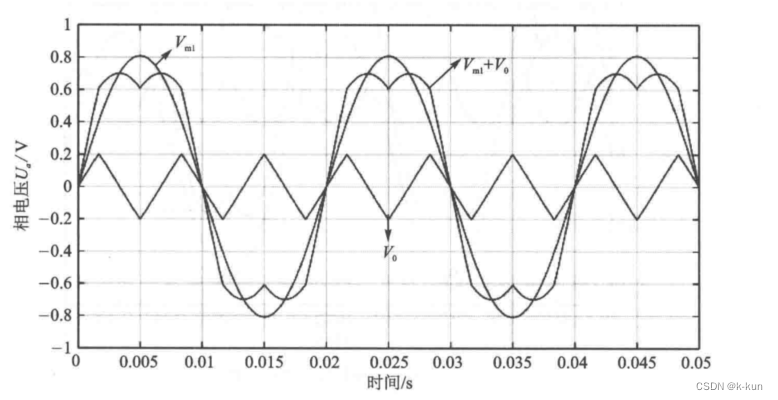
SPWM 的相电压利用率只有 ,但是 SVPWM 处理后则提升到了
。
也就是 SPWM 的的相电压利用率约为 57.73%
2.2 SVPWM 的线电压利用率
我们上述推断可知线电压和相电压关系:
将其带入到我们上述转化可得:
这就是我们使用 SVPWM 的电压利用达到 100% 的推断。
五、总结
|---------------|----------|-----------|
| 测量方式/调制方式 | SPWM | SVPWM |
| 相电压 | 50% | ≈ 57.73% |
| 线电压 | 86.6% | 100% |
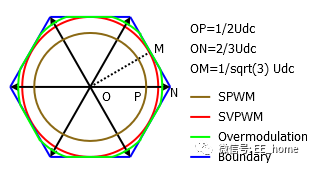
下图是不同调制方式的线电压矢量范围,本文没有涉及到下图绿色和蓝色的过调制。