小红的好矩形

小红的好矩形（牛客网周赛109 E题）

题目描述

小红定义一个两边平行于坐标轴的矩形是"好矩形"，当且仅当其长或宽为 1 1 1。

现给出平面直角坐标系中的 n n n 个互不相同的整点。小红想知道，在其中选四个不同的点作为矩形的顶点，能构成多少个不同的好矩形。

对于两个矩形 A B C D ABCD ABCD、 E F G H EFGH EFGH，称二者不同当且仅当 { A , B , C , D } ≠ { E , F , G , H } \{A,B,C,D\} \neq \{E,F,G,H\} {A,B,C,D}={E,F,G,H}。

输入描述

第一行输入一个整数 n n n（ 1 ≤ n ≤ 2 × 1 0 5 1 \le n \le 2 \times 10^5 1≤n≤2×105）。

之后的 n n n 行，第 i i i 行输入两个整数 x i , y i x_i, y_i xi,yi（ − 1 0 9 ≤ x i , y i ≤ 1 0 9 -10^9 \le x_i, y_i \le 10^9 −109≤xi,yi≤109），代表第 i i i 个点的坐标。

输出描述

输出一个整数，代表能组成好矩形的数量。

示例1

输入

复制代码

输出

复制代码

说明

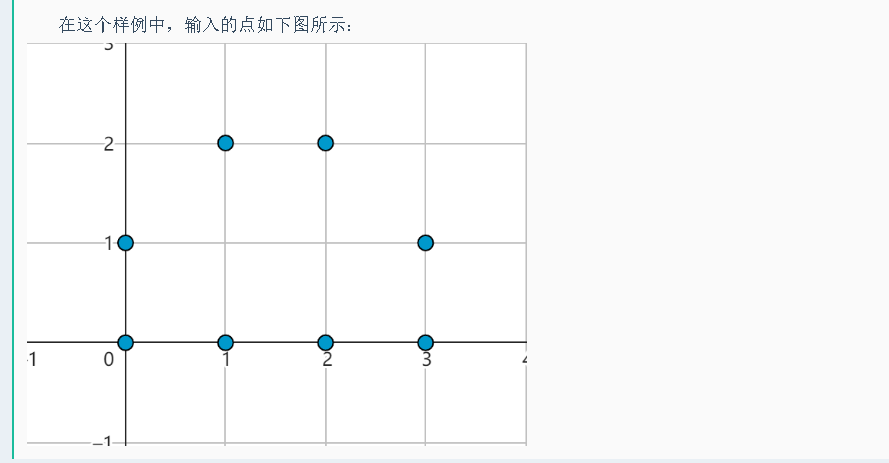
在这个样例中，输入的点如下图所示：

（注：原题配套图示可参考牛客网原题页面，核心构成的两个好矩形分别为：

以 ( 0 , 0 ) 、 ( 0 , 1 ) 、 ( 3 , 0 ) 、 ( 3 , 1 ) (0,0)、(0,1)、(3,0)、(3,1) (0,0)、(0,1)、(3,0)、(3,1) 为顶点的矩形（宽为1）；
以 ( 1 , 2 ) 、 ( 2 , 2 ) 、 ( 1 , 0 ) 、 ( 2 , 0 ) (1,2)、(2,2)、(1,0)、(2,0) (1,2)、(2,2)、(1,0)、(2,0) 为顶点的矩形（长为1））

这个题目只有三种对于矩形的选择只有三种， 1. 1. 1.长为1的矩形 2. {2.} 2. 宽为1的矩形 3. 3. 3.长和宽都为1的矩形。

我们不难想到容斥原理。

那么我们应该如何存呢？对于每个点来说，我们都放到 p a i r < i n t , i n t > pair<int,int> pair<int,int>里，把每个横坐标x的对应的纵坐标y都放到 m a p map map里，把每个纵坐标y的对应的横坐标x放到另一个 m a p map map里。

先找长为1的矩形，我们枚举所有点的横坐标x，枚举当前x对应的所有y坐标，如果存在横坐标为x+1的点，且存在当前枚举的y坐标，那就令cnt1++，我们此时cnt1中的其实是横坐标为x和x+1的共有的y坐标的数量，我们要想组成一个矩形，是不是需要选择两个不同的y坐标？那就是我们需要从cnt1中取出两个y坐标，取出这两个y坐标一定不同。
( c n t 1 2 ) = C ( c n t 1 , 2 ) = c n t 1 × ( c n t 1 − 1 ) 2 \binom{cnt1}{2} = C(cnt1, 2) = \frac{cnt1 \times (cnt1 - 1)}{2} (2cnt1)=C(cnt1,2)=2cnt1×(cnt1−1)

同理，找到宽为1的矩形也是这样，不过我们根据容斥原理我们需要去掉宽为1高为1的矩形，因为我们在计算长为1的矩形中已经算过了。

我们只需要在cnt2++的同时，把在纵坐标为y和纵坐标为y+1的相同的横坐标x存入一个数组里，然后计算所有宽为1的矩形个数 ( c n t 2 2 ) = C ( c n t 2 , 2 ) = c n t 2 × ( c n t 2 − 1 ) 2 \binom{cnt2}{2} = C(cnt2, 2) = \frac{cnt2 \times (cnt2 - 1)}{2} (2cnt2)=C(cnt2,2)=2cnt2×(cnt2−1)，遍历刚刚存储的数组，对于其中的元素（这里用 a [ i ] a[i] a[i]代替）如果存在 a [ i ] + 1 a[i]+1 a[i]+1那就把刚刚计算出来的宽为1的矩形个数减去1，因为这四个点已经构成了一个边长为1的正方形。下面附上代码

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
#define fi first
#define se second
#define ll long long int 
int main(){
    int n;
    cin>>n;
    vector<pii>a;
    for(int i=0;i<n;i++){
    int x,y;
    cin>>x>>y;
    a.push_back({x,y});
    }
    map<int,map<int,int>>xs,ys;
    for(int i=0;i<n;i++){
    int x=a[i].fi,y=a[i].se;
    xs[x][y]=1;
    ys[y][x]=1;
    }
    ll ans=0;
    for(auto i=xs.begin();i!=xs.end();i++){
        int x=i->first;
        auto t=i->second;
        ll cnt=0;
        for(auto j=t.begin();j!=t.end();j++){
            int cury=j->first;
            if(xs.count(x+1)&&xs[x+1].count(cury))cnt++;
        }
        ans+=cnt*(cnt-1)/2;
    }
    
    for(auto i=ys.begin();i!=ys.end();i++){
        int y=i->first;
        auto t=i->second;
       vector<int>memo;
        for(auto j=t.begin();j!=t.end();j++){
            int curx=j->first;
            if(ys.count(y+1)&&ys[y+1].count(curx)){
              memo.push_back(curx);
        }
        }
       ll cnt=memo.size();
        cnt=cnt*(cnt-1)/2;
        for(int i=1;i<memo.size();i++){
            if(memo[i]-memo[i-1]==1)cnt--;
        }
      ans+=cnt;
    }
    cout<<ans;
}

小红的好矩形