栈的介绍和使用

TechNomad2025-11-20 8:13

文章目录

一、栈的基本概念

栈（Stack）是一种后进先出（LIFO, Last In First Out）的线性数据结构。通俗地说：最后放进去的元素最先被取出来，就像一叠盘子，最后放上去的盘子最先拿出来。

栈的主要特点：

栈的基本操作：

二、数组版本的栈实现

cpp 复制代码 
#include <iostream>
using namespace std;

// 顺序栈
class SeqStack {
public:
	SeqStack(int size = 10)
		: mtop(0)
		, mcap(size) {
		mpStack = new int[mcap];
	}

	~SeqStack() {
		delete[] mpStack;
		mpStack = nullptr;
	}

public:
	// 入栈
	void push(int val) {
		if (mtop == mcap) {
			// 栈扩容
			expand(2 * mcap);
		}
		mpStack[mtop++] = val;
	}

	// 出栈
	void pop() {
		if (mtop == 0) {
			throw "stack is empty";
		}
		mtop--; 
	}

	// 获取栈顶元素
	int top() const {
		if (mtop == 0) {
			throw "stack is empty";
		}
		return mpStack[mtop - 1];
	}

	// 栈空
	bool empty() {
		return mtop == 0;
	}

	int size() const {
		return mtop;
	}

private:
	void expand(int size) {
		int* p = new int[size];
		memcpy(p, mpStack, mtop * sizeof(int));
		
		delete[] mpStack;
		mpStack = p;
		mcap = size;
	}

private:
	int* mpStack;
	int mtop; // 栈顶位置
	int mcap; // 栈空间大小
};

int main() {
	int array[] = { 12, 4, 56, 7, 89, 31, 53, 75 };
	
	SeqStack s;
	for (int v : array) {
		s.push(v);
	}

	while (!s.empty()) {
		std::cout << s.top() << " ";
		s.pop();
	}

	return 0;
}

输出结果：

三、链表版的栈实现

cpp 复制代码 
#include <iostream>
using namespace std;

// 链式栈
class LinkStack {
public:
	LinkStack() : size_(0) {
		head_ = new Node;
	}

	~LinkStack() {
		Node* p = head_;
		while (p != nullptr) {
			head_ = head_->next_;
			delete p;
			p = head_;
		}
	}

public:
	// 入栈 O(1) 把链表头节点后面，第一个有笑点的位置，当作栈顶位置
	void push(int val) {
		Node* node = new Node(val);
		node->next_ = head_->next_;
		head_->next_ = node;

		size_++;
	}

	// 出栈 O(1)
	void pop() {
		if (head_->next_ == nullptr) {
			throw "stack is empty!";
		}

		Node* p = head_->next_;
		head_->next_ = p->next_;
		delete p;

		size_--;
	}

	// 获取栈顶操作
	int top() const {
		if (head_->next_ == nullptr) {
			throw "stack is empty!";
		}

		return head_->next_->data_;
	}

	// 判空
	bool empty() const {
		return head_->next_ == nullptr;
	}

	// 返回栈元素个数 O(1)
	int size() const {
		return size_;
	}

private:
	struct Node {
		Node(int data = 0) : data_(data), next_(nullptr) {}

		int data_;
		Node* next_;
	};

	Node* head_;
	int size_;
};

int main() {
	int array[] = { 12, 4, 56, 7, 89, 31, 53, 75 };

	LinkStack s;
	for (int v : array) {
		s.push(v);
	}

	while (!s.empty()) {
		std::cout << s.top() << " ";
		s.pop();
	}

	return 0;
}

输出结果：

四、括号匹配

问题描述：

给定一个只包含括号的字符串，如：

cpp 复制代码 
"([]){}"

要求判断这个字符串的括号是否匹配正确。

匹配规则如下：

  1. 左括号必须用相同类型的右括号闭合；
  2. 左括号必须以正确的顺序闭合；
  3. 每个右括号都有一个对应的相同类型的左括号。

为什么使用栈？

栈是一种后进先出（LIFO） 的数据结构。括号匹配的逻辑恰好与栈的特性吻合：

  • 每当遇到一个左括号 ( [ {，就压入栈；
  • 每当遇到一个右括号 ) ] }，就弹出栈顶元素进行匹配；
  • 如果不匹配或者栈为空，就表示错误；
  • 最后，栈为空则表示匹配完全正确。

算法步骤：

实现代码：

cpp 复制代码 
#include <iostream>
#include <stack>
#include <string>

using namespace std;

bool isMatching(char left, char right) {
	return (left == '(' && right == ')') ||
		(left == '[' && right == ']') ||
		(left == '{' && right == '}');
}

bool isValidParentheses(const string& s) {
	stack<char> st;
	for (char c : s) {
		// 左括号 -> 入栈
		if (c == '(' || c == '[' || c == '{') {
			st.push(c);
		} else if (c == ')' || c == ']' || c == '}') {
			// 右括号 -> 检查匹配
			if (st.empty()) return false; // 没有可匹配的左括号
			
			char top = st.top();
			st.pop();

			if (!isMatching(top, c)) return false; // 类型不匹配

		}
	}

	// 最后栈应为空
	return st.empty();
}

int main() {
	string test1 = "{[()]}";
	string test2 = "([)]";
	string test3 = "((()))";
	string test4 = "{[()]}[";

	cout << test1 << " -> " << (isValidParentheses(test1) ? "匹配正确" : "匹配错误") << endl;
	cout << test2 << " -> " << (isValidParentheses(test2) ? "匹配正确" : "匹配错误") << endl;
	cout << test3 << " -> " << (isValidParentheses(test3) ? "匹配正确" : "匹配错误") << endl;
	cout << test4 << " -> " << (isValidParentheses(test4) ? "匹配正确" : "匹配错误") << endl;
	
	return 0;
}

输出结果：

五、逆波兰表达式（RPN）

逆波兰表达式（Reverse Polish Notation, RPN） 又称为后缀表达式。

它的特点是：

  • 操作符在操作数之后 出现；
  • 不需要括号，计算顺序由表达式本身决定。

例如：

为什么用栈？

逆波兰表达式求值的核心思想是：

  1. 从左到右扫描表达式
  2. 遇到操作数（数字） → 入栈
  3. 遇到运算符 → 从栈中弹出两个操作数，计算结果再入栈
  4. 扫描结束时，栈顶的值就是最终结果

算法步骤

  • 创建一个空栈；
  • 从左到右扫描逆波兰表达式：
  • 如果是数字 → 入栈；
  • 如果是运算符（如 + - * /）：
    • 弹出两个操作数（注意顺序：先弹出的为右操作数 b，后弹出的为左操作数 a）
    • 计算 a op b
    • 将结果压回栈；
  • 扫描结束 → 栈顶元素即为最终结果。

实现示例：

cpp 复制代码 
#include <iostream>
#include <stack>
#include <sstream>
#include <string>
#include <stdexcept>
using namespace std;

// 判断字符串是否为数字
bool isNumber(const string& s) {
	if (s[0] == '+' || s[0] == '-' ||
		s[0] == '*' || s[0] == '/') {
		return false;
	}

	return true;
}

// 执行一次运算
double applyOp(double a, double b, const string& op) {
	if (op == "+") return a + b;
	if (op == "-") return a - b;
	if (op == "*") return a * b;
	if (op == "/") {
		if (b == 0) throw runtime_error("除零错误");
		return a / b;
	}

	throw runtime_error("未知运算符：" + op);
}

// 计算逆波兰表达式(后缀表达式)
double evalRPN(const string& expr) {
	stack<double> st;
	stringstream ss(expr);
	string token;

	while (ss >> token) {
		if (isNumber(token)) {
			st.push(stod(token));
		} else {
			if (st.size() < 2) throw runtime_error("表达式错误，操作数不足");
			
			double b = st.top(); st.pop();
			double a = st.top(); st.pop();
			st.push(applyOp(a, b, token));
		}
	}

	if (st.size() != 1) throw runtime_error("表达式错误：栈中剩余元素不为1");
	return st.top();
}

int main() {
	try {
		string expr1 = "3 4 +";          // => 7
		string expr2 = "3 4 2 * +";      // => 11
		string expr3 = "3 5 + 2 *";      // => 16
		string expr4 = "10 2 8 * + 3 -"; // => 23

		cout << expr1 << " = " << evalRPN(expr1) << endl;
		cout << expr2 << " = " << evalRPN(expr2) << endl;
		cout << expr3 << " = " << evalRPN(expr3) << endl;
		cout << expr4 << " = " << evalRPN(expr4) << endl;
	}
	catch (const exception& e) {
		cout << "错误: " << e.what() << endl;
	}
	return 0;
}

输出结果：

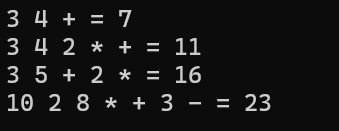
六、中缀表达式转为后缀表达式

基本思想（使用栈 Stack）

使用两个序列：

  1. 输出序列：存放生成的后缀表达式
  2. 运算符栈：存放操作符（+ − * / ( ) 等）

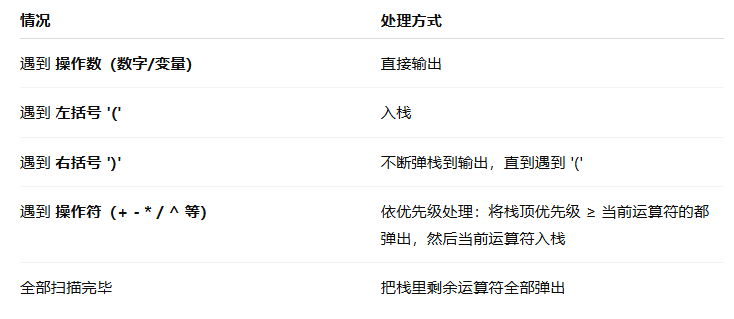
核心规则：

运算符优先级

设定一个函数：

cpp 复制代码 
^        // 最高，幂
* /      // 其次
+ -      // 最低

举例说明

中缀表达式：

cpp 复制代码 
A + B * C - (D - E) * F

转换过程（略），最终后缀表达式：

cpp 复制代码 
A B C * + D E - F * -

实现代码：

cpp 复制代码 
#include <iostream>
#include <stack>
#include <string>
using namespace std;

// 返回运算符优先级
int precedence(char op) {
    if (op == '^') return 3;
    if (op == '*' || op == '/') return 2;
    if (op == '+' || op == '-') return 1;
    return 0;
}

// 中缀表达式转换为后缀表达式
string infixToPostfix(const string& exp) {
    stack<char> st;
    string output;

    for (char c : exp) {
        // 1. 操作数：直接输出
        if (isalnum(c)) {
            output += c;
        }
        // 2. 左括号：入栈
        else if (c == '(') {
            st.push(c);
        }
        // 3. 右括号：弹出直到 '('
        else if (c == ')') {
            while (!st.empty() && st.top() != '(') {
                output += st.top();
                st.pop();
            }
            st.pop();  // 弹出 '('
        }
        // 4. 运算符：依优先级处理
        else {
            while (!st.empty() && precedence(st.top()) >= precedence(c)) {
                output += st.top();
                st.pop();
            }
            st.push(c);
        }
    }

    // 5. 剩余运算符全部弹出
    while (!st.empty()) {
        output += st.top();
        st.pop();
    }

    return output;
}

int main() {
    string exp = "A+B*C-(D-E)*F";
    cout << "中缀:   " << exp << endl;
    cout << "后缀:   " << infixToPostfix(exp) << endl;
    return 0;
}

输出结果：

相关推荐
xlq223224 小时前
15.list（上）
数据结构·c++·list
我不会插花弄玉4 小时前
排序【由浅入深-数据结构】
c语言·数据结构
XH华5 小时前
数据结构第三章：单链表的学习
数据结构
Knox_Lai6 小时前
数据结构与算法学习(0)-常见数据结构和算法
c语言·数据结构·学习·算法
blammmp7 小时前
算法专题二十：贪心算法
数据结构·算法·贪心算法
小白程序员成长日记7 小时前
2025.11.17 力扣每日一题
数据结构·算法·leetcode
时间醉酒9 小时前
数据结构：栈详解-从原理到实现（顺序栈与链式栈）
c语言·数据结构·c++·算法·链表
立志成为大牛的小牛9 小时前
数据结构——四十八、B树(王道408)
数据结构·笔记·b树·学习·考研·算法
大千AI助手9 小时前
二叉树：机器学习中不可或缺的数据结构
数据结构·人工智能·机器学习·二叉树·tree·大千ai助手·非线性数据结构
热门推荐
01GitHub 镜像站点02今天 Cloudflare 全球事故，连 GPT 和你的网站都一起“掉线”了03UV安装并设置国内源04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05BongoCat - 跨平台键盘猫动画工具06Linux下V2Ray安装配置指南07全球最强模型Grok4，国内已可免费使用！（附教程）08Valdi：Snapchat 开源的新一代跨平台 UI 框架09Labelme从安装到标注：零基础完整指南10swagger xss漏洞复现