文章目录
前言
咋知道这个AI生成坏了,没法用,那简单概括一下,就是B树的定义和性质
一.5叉查找树
1.结构
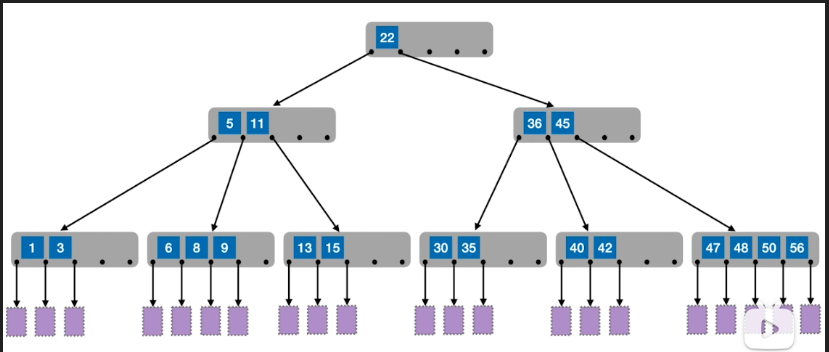
- 有点像分块查找,将要查找的元素按每5个一块的方式分开,然后从最中间的1~4个元素为根结点进行构建5叉树
- 在使用的时候先将要查找的元素在结点内进行查找(顺序或折半查找),如果找到,则返回,如果没找到,则进入下一层(如果能进入)
2.代码定义
c
//5叉排序树的结点定义
struct Node {
Element keys[4]; //最多4个关键字
struct Node * child[5]; //最多5个孩子
int num; //结点中有几个关键字
};二.如何保证查找效率
1.控制各个节点关键字的个数
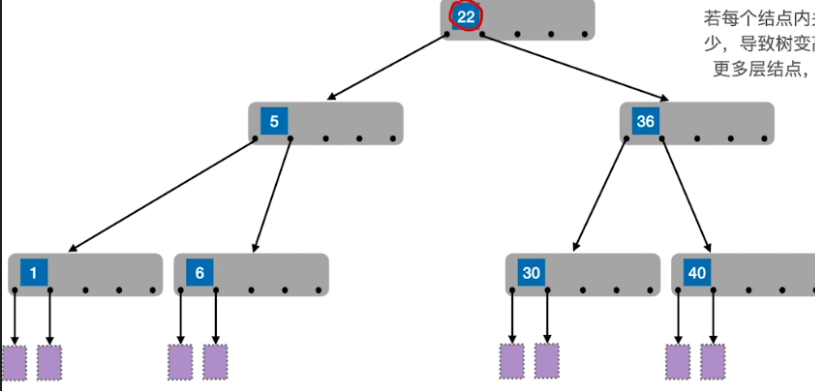
- 若每个结点内关键字太少,导致树变高,要查更多层结点,效率低
- 策略:m叉查找树中,规定除了根节点外,任何结点至少有 ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉ 个分叉,即至少含有 ⌈ m / 2 ⌉ − 1 \lceil m/2 \rceil-1 ⌈m/2⌉−1 个关键字
为什么规定除了根结点之外,因为假设整个树只有一个元素,那么其根结点就只能有两个分叉
2.控制子树高度差
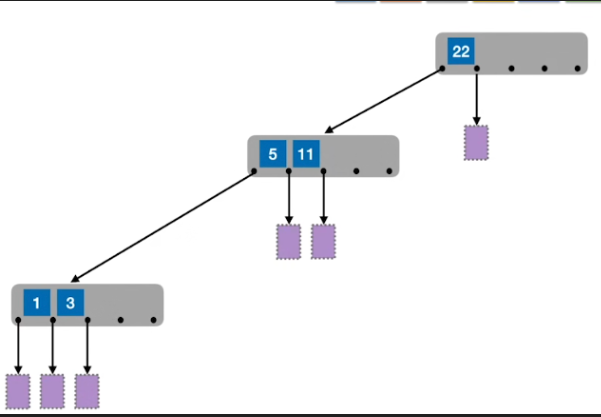
- 不够"平衡",树会很高,要查很多层结点
- 策略:m叉查找树中,规定对于任何一个结点,其所有子树的高度都要相同。
三.B树(多路平衡查找树)
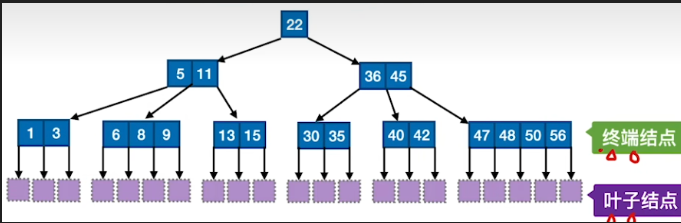
1.定义
- B 树 ,又称多路平衡查找树 ,B 树中所有结点的孩子个数的最大值称为 B 树的阶,通常用 m 表示。一棵 m 阶 B 树或为空树,或为满足如下特性的 m 叉树:
- 树中每个结点至多有 m 棵子树,即至多含有 m-1 个关键字。
- 若根结点不是终端结点,则至少有两棵子树。
- 除根结点外 的所有非叶结点至少 有 ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉ 棵子树,即至少 含有 ⌈ m / 2 ⌉ − 1 \lceil m/2 \rceil-1 ⌈m/2⌉−1 个关键字。
- 所有非叶结点的结构如下:
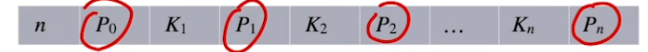
其中, K i ( i = 1 , 2 , ... , n ) K_{i}(i=1,2,\dotsc,n) Ki(i=1,2,...,n)为结点的关键字,且满足 K 1 < K 2 < ... < K n ; P i ( i = 0 , 1 , ... , n ) K1<K2< \dotsc < Kn; P i(i=0,1, \ldots,n) K1<K2<...<Kn;Pi(i=0,1,...,n)为指向子树根结点的指针,且指针Pi-1所指子树中所有结点的关键字均小于Ki ,Pi所指子树中所有结点的关键字均大于Ki , n ( ⌈ m / 2 ⌉ − 1 ⩽ n ⩽ m − 1 ) n(\lceil m/2\rceil-1 \leqslant n \leqslant m-1) n(⌈m/2⌉−1⩽n⩽m−1)为结点中关键字的个数。 - 所有的叶结点都出现在同一层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失败结点,实际上这些结点不存在,指向这些结点的指针为空).
2.通俗理解
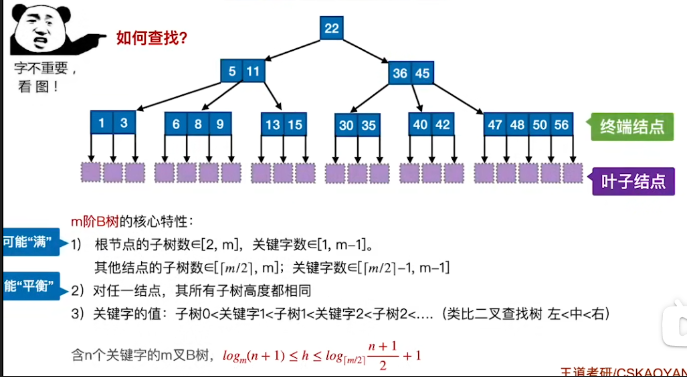
- 满足以下两个条件的m叉查找树称为B树
- m叉查找树中,规定对于任何一个结点,其所有子树的高度都要相同
- m叉查找树中,规定除了根节点外,任何结点至少有 ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉ 个分叉,即至少含有 ⌈ m / 2 ⌉ − 1 \lceil m/2 \rceil-1 ⌈m/2⌉−1 个关键字
- 关键字的值:子树0<关键字1<子树1<关键字2<子树2<......(类比二叉查找树左<中<右)
- 其中,失败结点(空指针)被称为叶子结点 ,原本的叶子结点被称为终端结点
四.B树的高度
1.书中的证明方法(h+1层最少结点的个数证明)
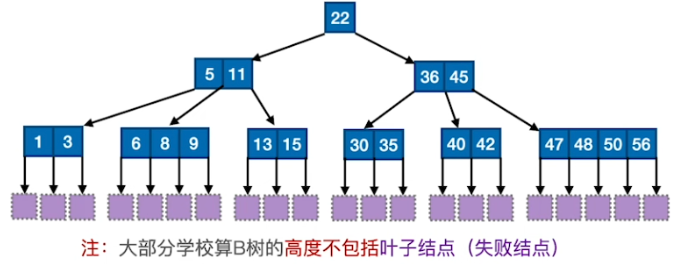
-
问题:含n个关键字的m阶B树,最小高度、最大高度是多少?
答:
- 最小高度------让每个结点尽可能的满,有m-1个关键字,m个分叉,则有 n ≤ ( m − 1 ) ( 1 + m + m 2 + m 3 + ⋯ + m h − 1 ) = m h − 1 n\le(m-1)(1+m+m^{2}+m^{3}+\cdots +m^{h-1})=m^{h}-1 n≤(m−1)(1+m+m2+m3+⋯+mh−1)=mh−1,因此 h ≥ log m ( n + 1 ) h\ge\log_{m}(n+1) h≥logm(n+1)
- 最大高度------让各层的分叉尽可能的少,即根节点只有 2 个分叉,其他结点只有 ⌈ m / 2 ⌉ \lceil m/2\rceil ⌈m/2⌉个分叉
各层结点至少有:第一层:1,第二层:2,第三层: 2 ⌈ m / 2 ⌉ 2\lceil m/2\rceil 2⌈m/2⌉...,第h层: 2 ( ⌈ m / 2 ⌉ ) h − 2 2(\left\lceil m/2 \right\rceil)^{h-2} 2(⌈m/2⌉)h−2个
第h+1层共有叶子结点(失败结点) 2 ( ⌈ m / 2 ⌉ ) h − 1 2(\left\lceil m/2\right\rceil)^{h-1} 2(⌈m/2⌉)h−1个
n 个关键字的 B 树必有 n+1 个叶子结点 ,则 n + 1 ≥ 2 ( ⌈ m / 2 ⌉ ) h − 1 n+1\ge 2(\left\lceil m/2\right\rceil)^{h-1} n+1≥2(⌈m/2⌉)h−1,即 h ≤ log ⌈ m / 2 ⌉ n + 1 2 + 1 h\le \log_{\lceil m/2\rceil}\frac{n+1}{2}+1 h≤log⌈m/2⌉2n+1+1
-
这里除了最大最小高度的计算公式外,还有高度为h(不带失败结点)的m阶B树的h+1层的结点的个数,最少是 2 ( ⌈ m / 2 ⌉ ) h − 1 2(\left\lceil m/2\right\rceil)^{h-1} 2(⌈m/2⌉)h−1个
2.视频里的证明方法(最少关键字个数证明)
- 问题:含n个关键字的m叉B树,最小高度、最大高度是多少?
- 最大高度------让每个结点包含的关键字、分叉尽可能的少。记 k = ⌈ m / 2 ⌉ k=\lceil m/2\rceil k=⌈m/2⌉(最小分叉数量)
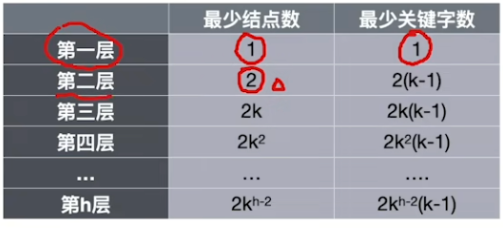
- h层的m阶B树至少包含关键字总数 1 + 2 ( k − 1 ) ( k 0 + k 1 + k 2 + ... + k h − 2 ) = 1 + 2 ( k h − 1 − 1 ) 1+2(k-1)(k^{0}+k^{1}+k^{2}+\dotsc +k^{h-2})=1+2(k^{h-1}-1) 1+2(k−1)(k0+k1+k2+...+kh−2)=1+2(kh−1−1)
若关键字总数少于这个值,则高度一定小于h,因此 n ≥ 1 + 2 ( k h − 1 − 1 ) n≥1+2(k^{h-1}-1) n≥1+2(kh−1−1)
得, h ≤ log k n + 1 2 + 1 = log ⌈ m / 2 ⌉ n + 1 2 + 1 h\le \log_{k}\frac{n+1}{2}+1=\log_{\lceil m/2\rceil }\frac{n+1}{2}+1 h≤logk2n+1+1=log⌈m/2⌉2n+1+1
3.结论
- 含n个关键字的m叉B树, l o g m ( n + 1 ) ≤ h ≤ log ⌈ m / 2 ⌉ n + 1 2 + 1 log_{m}(n+1)≤h≤\log_{\lceil m/2\rceil }\frac{n+1}{2}+1 logm(n+1)≤h≤log⌈m/2⌉2n+1+1
- h层的m阶B树至少包含关键字总数, n ≥ 1 + 2 ( k h − 1 − 1 ) n≥1+2(k^{h-1}-1) n≥1+2(kh−1−1)
- 高度为h(不带失败结点)的m阶B树的h+1层的结点的个数,最少是 2 ( ⌈ m / 2 ⌉ ) h − 1 2(\left\lceil m/2\right\rceil)^{h-1} 2(⌈m/2⌉)h−1个
五.知识回顾与重要考点
结语
四更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页