数据结构之排序-插入排序

前言

在上一篇文章数据结构之二叉树-链式结构(下)我们将二叉树相关方法实现的剩下部分进行了讲解，还讲解了有关二叉树非常经典的OJ题，到此初阶数据结构的二叉树我们就讲解完了，为什么说是初阶呢？原因是二叉树其实我们还没有学习完，等到后面讲解C++时二叉树还会讲解新的内容，只是现在先告一段落。

而这次我们就要讲解初阶数据结构中最后一个内容-排序，排序不管是在数据结构中还是算法中都是尤为重要的，内容量也是非常之多，单分类就有插入排序 、选择排序 、交换排序 以及归并排序，当我们把排序讲完初阶数据结构也就学习完了，也就要开始步入C++的学习当中了。本篇文章主要讲解的是排序中的插入排序。

一、排序的概念及应用

1、排序的概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

2、排序的应用

购物筛选排序

院校排名

我们会发现不管是日常生活上的购物还是学校之间的排名，都有着排序的影子，说到底我们日常生活一直都跟排序打交道，这也侧面体现出排序的重要性。

常见排序算法

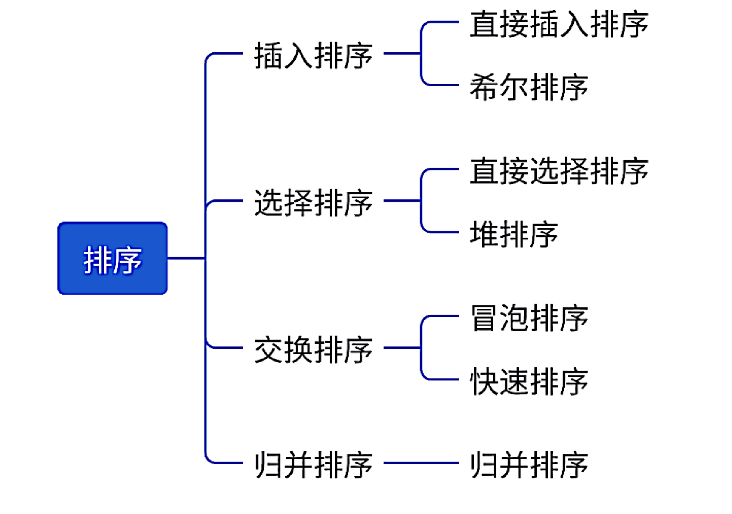
在前言我们已经提到了排序总共分为四类，但这四类又可以细分这些排序，这篇文章主要就是讲解插入排序中的直接插入排序 以及希尔排序。

插入排序

一、直接插入排序

1、基本思想和逻辑

直接插入排序 是一种简单的插入排序法，其基本思想是：把待排序的记录 按其关键码值的大小 逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列。

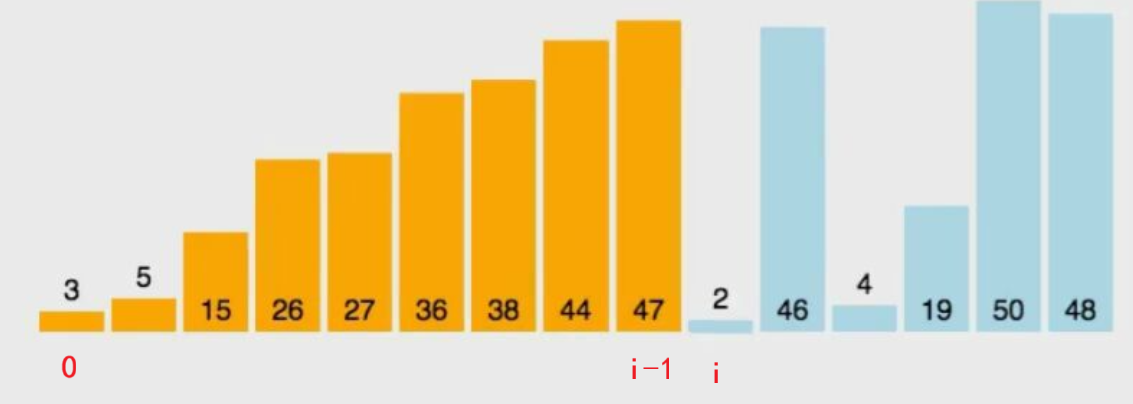
当插入第 i ( i > =1 ) 个元素 时，前面的array [ 0 ] ，array [ 1 ] ，... ，array [ i - 1] 已经排好序 ，此时用 array [ i ] 的排序码与 array [ i - 1 ] ，array [ i - 2 ] ，...的排序码顺序进行比较，找到插入位置即可将 array [ i ] 插入，原来位置上的元素顺序后移。

2、代码实现

cpp 复制代码

//Sort.h
#include <stdio.h>
#include <stdlib.h>
//直接插入排序
void InsertSort(int* arr, int n);

//Sort.c
//直接插入排序
void InsertSort(int* arr, int n)
{
	for (int i = 0; i < n - 1; i++)
	//这里的 i < n-1 而不是 i < n 原因在于我们的 end 为 i，
    //而[0, end]已经有序，我们需要排序的是arr[end + 1]
	//所以 i = n - 2 时，就相当于数组最后一个数进行排序了
	{
		int end = i;
		//令[0, end]已经有序，则每次将 end+1 位置的值通过比较插入到[0, end]中，保持有序
		int tmp = arr[end + 1]; 
		//将准备插入到[0, end]中的arr[end + 1]先保存到一个变量中，
        //因为在比较时前面的值可能会覆盖当前位置

		while (end >= 0)
		{
			if (arr[end] > tmp)
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else
			{
				break;
			}
		}
		arr[end + 1] = tmp; 
        //这个代码不放到else里面原因是：当一个需要排序的数一直判断到end为0
		//也就是说与排好序的第一个数比较，如果还是第一个数大也就是说排序的数要放到开头
	    //则第一个数也要往后移一位然后end--，此时end就为-1了，跳出循环，这样就不能插入要排序的数
	}
}

3、打印测试代码

cpp 复制代码

//Test.c
#include "Sort.h"
void Test()
{
	int arr[9] = { 3, 8, 5, 1, 6, 9, 2, 7, 4 };
	InsertSort(arr, sizeof(arr) / sizeof(arr[0]));
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]) ; i++)
	{
		printf("%d ", arr[i]);
	}
}

int main()
{
	Test();
	return 0;
}

直接插入排序的特性总结

(1)元素集合越接近有序，直接插入排序算法的时间效率越高

(2)时间复杂度：最坏情况(逆序)：

最好情况(顺序)：

(3)空间复杂度：

二、希尔排序

1、希尔排序的概念介绍

希尔排序法 又称缩小增量法 。希尔排序法的基本思想是：先选定一个整数(通常是gap = n / 3 + 1) ，把待排序文件所有记录分成各组 ，所有的距离相等的记录分在同一组内 ，并对每一组内的记录进行排序，然后gap = gap / 3 + 1得到下一个整数，再将数组分成各组，进行插入排序，当gap = 1时，就相当于直接插入排序。

首先看到希尔排序的介绍大家一下就懵了，突然来了一堆莫名其妙的东西什么gap，什么n/3+1，什么分组排序乱七八糟的，所以接下来我就为大家一一解释希尔排序到底在做什么。

2、希尔排序的作用

当我们学习完上面的直接插入排序会发现：当一个数组比较接近有序的 时候直接插入排序是挺有用的 ，但是假设一个数组是完全逆序也就是最坏情况的时候，每次要排序的数字都需要一直判断到开头才能插入，使得时间复杂度为，这种复杂度不是我们能接受的，所以希尔排序就出现了。

希尔排序其实就是在直接插入排序算法的基础上进行改进而来的，所以综合来说它的效率肯定是要高于直接插入排序算法的。

3、希尔排序的逻辑

那希尔排序到底是怎么改进的呢？

首先希尔排序分成两个步骤：(1)预排序(让数组接近有序)；(2)插入排序

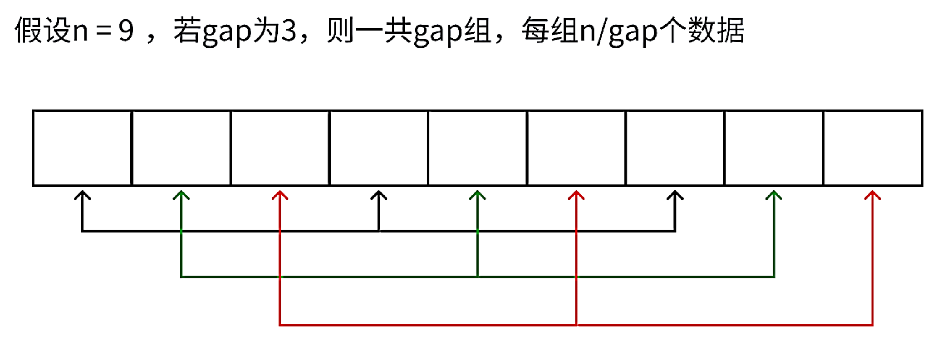
在步骤一也就是预排序中，定义了一个整数gap，这个gap的意思是：将每两个距离为gap的数分为一组，假设gap = 3，如下图：

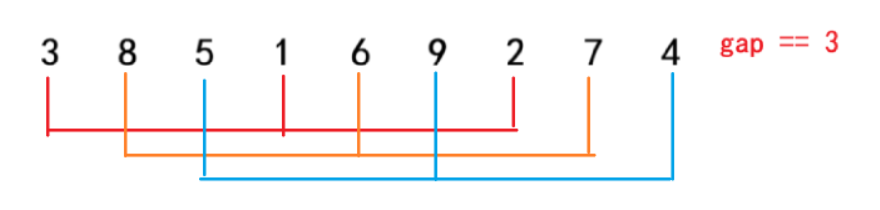
看到这个图大家应该就对gap这个东西理解了一些了，并且看图我们就能提前得到一个小结论：当gap为多少，就被分为多少组 。这个不难证明，原因是假设gap = 3时，下标为0和下标为3的数其实就是第一组，这样的话下标为1以及下标为2的就分别是不同组了，这样总共就被分成三组了。

然后我们对每一组的数据进行排序，这样就会使得整个数组会变得比较有序了。

4、希尔排序的代码实现

4.1 单组排序的代码实现

由于希尔排序比较复杂，我们就将整个代码分开进行讲解，在实现预排序之前我们先把每一组的排序代码实现一遍我们就以gap = 3为例：

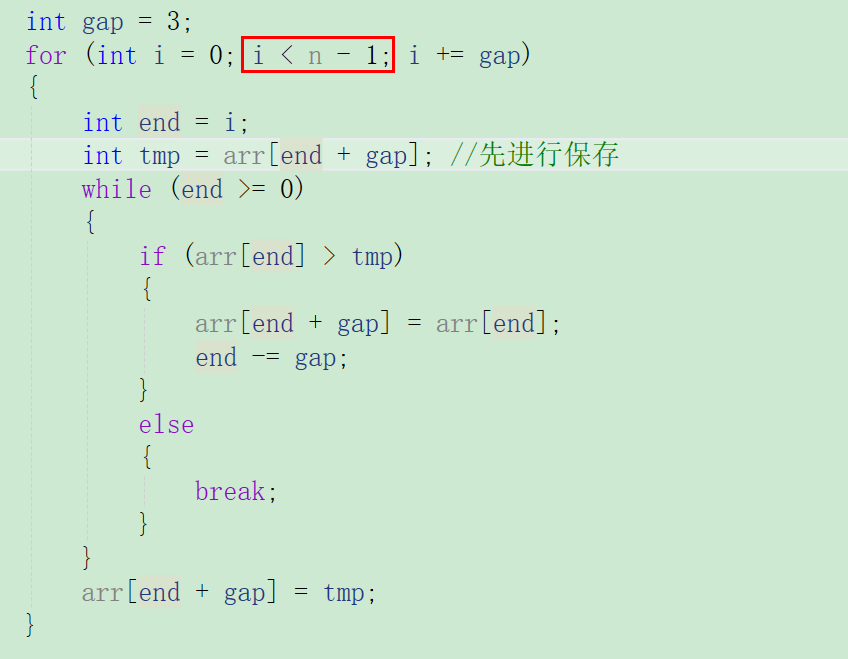
上面代码就是第一组进行排序的逻辑，但是这个代码并不是完全正确的，而错误的地方就是我框起来的位置。为什么i < n - 1会有问题呢？

我们还是以上面的例子进行解释：

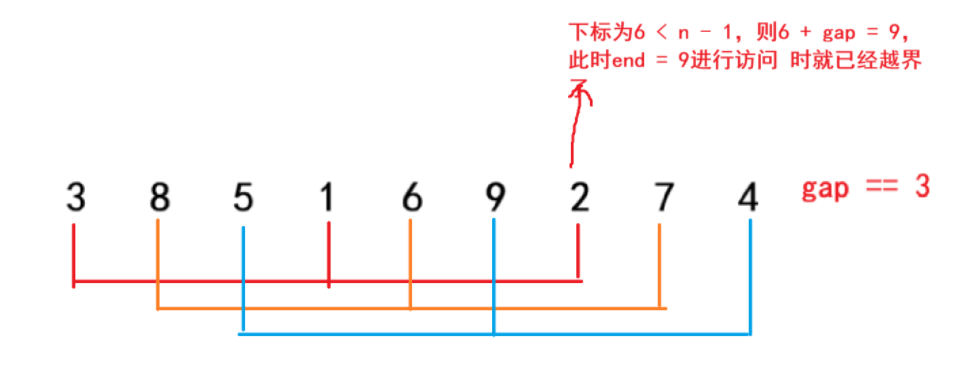
所以为了让所有组都能实现排序，i 的限制范围就不能还是n - 1了，而是n - gap，当i < n - gap时，就能保证每个组都不会有越界访问的情况了。

4.2 多组排序的代码实现

4.2.1 方法一：每组依次排序

看到上面图我们会发现实现第一组排序 也就是以下标为0作为第一个数的一组进行排序 ，所以不难发现当我们的i 的初始值在变就相当于不同的组进行排序，则代码如下：

这个代码逻辑就是 j 为0时就是第一组进行排序，排完序 j 变成1，则就是第二组进行排序，以此类推把每一组都分别排好序我们也就完成了预排序 。

但是我们会发现这个代码是有三层循环 的，其实并不是很美观 ，所以我们想到了另一种排序的方法：多组同时排序。

4.2.2 方法二：多组同时排序

多组同时排序的逻辑不容易理解，但是会少一个循环代码。首先我们对第一组的前两个数(下标为0和3)进行排序，当这两个数排好序后按照方法一的逻辑就是继续第一组的第三个数进行排序，但是这里不同：接着我们对第二组的前两个数(下标为1和4)进行排序，排好序后我们就对第三组的前两个数(下标为2和5)进行排序。

排好序后我们会发现当下标来到3时不就变成第一组的第三个数进行排序了吗？而且我们会发现 i 也并不是像方法一那样为 i += gap 跳着取值，而是 i++ ，这样我们也就实现了三组同时进行排序的逻辑。代码如下：

一般而言用方法二会多一点，虽然两种方法的消耗是完全一样的，但主要是方法二只有两层循环会显得更加美观，具体用哪种方法还是看个人喜好。

4.3 gap取值问题

当我们把多组排序实现完后，我们想一下预排序就可以结束而开始实现步骤二的插入排序吗？

当学习了上面的知识后对于预排序 我们会发现一个特点：

(1)当gap越大，所分的组就越多，每组数据的个数越少，每组数据之间的距离越大。
优点：使得大的数越快跳到后面，小的数越快跳到前面；
缺点：各组排好序后整体越不接近有序
(2)当gap越小，所分的组就越少，每组数据的个数越多，每组数据之间的距离越小。
缺点：使得大的数越慢跳到后面，小的数越慢跳到前面；
优点：各组排好序后整体越接近有序

那就有一个问题摆在我们面前：到底gap取多大合适呢？取过大的话就会导致预排序没多大用处(整体仍然不接近有序)；取过小的话就会导致基本接近直接插入排序的效果，时间复杂度仍然很大。

所以希尔这个人就考虑进行多次预排序并且gap是不断变化的，那gap怎么变化呢？一开始希尔这个人想到的是每次取半即gap = gap / 2。并且我们会发现非常巧妙的是：当gap一直取半时总有一次gap = 1 ，而gap = 1其实就是直接插入排序的代码。 所以希尔这个让gap不断变化的方法不仅能优化排序效率还能同时解决预排序和插入排序两个步骤。

4.3.1 gap = gap / 2的希尔排序展示

cpp 复制代码

//Sort.h
#include <stdio.h>
#include <stdlib.h>

//打印数组
void PrintArray(int* arr, int n);

//希尔排序
void ShellSort(int* arr, int n);

//Sort.c
//希尔排序
void ShellSort(int* arr, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 2;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = arr[end + gap]; //先进行保存
			while (end >= 0)
			{
				if (arr[end] > tmp)
				{
					arr[end + gap] = arr[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			arr[end + gap] = tmp;
		}
		printf("gap：%2d->", gap);
		PrintArray(arr, n);
	}
}

//Test.c
void Test()
{
	int arr[] = { 3, 8, 5, 1, 6, 9, 2, 10, 7, 4 };

	PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
	ShellSort2(arr, sizeof(arr) / sizeof(arr[0]));
	PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}

int main()
{
	Test();
	return 0;
}

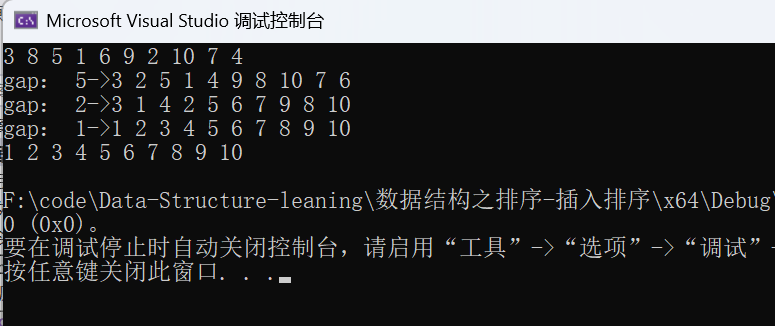
通过每次gap变化时打印的数组结果我们会发现希尔这个想法是正确的，为什么说是正确的呢？

就像最开始说的那样，当gap只取一次，如果gap取得过大，好处虽然是大的数字更快排到后面但缺点就是这个数组越不有序；如果gap取得过小，好处虽然是这个数组更有序但循环次数更多时间复杂度更大。

而如打印结果所示：第一次gap = 5时，此时gap值较大 ，则大的数更快到后面小的数更快到前面 ，但明显此时整个数组仍然显得不是很有序 ；第二次gap = 2时，此时gap值就较小 了，但由于第一次的排序 会使得第二次排序的循环次数不会那么多 ，并且会使整个数组更加趋于有序的状态 ；而当第三次gap = 1时则就是直接插入排序 了，此时的数组 其实已经接近有序 的了，所以直接插入排序所循环的次数也就很少了 。

这个方法就有点类似于生活中的磨刀，一开始磨刀我们会使用比较粗的磨刀石，先快速的进行磨刀，缺点就是磨的刀不精细，当磨了一会后再改用更细的磨刀石进行打磨，虽然磨刀的时间变长了但会使刀更加精细。两者的结合就能使刀不仅磨的快还锋利。这样大家对希尔这个gap一直变化来排序的思路应该就清楚了。

4.3.2 gap = gap / 3 + 1的展示及两者对比

当希尔想到这个方法后，肯定有些人会说难道只能每次取半吗？所以后来的人就通过一系列数学专业的方法证明希尔这个gap取值并不是最优的，而是有另一个取值方式： gap = gap / 3 + 1，这个方式进行取值的效率是优与取半的方式。

首先我们给出这个希尔排序的代码：

cpp 复制代码

//Sort.c
//希尔排序
void ShellSort1(int* arr, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = arr[end + gap]; //先进行保存
			while (end >= 0)
			{
				if (arr[end] > tmp)
				{
					arr[end + gap] = arr[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			arr[end + gap] = tmp;
		}
		printf("gap：%2d->", gap);
		PrintArray(arr, n);
	}
}

那我们怎么证明第二种方式会优于第一种方式呢？这里我们就利用到一个关键字为 clock ，这个关键字的作用是计算从程序开始运行到执行这个代码之间的时间 (单位：毫秒)，所以我们可以利用这个关键字来计算执行完希尔排序所用的时间：

cpp 复制代码

//Test.c
#include <time.h>

void Test2()
{
	srand((unsigned int)time(NULL));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);

	for (int i = 0; i < N; i++)
	{
		a1[i] = rand() + i;
		a2[i] = a1[i];
	}

	int began1 = clock();
	ShellSort1(a1, N);
	int end1 = clock();

	int began2 = clock();
	ShellSort2(a2, N);
	int end2 = clock();

	printf("ShellSort(gap = n / 3 + 1)：%d\n", end1 - began1);
	printf("ShellSort(gap = n / 2)：%d\n", end2 - began2);

	free(a1);
	free(a2);
}

int main()
{
	Test2();
	return 0;
}

这个代码的逻辑就是通过随机值取100000个数据同时给两个数组，一个数组执行方式一的希尔排序，一个数组执行方式二的希尔排序，然后打印出两者所消耗的时间进行对比：

我们会发现用方式二进行的希尔排序所消耗时间为10毫秒而方式一所消耗的时间为13毫秒，之所以会这么短是因为计算机跑程序是非常快的，对于十万数据的程序几乎就是瞬间完成，但通过对比我们还是会发现方式二的效率的确优于方式一。

5、希尔排序的时间复杂度

首先的外层循环(也就是gap变化的循环)：

由于gap是每次除2或除3，所以外层循环的时间复杂度就很容易知道为：

或者，即

而内层的时间复杂度就很难证明了：

假设一共有 n 个数据，合计 gap 组，则每组为 n/gap 个；在每组中，插入移动的次数最坏的情况下为：，一共是gap组，因此：

总计最坏情况下移动总数为：

gap取值有(以除3为例)：n/3、n/9、n/27、.....、2、1

(1)当gap为 n/3 时，最坏情况移动总数为：

(2)当gap为 n/9 时，最坏情况移动总数为：

(3)当最后一趟，gap = 1即直接插入排序时，由于此时数组已经非常接近有序了，则循环排序消耗为 n。

通过以上的分析，我们可以大致画出这样的曲线图：

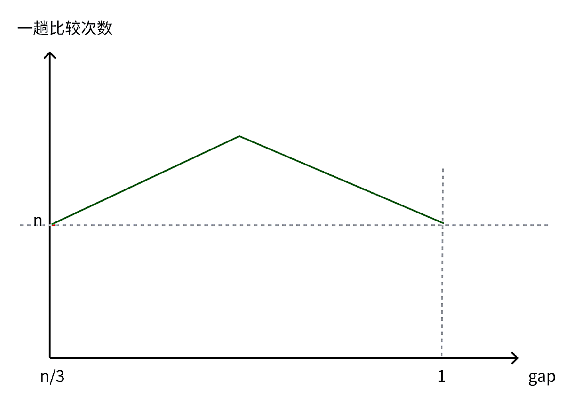
因此，希尔排序在最初和最后的排序的次数都为n，即前一阶段排序次数是逐渐上升的状态，当到达某一顶点时，排序次数逐渐下降至n，而该顶点的计算暂时无法给出具体的计算过程。

所以因为这个原因导致不同的书给出的希尔排序时间复杂度并不固定，在《数据结构(C语言版)》-- 严蔚敏的书中给出的时间复杂度为：

结束语

到此排序中的插入排序就讲解完了，直接插入排序还是非常简单易懂的，但希尔排序在整个排序方法中其实都算是很难理解的，看完上面的讲解其实就知道了。但我应该把希尔排序讲解的挺详细了，下一篇文章我就会为大家讲解排序中的选择排序以及交换排序。希望对大家学习排序能有所收获！