基于Matlab的五相永磁同步电机数学模型与矢量控制 五相 PMSM 矢量控制的关键是建立旋转坐标系下电机的数学模型,选择合适的派克变换矩阵,建立五相PMSM 在旋转坐标系下的数学模型,基于此模型进行五相 PMSM 矢量控制策略 利用 MATLAB 的 Simulink 建立五相 PMSM 矢量控制系统的仿真模型,进行仿真研究 程序已调通,可直接运行
在电机控制领域,五相永磁同步电机(PMSM)凭借其诸多优势越来越受到关注。而实现其高效控制的关键,就在于建立准确的数学模型以及合适的矢量控制策略,Matlab在这个过程中成为了得力助手。
建立旋转坐标系下的数学模型
五相PMSM矢量控制的核心,首先是要搭建旋转坐标系下电机的数学模型。这其中,选择恰当的派克变换矩阵至关重要。通过派克变换,我们可以将电机在静止坐标系下的复杂模型转换到旋转坐标系中,从而简化分析与控制。
假设五相PMSM的定子电压方程在静止坐标系下可以表示为:
\[
\begin{bmatrix}
u_{a} \\
u_{b} \\
u_{c} \\
u_{d} \\
u_{e}
\end{bmatrix}
=
\begin{bmatrix}
R & 0 & 0 & 0 & 0 \\
0 & R & 0 & 0 & 0 \\
0 & 0 & R & 0 & 0 \\
0 & 0 & 0 & R & 0 \\
0 & 0 & 0 & 0 & R
\end{bmatrix}
\begin{bmatrix}
i_{a} \\
i_{b} \\
i_{c} \\
i_{d} \\
i_{e}
\end{bmatrix}
p
\begin{bmatrix}
\psi_{a} \\
\psi_{b} \\
\psi_{c} \\
\psi_{d} \\
\psi_{e}
\end{bmatrix}
\]
其中 \( u \) 是相电压,\( i \) 是相电流,\( R \) 是定子电阻,\( p \) 是微分算子,\( \psi \) 是磁链。
经过派克变换,转换到旋转坐标系 \( d - q \) 下,其数学模型会发生相应变化。派克变换矩阵 \( T \) 形式如下(这里以五相为例,具体形式可能因不同的定义方式有所差异):
\[
T =
\begin{bmatrix}
\cos(\theta) & \cos(\theta - \frac{2\pi}{5}) & \cos(\theta - \frac{4\pi}{5}) & \cos(\theta + \frac{2\pi}{5}) & \cos(\theta + \frac{4\pi}{5}) \\
-\sin(\theta) & -\sin(\theta - \frac{2\pi}{5}) & -\sin(\theta - \frac{4\pi}{5}) & -\sin(\theta + \frac{2\pi}{5}) & -\sin(\theta + \frac{4\pi}{5}) \\
\cos(2\theta) & \cos(2(\theta - \frac{2\pi}{5})) & \cos(2(\theta - \frac{4\pi}{5})) & \cos(2(\theta + \frac{2\pi}{5})) & \cos(2(\theta + \frac{4\pi}{5})) \\
-\sin(2\theta) & -\sin(2(\theta - \frac{2\pi}{5})) & -\sin(2(\theta - \frac{4\pi}{5})) & -\sin(2(\theta + \frac{2\pi}{5})) & -\sin(2(\theta + \frac{4\pi}{5})) \\
\frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}} & \frac{1}{\sqrt{5}}
\end{bmatrix}
\]
通过这个变换矩阵,我们就能把静止坐标系下的方程转换到旋转坐标系 \( d - q \) 下,得到新的电压、电流和磁链关系,从而为后续的矢量控制策略奠定基础。
基于模型的矢量控制策略
基于上述建立的旋转坐标系下的数学模型,我们可以设计五相PMSM的矢量控制策略。矢量控制的目标是实现对电机转矩和磁链的解耦控制,从而达到类似直流电机的控制效果。
一般来说,在 \( d - q \) 坐标系下,我们可以通过控制 \( id \) 和 \( iq \) 电流分量来分别控制电机的磁链和转矩。通常令 \( i_d = 0 \),这样可以使电机在最大转矩/电流比的状态下运行,提高电机的效率。
以速度环和电流环双闭环控制为例,速度环输出作为电流环的给定值。速度环可以采用经典的PI控制器,代码示例如下(Matlab/Simulink伪代码):
matlab
% 速度环PI控制器参数
Kp_speed = 0.5;
Ki_speed = 10;
integral_speed = 0;
prev_error_speed = 0;
% 速度给定和反馈
speed_ref = 1000; % 速度给定值,单位rpm
speed_fb = get_speed_feedback(); % 获取速度反馈值的函数
error_speed = speed_ref - speed_fb;
integral_speed = integral_speed + error_speed * Ts; % Ts为采样时间
i_q_ref = Kp_speed * error_speed + Ki_speed * integral_speed + prev_error_speed;
prev_error_speed = error_speed;在电流环中,同样可以采用PI控制器来跟踪速度环输出的电流给定值 \( iq ref \) 和 \( id ref \)(一般 \( idref = 0 \)),以此来生成最终的PWM控制信号去驱动逆变器,控制电机的运行。
matlab
% 电流环PI控制器参数
Kp_current = 1;
Ki_current = 50;
integral_iq = 0;
prev_error_iq = 0;
% 电流反馈
i_q_fb = get_iq_feedback(); % 获取i_q电流反馈值的函数
error_iq = i_q_ref - i_q_fb;
integral_iq = integral_iq + error_iq * Ts;
u_q = Kp_current * error_iq + Ki_current * integral_iq + prev_error_iq;
prev_error_iq = error_iq;利用Simulink建立仿真模型
借助MATLAB的Simulink,我们能够轻松建立五相PMSM矢量控制系统的仿真模型,对上述控制策略进行仿真研究。在Simulink中,我们可以将电机模型模块、控制器模块、逆变器模块等进行合理连接,构建完整的系统。
比如,电机模型可以使用Simscape Electrical库中的永磁同步电机模型,根据实际电机参数进行设置。控制器模块则可以按照上述代码思路搭建速度环和电流环PI控制器。逆变器模块将控制器输出的电压信号转换为实际的PWM信号去驱动电机。
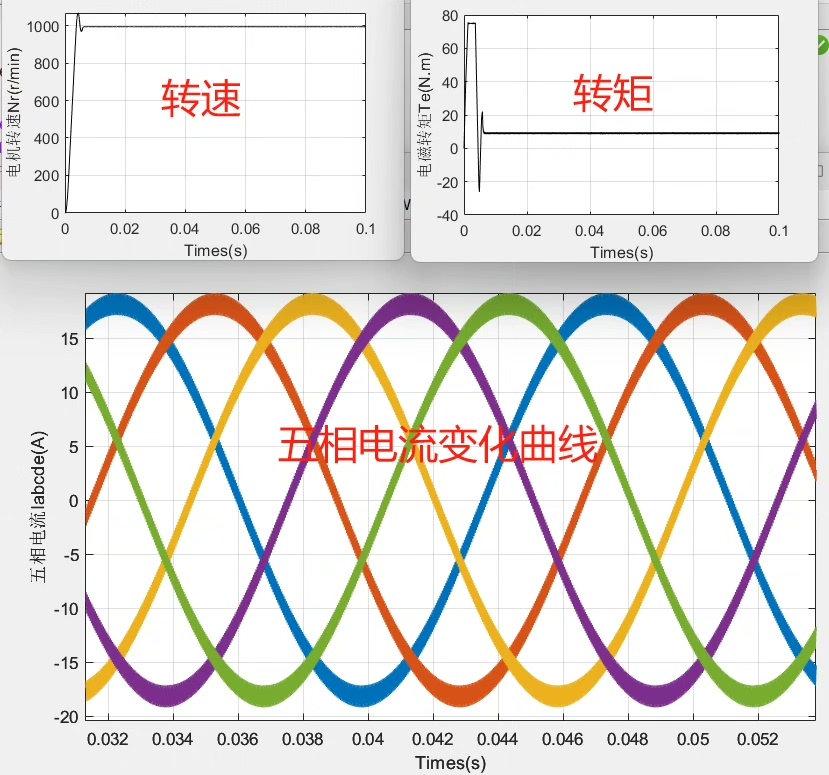
完成模型搭建后,运行仿真,我们就能直观地观察到电机的转速、转矩、电流等关键参数的变化情况,以此来验证我们所建立的数学模型和控制策略是否有效。幸运的是,本次程序已调通,可直接运行,这大大方便了我们对系统性能的分析与优化。
通过基于Matlab的五相永磁同步电机数学模型建立与矢量控制策略研究及仿真,我们能够更深入地理解五相PMSM的运行特性,并为实际应用中的电机控制提供有力的理论与实践支持。无论是在电动汽车、工业伺服系统等领域,五相PMSM都有望凭借其优势发挥更大的作用。