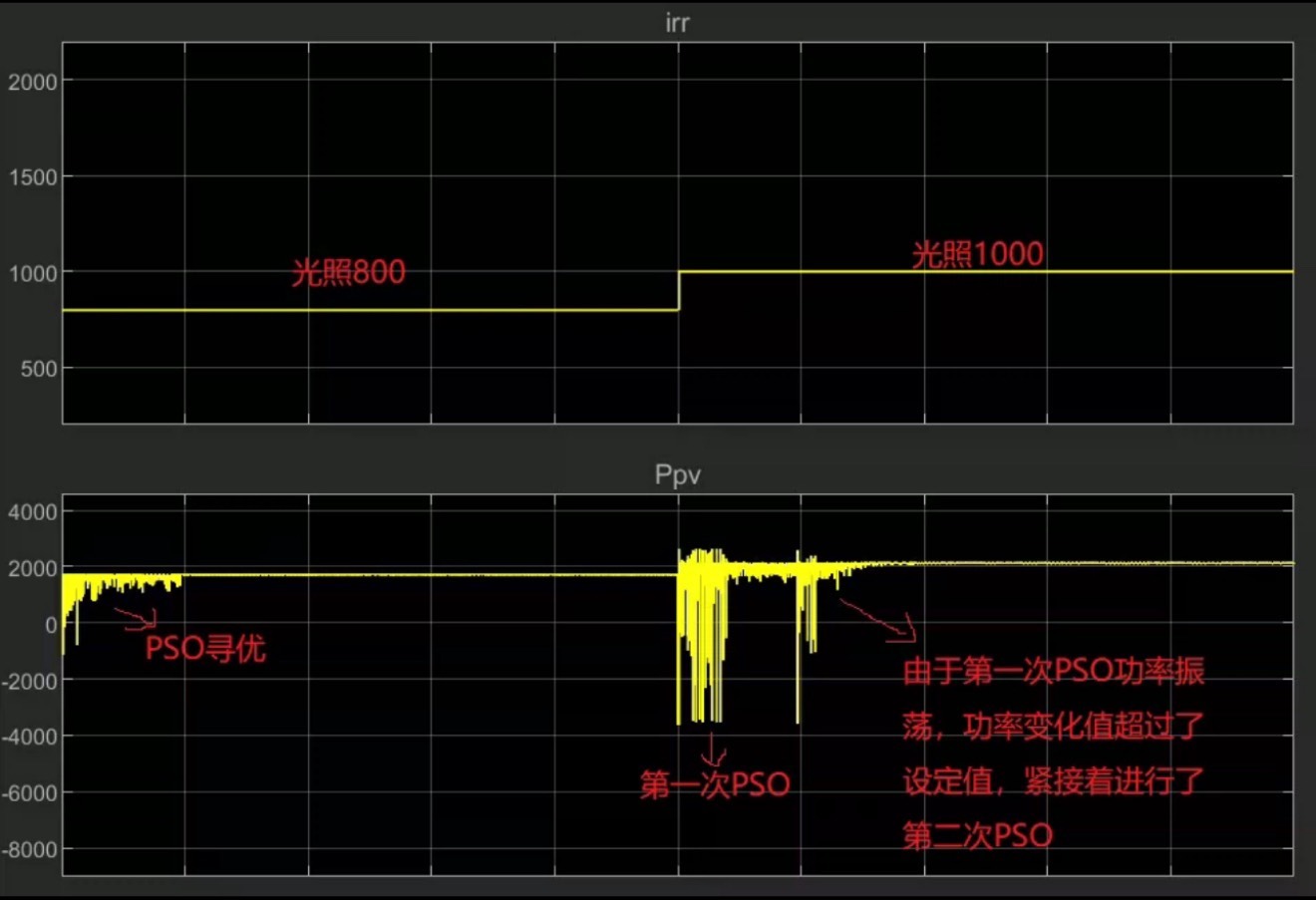
基于粒子群算法的光伏MPPT(可重启PSO) 光伏最大功率追踪算法模型simulink MPPT是基于粒子群算法实现的,同时具备动态追踪能力,当光照改变后会重启粒子群算法进行最大功率追踪
在光伏系统中,最大功率点跟踪(MPPT)技术至关重要,它能让光伏电池始终在最大功率点附近工作,提升发电效率。今天咱们就来唠唠基于粒子群算法(PSO)且具备可重启功能的MPPT。
粒子群算法与光伏MPPT
粒子群算法模拟鸟群觅食行为,每个粒子代表解空间中的一个潜在解,它们通过追踪自身历史最优位置(pbest)和种群全局最优位置(gbest)来更新自己的位置和速度,以此不断逼近最优解。
在光伏MPPT里,粒子的位置可以代表光伏电池的工作电压,通过调整这个"位置",也就是电压,让光伏电池输出功率最大化。
动态追踪与可重启PSO
实际应用中,光照条件不断变化。传统MPPT算法可能在光照突变时反应迟缓,无法迅速找到新的最大功率点。咱们这个基于可重启PSO的MPPT就不一样啦!一旦检测到光照改变,粒子群算法会重启,重新开始搜索最大功率点,实现动态追踪。
Simulink模型搭建
在Simulink里搭建这个模型,可以直观地看到算法运行过程。首先,需要构建光伏电池模型,模拟其输出特性。
matlab
% 简单的光伏电池模型示例
% 参数设置
Isc = 5; % 短路电流
Voc = 40; % 开路电压
n = 1.5; % 二极管品质因数
Rs = 0.5; % 串联电阻
Rsh = 1000; % 并联电阻
T = 298; % 温度
q = 1.6e - 19; % 电子电荷
k = 1.38e - 23; % 玻尔兹曼常数
% 计算光生电流
G = 1000; % 光照强度
Iph = Isc * G / 1000;
% 计算不同电压下的电流
V = 0:0.1:Voc;
I = Iph - Isc * (exp((q * (V + I * Rs)) / (n * k * T)) - 1) - (V + I * Rs) / Rsh;这段代码简单模拟了光伏电池在不同光照和温度下的电流 - 电压关系。通过调整光照强度 G 和温度 T 等参数,可以观察光伏电池输出特性的变化。
接着,搭建粒子群算法模块。粒子的速度更新公式如下:
\[ v*{i,d}(t + 1) = \omega v* {i,d}(t) + c1r {1,d}(t)(p*{i,d}(t) - x* {i,d}(t)) + c2r {2,d}(t)(gd(t) - x{i,d}(t)) \]
\[ x*{i,d}(t + 1) = x*{i,d}(t) + v_{i,d}(t + 1) \]
其中,\( v*{i,d} \) 是粒子 \( i \) 在维度 \( d \) 的速度,\( x* {i,d} \) 是粒子 \( i \) 在维度 \( d \) 的位置,\( \omega \) 是惯性权重,\( c1 \) 和 \( c 2 \) 是学习因子,\( r*{1,d} \) 和 \( r* {2,d} \) 是介于 \( 0 \) 到 \( 1 \) 之间的随机数,\( p*{i,d} \) 是粒子 \( i \) 的历史最优位置,\( g*d \) 是全局最优位置。
matlab
% 粒子群算法部分代码示例
% 初始化参数
nparticles = 50; % 粒子数量
ndimensions = 1; % 维度
maxiterations = 100; % 最大迭代次数
c1 = 1.5; % 学习因子1
c2 = 1.5; % 学习因子2
omega = 0.8; % 惯性权重
% 初始化粒子位置和速度
x = zeros(nparticles, ndimensions);
v = zeros(nparticles, ndimensions);
for i = 1:nparticles
x(i, :) = Voc * rand(1, ndimensions); % 初始位置在0到Voc之间随机
v(i, :) = 0.1 * rand(1, ndimensions); % 初始速度较小
end
% 初始化历史最优位置和全局最优位置
pbest = x;
pbest_fitness = zeros(nparticles, 1);
for i = 1:nparticles
pbest_fitness(i) = calculate_power(x(i, :)); % 计算初始适应度(功率)
end
[gbest_fitness, gbest_index] = min(pbest_fitness);
gbest = pbest(gbest_index, :);
% 迭代更新
for t = 1:maxiterations
for i = 1:nparticles
r1 = rand(1, ndimensions);
r2 = rand(1, ndimensions);
v(i, :) = omega * v(i, :) + c1 * r1.* (pbest(i, :) - x(i, :)) + c2 * r2.* (gbest - x(i, :));
x(i, :) = x(i, :) + v(i, :);
% 边界处理
x(i, x(i, :) < 0) = 0;
x(i, x(i, :) > Voc) = Voc;
fitness = calculate_power(x(i, :));
if fitness < pbest_fitness(i)
pbest_fitness(i) = fitness;
pbest(i, :) = x(i, :);
end
if fitness < gbest_fitness
gbest_fitness = fitness;
gbest = x(i, :);
end
end
end这段代码实现了粒子群算法的基本流程,不断更新粒子位置,寻找最优解(最大功率点对应的电压)。
光照检测模块可以通过传感器数据输入或者模拟光照突变信号来触发粒子群算法的重启。
总结
基于粒子群算法的可重启MPPT为光伏系统在复杂光照条件下高效运行提供了有力保障。通过Simulink模型搭建和代码实现,我们能更深入理解其工作原理和运行机制。希望这篇文章能给对光伏MPPT感兴趣的小伙伴们一些启发,大家一起探索更高效的光伏能源利用方案。
