基于ELM和DE-NSGA-III的齿盘切削参数优化方案
- 问题定义与核心思想
优化目标: 在齿盘切削加工中,我们希望同时优化多个 conflicting(相互冲突)的目标,例如:
最小化生产成本: 通过提高材料去除率来实现。
最大化加工质量: 通过降低表面粗糙度来实现。
最大化刀具寿命: 通过减小刀具磨损来实现。
核心挑战:
目标冲突: 提高切削速度会增加材料去除率,但通常会导致表面质量下降和刀具磨损加剧。
昂贵的实验成本: 通过物理实验获取数据点成本高、周期长。
复杂的非线性关系: 切削参数(如切削速度、进给量、切削深度)与优化目标之间的关系是高度非线性的。
核心解决方案:
ELM(极限学习机): 作为一个代理模型,用来学习和预测切削参数与各个目标之间的关系。它能够用有限的实验数据快速建立高精度的非线性模型,替代昂贵的物理仿真或实验。
DE-NSGA-III(基于差分进化的第三代非支配排序遗传算法): 作为一个多目标优化器,在ELM建立的代理模型上进行搜索,寻找一系列最优的参数组合,即Pareto最优解集。DE提供了强大的全局探索能力,而NSGA-III擅长处理三个或更多目标的高维目标空间。
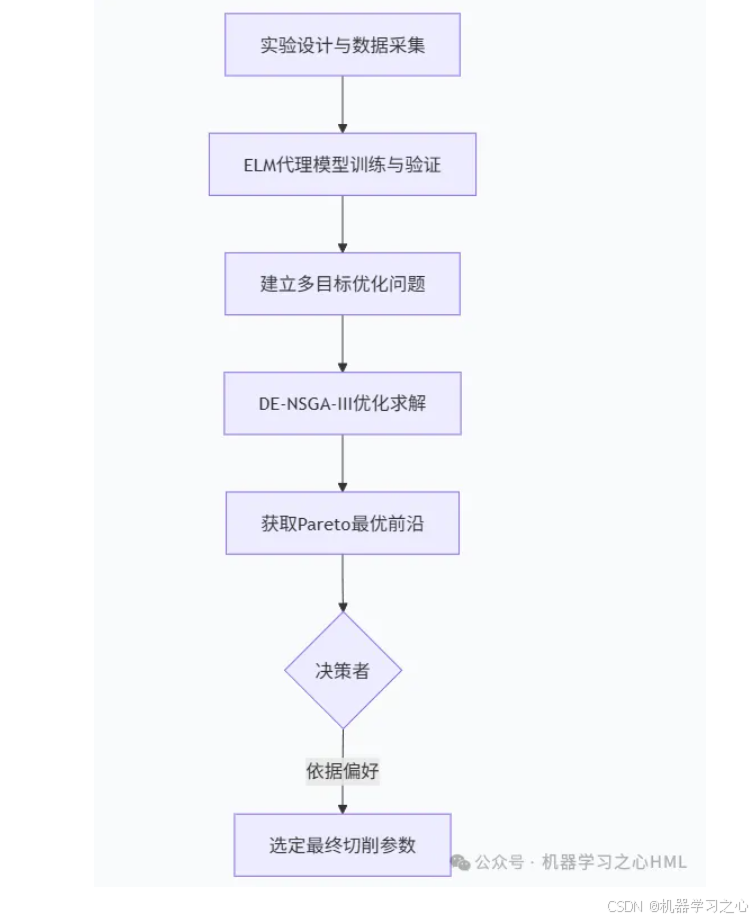
- 整体优化流程
整个方案的流程图可以概括如下:
- 详细步骤
步骤一:实验设计与数据采集
确定决策变量: 明确要优化的切削参数。
( v_c ):切削速度 (m/min)
( f ):进给量 (mm/rev)
( a_p ):切削深度 (mm)
确定优化目标: 明确要优化的性能指标。
( MRR ):材料去除率 (cm³/min),最大化
( Ra ):表面粗糙度 (μm),最小化
( T_w ):刀具磨损 (mm),最小化
设计实验: 采用如中心复合设计、拉丁超立方抽样等方法来系统地在参数空间内选取样本点,确保数据的代表性和空间填充性。
进行实验/仿真: 在选定的参数组合下进行实际切削实验或高保真有限元仿真,收集每个组合对应的 。
步骤二:ELM代理模型构建
数据预处理: 对输入(切削参数)和输出(目标响应)进行归一化处理,消除量纲影响。
模型训练:
为每个目标(MRR, Ra, Tw)分别训练一个ELM模型。
ELM的输入层有3个节点(对应 ( v_c, f, a_p )),输出层有1个节点(对应一个目标)。
随机生成输入层到隐含层的权重和偏置。
通过解析法(Moore-Penrose广义逆)计算隐含层到输出层的权重 ( \beta )。这个过程非常迅速。
模型验证: 使用留出法或交叉验证,用未参与训练的测试集数据评估ELM模型的预测精度(如使用R², RMSE)。确保模型具有足够的准确度来替代真实物理过程。
步骤三:构建多目标优化模型
将物理问题转化为标准的数学优化模型:
决策变量:
目标函数:
约束条件:
步骤四:DE-NSGA-III优化求解
初始化: 在决策变量允许的范围内,随机生成初始种群。
差分进化(DE)操作:
评估: 将父代种群和子代试验种群中的每个个体 ( \mathbf{x} ) 输入到训练好的三个ELM模型中,预测其三个目标函数值 ( (MRR, Ra, T_w) )。
NSGA-III选择:
非支配排序: 将合并的种群根据Pareto支配关系分成多个前沿等级(Front 1, Front 2, ...)。
参考点关联与选择: 这是NSGA-III的核心。预先在目标空间定义一组结构化分布的参考点。将个体与最近的参考点关联,并优先选择那些在较低前沿等级且能增加种群多样性的个体,形成新一代种群。这特别适用于三个或更多目标的情况。
迭代: 重复步骤2-4,直到满足终止条件(如达到最大迭代次数)。
步骤五:结果分析与决策
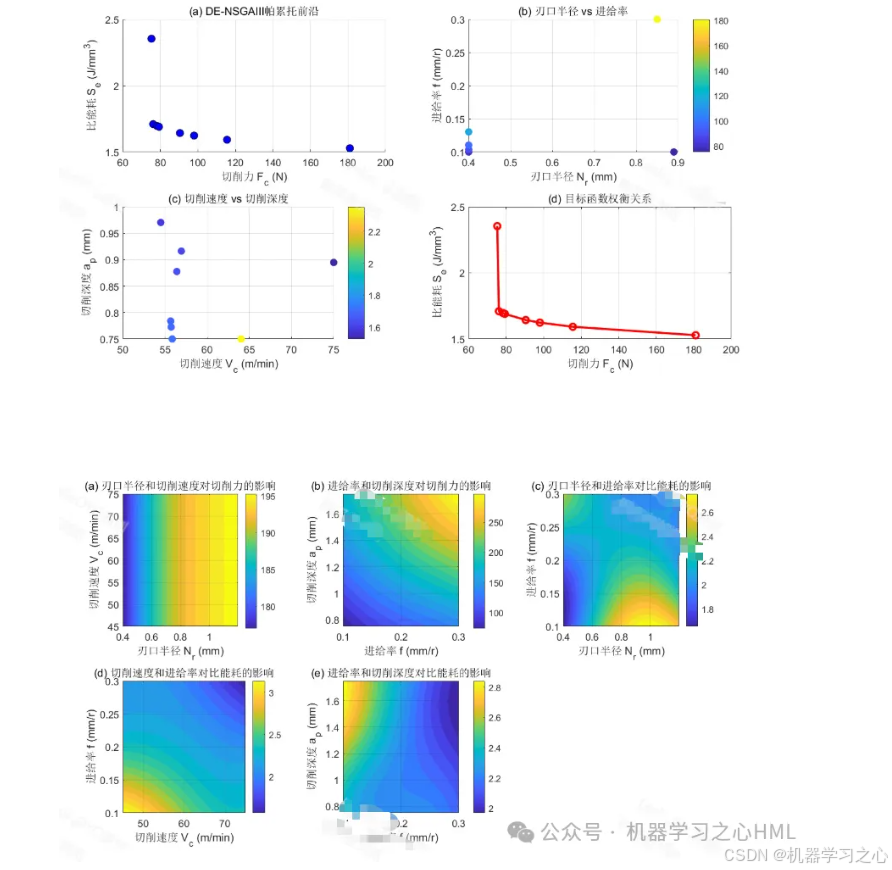
获取Pareto前沿: 算法收敛后,最终种群中的第一非支配层就是近似Pareto最优解集。这些解代表了在多个目标之间的最佳权衡。
可视化: 对于三个目标,可以绘制3D散点图来展示Pareto前沿,直观显示目标间的权衡关系。
最终决策: 将Pareto解集提供给工艺工程师。工程师可以根据实际生产需求(例如,"本次加工最看重表面质量"或"需要尽快完成生产"),从Pareto解集中挑选一个最符合当前偏好的解,其对应的切削参数即为最终优化结果。
- 方法优势
高效率: ELM的训练速度极快,避免了像神经网络那样耗时的迭代调参。DE-NSGA-III的优化过程是在快速的ELM代理模型上进行,而非昂贵的真实实验,极大降低了优化总耗时。
高精度: ELM具有良好的泛化能力,能准确拟合复杂的非线性切削过程。
强全局搜索能力: DE算子具有很强的全局探索能力,能有效避免陷入局部最优。
适用于高维目标: NSGA-III专门为处理三个及以上目标的优化问题设计,比NSGA-II在高维目标空间中表现更好。
提供丰富方案: 最终提供的是一个"最优解集",而非单一解,为决策者提供了灵活的多种选择。
- 潜在挑战与改进方向
ELM的稳定性: ELM的随机初始化可能导致模型性能有轻微波动。可以通过集成多个ELM或使用优化算法优化其输入权重来提升稳定性。
数据质量依赖: 代理模型的精度严重依赖于初始实验数据的质量和数量。精心设计实验至关重要。
算法参数调优: DE-NSGA-III本身有一些控制参数(如种群大小、F、CR),需要根据问题进行调整以获得最佳性能。