【论文阅读笔记】FedProx

[0 论文基本信息](#0 论文基本信息)
[1 内容摘要](#1 内容摘要)
[2 核心研究](#2 核心研究)
- [2.1 主要解决问题](#2.1 主要解决问题)
- [2.2 主要使用方法](#2.2 主要使用方法)
- [2.3 主要实验手段](#2.3 主要实验手段)
[3 分析与思考](#3 分析与思考)
- [3.1 评判式思考](#3.1 评判式思考)
- [3.2 创造性思考](#3.2 创造性思考)

0 论文基本信息

项目	内容
论文名称	《FEDERATED OPTIMIZATION IN HETEROGENEOUS NETWORKS》
作者	Tian Li, Anit Kumar Sahu, Manzil Zaheer, Maziar Sanjabi, Ameet Talwalkar, Virginia Smith
发表会议	【CCF-】MLSys Conference 2020
发表时间	2020年
DOI	arXiv:1812.06127v5

1 内容摘要

本文针对联邦学习中的两大关键挑战------系统异构性（设备资源不均）和统计异构性（数据非独立同分布）------提出了FedProx优化框架。FedProx是现有方法FedAvg的泛化，通过允许设备执行可变工作量并添加近端项到本地目标函数中，以稳定收敛过程。理论上，论文在非独立同分布数据下提供了收敛保证，并考虑了设备级系统约束；实践上，FedProx在多种真实联邦数据集上表现出比FedAvg更鲁棒的收敛性，在高度异构环境中平均绝对测试准确率提升了22%。

2 核心研究

2.1 主要解决问题

联邦学习在分布式环境中面临系统异构性（如设备计算能力、网络连接差异）和统计异构性（如数据分布非独立同分布）的挑战，这导致传统方法如FedAvg在收敛时可能出现不稳定或发散。FedProx旨在通过统一框架同时处理这两种异构性，避免因设备掉队或数据偏差而影响全局模型性能。

2.2 主要使用方法

FedProx的核心方法包括两个关键修改：一是允许设备根据自身系统资源执行可变工作量 （通过γ-不精确解定义），而非强制统一epoch数；二是在本地目标函数中添加近端项（如公式2： min ⁡ w h k ( w ; w t ) = F k ( w ) + μ 2 ∥ w − w t ∥ 2 \min {w} h{k}\left(w ; w^{t}\right)=F_{k}(w)+\frac{\mu}{2}\left\|w-w^{t}\right\|^{2} minwhk(w;wt)=Fk(w)+2μ∥w−wt∥2），以限制本地更新与全局模型的偏离 ，从而提高稳定性。

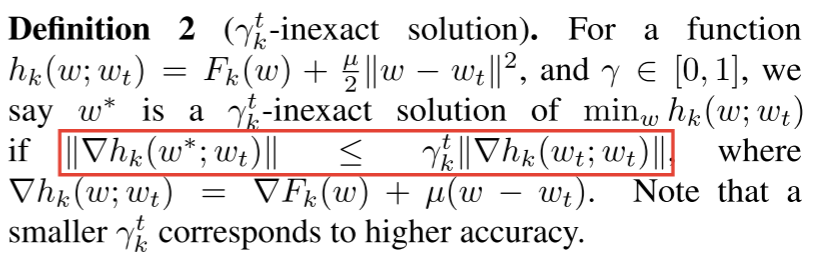
FedProx可视为FedAvg的泛化，当满足下面条件时退化为FedAvg：

(1) µ = 0 µ=0 µ=0；

(2) 本地求解器被特别选择为sgd

(3) γ γ γ为常量 (对应于本地历元的数量相同不变)

理论分析中，论文引入了B-局部差异性假设（Definition 3）来量化设备间异构性，并提供了收敛定理（Theorem 4），表明在适当参数下目标函数能单调下降。

2.3 主要实验手段

实验部分在合成数据集（Synthetic）和真实数据集（如MNIST、FEMNIST、Shakespeare、Sent140）上验证FedProx的有效性。合成数据通过参数 α α α和 β β β控制数据异构程度，模拟非独立同分布场景；真实数据集则天然具有统计异构性。实验模拟系统异构性时，随机指定部分设备执行较少epochs（如0%、50%、90%设备为掉队者），比较FedAvg（丢弃掉队者）与FedProx（纳入部分更新）的收敛行为。评估指标包括训练损失、测试准确率和差异性度量（B值）。结果通过多轮通信rounds展示，FedProx在异构设置下收敛更稳定。

3 分析与思考

3.1 评判式思考

优势	劣势
理论上有收敛保证，能处理非凸问题和异构数据。	参数 μ μ μ需要手动调整，在IID数据上可能减慢收敛速度。
实践上提高收敛稳定性和准确率，在高度异构设置平均提升22%准确率。	实验基于模拟环境，真实设备资源波动可能更复杂。
框架轻量，易集成到现有系统（如TensorFlow Federated）。	差异性度量B依赖于梯度方差，在实际中可能难以精确估计。

3.2 创造性思考

方向	内容
自动调参机制	基于启发式（如损失变化动态调整μ）或元学习优化超参数，以降低人工成本。
隐私与安全扩展	结合差分隐私或安全多方计算，增强FedProx在敏感数据下的适用性。
跨领域应用	将FedProx框架适配于边缘计算、物联网等场景，处理更广泛的异构性问题。