本文较长，建议点赞收藏。更多AI大模型应用开发学习视频及资料，在智泊AI。
本章我们开始学习大模型算法理论、网络结构及其工作原理，正式开始之前我们先关注几个问题，宏观上理解大模型的概貌。
1.大模型到底大在哪里？
大模型的"大"本质是"规模法则"（Scaling Laws）驱动下的系统性扩张：当模型、数据、算力同步增大时，模型能力会以可预测的方式提升，甚至涌现出小模型不具备的能力（如推理、泛化、指令遵循）。大模型的"大"并不仅仅指参数数量多，而是多维度的"规模扩展"（Scaling），主要包括：参数规模大、训练数据量规模大、计算量大、上下文长度等。
1）参数规模（Model Size）大：知识容量与记忆能力+泛化能力+涌现能力
DeepSeek爆火之后，经常听到"参数"、8b、14b、32b、70b和671b...，"GPT-3有1750亿参数""DeepSeek-V3含6710亿参数"，GPT-4、Gemini Ultra、Qwen3-Max万亿规模"参数"...这些天文数字具体是啥意思？
参数就像是模型的"脑细胞"（神经元及神经网络规模）。参数越多，模型的"大脑"容量就越大，能够存储和记忆更多的信息。在训练过程中，模型从海量文本中学习到的语法知识、事实知识、推理模式等，都被编码存储在这些参数中。
参数量越大，它能记住和理解的细节就越多、越复杂。巨大的参数量使得模型在遇到未曾见过的输入时，也能通过组合其学到的海量模式，给出合理、流畅的回应。它不再是简单的"死记硬背"，而是具备了强大的举一反三的能力。涌现能力是大模型最神奇的特性，当模型规模（包括参数量、数据量、计算量）超过某个临界点时，模型会表现出在较小模型中不存在或极不明显的能力。
2）训练数据量大（Data Scale）：训练语料的 token 数量，从几十亿 → 数万亿 tokens（如 GPT-4 训练约 13T tokens）。
3）计算量大（Compute Scale）：训练所需的 FLOPs（总浮点运算次数）从 petaFLOP-days → exaFLOP-days（GPT-4 约 2.15e25 FLOPs）。FLOP/s 是什么？表示计算速度，即每秒能做多少次浮点运算。1 petaFLOP/s = 10的15次幂/秒，1 exaFLOP/s = 10的18次幂/秒
💡 类比：FLOPs 是"总共要搬多少块砖"，FLOP/s 是"每秒能搬多少块砖"。
"FLOP-days" 是什么意思？这是一个将计算总量与时间结合的单位 ，用于衡量训练所需的总计算量。定义：
1 petaFLOP-day = 以 1 petaFLOP/s 的速度 持续计算 1 天 所完成的总运算量。
4）上下文长度（Context Length）：单次输入能处理的 token 数，从 512 → 32K（Claude）、128K（Grok-2）、1M+（Gemini 1.5）、1M+(Qwen3-Max)。
2.参数规模与哪些因素有关？
2.1 什么是大模型参数？
在神经网络中，参数是模型在训练过程中需要从数据中学习的内部变量。您可以把它想象成一个极其复杂的数学函数（模型）中的 * 可调节的旋钮或权重*。每一个参数都负责捕捉数据中的某种细微模式，参数（Parameters） 是指模型在训练过程中需要学习的权重（Weights）和偏置（Biases），具体包括：
1）权重：连接神经元之间的数值（如全连接层、注意力层的矩阵）。
2）偏置：每个神经元的附加偏移量。
示例：一个简单的全连接层（输入维度=100，输出维度=200）的参数量为：100（输入） × 200（输出） + 200（偏置） = 20,200。
2.2 大模型参数规模与哪些因素有关？
模型的参数可理解为其可调节的"神经元"数量，模型参数规模越大理论上学习和存储信息的能力就越强。大模型的参数规模并非随意设定，任务越复杂（如通用对话、代码生成、科学推理），所需模型容量越大。参数规模由以下因素共同决定：
1）模型架构：模型架构（层数、维度）直接决定了参数量的大小和利用效率。
-
核心网络结构 ：目前主流大模型基于Transformer架构 。其参数主要来自注意力机制 （如自注意力中的查询、键、值矩阵）和前馈神经网络的权重矩阵。
稠密模型（Dense）：所有参数参与每次计算（如 Llama 3 405B）。
稀疏模型（Sparse / MoE）：仅部分参数激活（如 Mixtral 8x7B、Gemini Ultra）。MoE 可在不显著增加推理成本的前提下"做大"总参数。
-
模型架构复杂度：表示能力与抽象层次，模型结构设计（如 MoE、多模态融合），混合专家（MoE）、视觉-语言对齐、工具调用能力等。为应对参数膨胀带来的计算成本，混合专家模型 (Mixture of Experts)成为重要方向。MoE模型拥有总量巨大的参数（如DeepSeek-V3总参数量6710亿），但通过稀疏激活机制，在处理单个任务时仅调用其中一小部分"专家"（如DeepSeek-V3每次推理仅激活约670亿参数），实现了在保持强大能力的同时控制计算开销。
-
简单来说，你可以把模型想象成一个建筑：层数（深度）和每层的房间数（宽度）直接决定了需要多少"砖块"（参数）。
2）训练数据是燃料：模型参数需要海量数据来学习和调整。
- 数据规模vs模型参数规模：参数量的增加需要与之匹配的大规模训练数据，以避免模型"消化不良"（训练不足）。模型参数需与数据量匹配。数据太少 → 过拟合；模型太小 → 欠拟合。另外，数据质量也很重要，高质量、多样化的数据能更有效地驱动参数学习到有用的知识和规律。
- 训练数据规模：研究表明在固定计算预算下，存在一个最优模型大小与数据量的配比（如 Chinchilla Scaling Law）。Chinchilla 定律建议：理想情况下，数据量应是参数量的 20 倍左右（以 token 计）。例如，Qwen3-Max的训练数据就达到了36万亿token，模型参数规模1万亿多。
3）算力成本是门槛：参数规模直接受限于可用算力、电力、资金。训练和运行大模型消耗巨大。
- 训练算力：训练一个671B参数的DeepSeek-R1模型需要消耗约3.2M的GPU小时。训练 1 万亿参数模型需数千张 H100 GPU 运行数月，成本超数亿美元
- 推理成本：即使在采用MoE等技术优化后，大模型的部署和推理仍需昂贵的硬件支持
2.3 如何计算大模型的参数规模？大模型的网络结构及工作原理
既然我们了解到模型参数规模核心依赖模型网络架构，我们以GPT3的网络结构为例，Transformer中参数主要来自嵌入层、Transformer层（包括自注意力和前馈网络）和输出层。模型的"蓝图"决定了需要多少参数来构建它。Transformer层数：模型有多"深"。每一层都包含一系列参数。层数越多，参数自然越多。隐藏层维度：模型有多"宽"。这是模型内部表示向量的尺寸。维度越大，每个层内的参数就越多（因为矩阵更大）。注意力头数和维度：Transformer核心------自注意力机制中，头数越多、每个头的维度越大，对应的参数也就越多。词汇表大小：输入和输出层的维度通常与词汇表大小相关。词汇表越大，嵌入层的参数就越多。
1）V: vocab_size (词汇表大小)
2）H: hidden_size (隐藏层维度，即d_model)
3）L: num_layers (Transformer层数)
4）A: num_attention_heads (注意力头数)
5）F: feed_forward_size (前馈网络内部维度，通常为4*H)
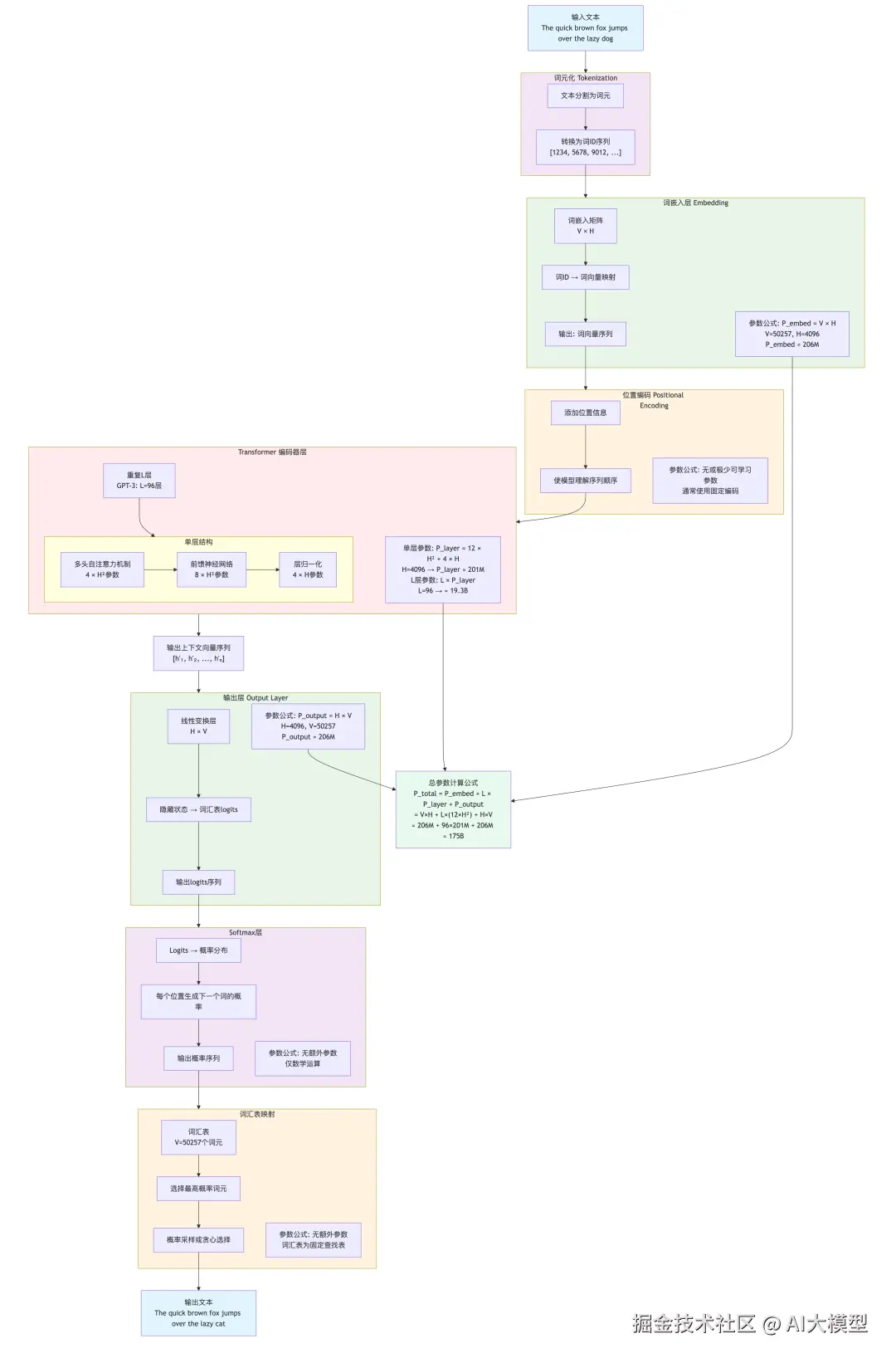在标准Transformer中，前馈网络内部维度通常为4H，所以F=4H。参数计算：
1）词嵌入层参数：P_embed = V * H
2）位置编码参数 (黄色区域)：通常使用固定正弦/余弦编码，无可学习参数。某些变体使用可学习的位置编码，参数数量为 max_seq_len × H（可以忽略）。
3）输出层：通常与嵌入层共享权重，如果不共享，则为P_output = H * V
4）单个Transformer层：单个Transformer层的参数大约为12*H^2
- 自注意力部分：Q、K、V、投影矩阵：3 * (H * H) ，输出投影矩阵：H * H，所以自注意力部分总共4*H^2
- 前馈网络部分：第一个线性层：H * (4H) = 4H^2，第二个线性层：(4H) * H = 4H^2，所以前馈网络部分总共8*H^2
- 层归一化：每个层归一化有两个可学习参数（缩放和偏移），每个参数大小为H。通常每层有两个层归一化（自注意力后和FFN后），所以是4*H。但是与H^2相比很小，通常忽略。
- 计算：单个Transformer层的参数大约为12*H^2。
5）L层Transformer总参数P_transformer = L*P_layer，Transformer层数 96。
6）总参数 = 嵌入层 + 输出层 + L * (12*H^2) = V×H + L×(12×H²) + H×V = 2×(V×H) + 12×L×H²
案例：GPT-3 175B 参数计算实例，参数：V = 50,257，H = 12,288 (GPT-3实际使用)，L = 96。 计算过程：
P_embed = 50,257 × 12,288 ≈ 617M P_layer = 12 × 12,288² ≈ 12 × 151M ≈ 1.81B P_transformer = 96 × 1.81B ≈ 174B P_output = 12,288 × 50,257 ≈ 617M
P_total = 617M + 174B + 617M ≈ 175B
2.4 模型训练反向传播过程
本节补一下上一篇工程师学AI之第五篇：从微积分梯度及链式法则，到神经网络学习优化过程，神经网络训练过程前向传播及反向传播过程如何调整模型权重参数？加深对神经网络工作机制的理解。
1）前向传播：
输入x→[w₁]→h₁→[w₂]→h₂→[w₃]→y→与目标target比较→Loss
h₁=f₁(x, w₁) #第1层：h₁是x和w₁的函数
h₂=f₂(h₁, w₂) #第2层：h₂是h₁和w₂的函数h₂=f₂(f₁(x, w₁), w₂)
y=f₃(h₂, w₃) #第3层：y是h₂和w₃的函数y=f₃(f₂(f₁(x,w₁),w₂), w₃)
Loss = L(y, target) # 损失：损失函数L是模型输出y和真实标签target的函数Loss=L(f₃(f₂(f₁(x, w₁), w₂), w₃), target)
2）反向传播：损失函数如何通过链式法则影响到每一层的权重，梯度 ∂L/∂w₁ ← ∂L/∂h₁ ← ∂L/∂h₂ ← ∂L/∂y (误差信号反向传播)
∂Loss/∂w₃ = ∂L/∂y · ∂y/∂w₃
∂Loss/∂w₂ = ∂L/∂y · ∂y/∂h₂ · ∂h₂/∂w₂
∂Loss/∂w₁ = ∂L/∂y · ∂y/∂h₂ · ∂h₂/∂h₁ · ∂h₁/∂w₁
3）更新权重：根据学习率lr和损失函数更新权重
w3 = w3 - lr * ∂Loss/∂w₃ #grad_w3
w2 = w2 - lr * ∂Loss/∂w₂ #grad_w2
w1 = w1 - lr * ∂Loss/∂w₁ #grad_w1
4）案例：假设一个简单网络：
x = 2, w₁ = 0.5, w₂ = 1.2, w₃ = 0.8
h₁ = w₁·x = 1.0
h₂ = w₂·h₁ = 1.2
y = w₃·h₂ = 0.96
target = 1.0, Loss = (y - target)² = 0.0016
#反向传播计算：
∂L/∂y=2(y-target)=-0.08
∂L/∂w₃=∂L/∂y·h₂=-0.08×1.2=-0.096
∂L/∂w₂=∂L/∂y·w₃·h₁=-0.08×0.8×1.0=-0.064
∂L/∂w₁=∂L/∂y·w₃·w₂·x =-0.08×0.8×1.2×2=-0.1536
#权重更新（学习率 lr=0.1）：根据反向传播计算的偏导数更新权重
w₃'=0.8-0.1×(-0.096)=0.8096
w₂'=1.2-0.1×(-0.064)=1.2064
w₁'=0.5-0.1×(-0.1536)=0.51536
3.大模型参数规模有没有极限？
关于参数规模是否有极限，目前并没有一个确切的数字天花板，但确实面临着多方面的挑战和新的发展趋势：
1）规模法则的指导与挑战 ：研究发现，模型性能随规模增长遵循一定的规模法则 (Scaling Laws)，但这种增长关系可能并非一成不变。
- 收益递减 ：根据断裂式规模法则 (Broken Neural Scaling Laws) ，模型性能随规模增长可能呈现分段式提升 ，在某些阶段会出现收益递减的拐点。Chinchilla法则的启示 ：研究表明，在计算预算固定时，盲目增加参数而非同步增加训练数据，并非最优解。模型参数与训练数据需要平衡分配。例如：从 100B → 500B 提升显著，但从 1T → 2T 可能只有边际改进。
2）硬件物理极限与成本约束：巨大的算力消耗和资金成本，从现实层面限制了参数规模的无限增长，商业回报能否覆盖成本，是决定"还能不能更大"的关键。
芯片互联带宽：参数需在 GPU 间频繁通信，带宽瓶颈。
内存墙（Memory Wall）：单卡显存有限（如 H100 80GB），超大模型需模型并行，通信开销剧增。
能耗限制：训练 GPT-4 耗电约 1300 MWh，相当于数百家庭年用电量 。
成本呈指数增长：GPT-3（175B）训练成本 ≈ <math xmlns="http://www.w3.org/1998/Math/MathML"> 460 万， G P T − 4 （ 1.5 T M o E ） ≈ 460 万，GPT-4（1.5T MoE）≈ </math>460万，GPT−4（1.5TMoE）≈7800 万 -- $2 亿美元。
3）超越参数膨胀的新路径：探索重点正从单纯堆砌参数，转向更高效的技术路径。
- 架构创新 ：如前所述的MoE架构 ，以及多头潜在注意力 (MLA) 等新技术，旨在不显著增加计算代价的前提下提升模型能力。
- 推理时计算 ：另一种思路是增加模型在推理阶段的"思考"量，例如通过更复杂的思维链 (Chain-of-Thought) 或搜索过程来提升任务表现，这被视为一种"推理时的规模扩展"。
4） 数据可获性：需要"喂养"模型的知识量，根据Chinchilla定律，模型的参数量需要与训练数据的量级相匹配。参数是"容器"，数据是"粮食"。一个巨大的模型（大容器）需要海量的高质量数据（足够多的粮食）来"填满"，才能充分发挥其潜力。如果用一个万亿参数的模型去训练一个只有十亿token的数据集，它极易过拟合（只记住了训练数据，而没有泛化能力），这是巨大的资源浪费。因此，在确定参数量时，必须考虑：我们能否获得足够多、高质量的数据来有效训练这个模型？数据规模决定了参数规模的有效上限。
5）算法与工程优化
先进的算法和工程技术可以让我们在相同的参数量下获得更好的性能 ，或者在相同的性能下使用更少的参数。更高效的架构：如混合专家模型，它通过动态激活网络中的一部分参数来在总参数量巨大的情况下，大幅减少实际计算量。模型压缩与量化：在部署时，通过技术手段减少每个参数占用的比特数（如从32位浮点数降到8位整数），但这不改变参数的数量，只改变模型的总大小。
4.如何估算硬件资源？
根据大模型的参数规模来配置硬件资源是一个系统工程，需要综合考虑训练和推理两个阶段。这里我们主要讨论训练，因为训练对硬件的要求更高。推理阶段可以根据训练阶段的配置进行适当缩减。
4.1训练阶段
训练大模型时，硬件资源配置的核心是能够容纳模型并高效地进行计算。主要考虑以下因素：
1）内存（GPU显存）：内存是首要瓶颈，必须能够存储模型参数、优化器状态、激活值、梯度以及临时缓冲区。训练时的总内存占用包括四个主要部分：
总内存 ≈ 模型参数 + 优化器状态 + 梯度 + 激活值
单精度浮点数：FP32/BF32 ：4× 参数量 bytes，用于训练场景
半精度浮点数：FP16/BF16 ：2 × 参数量 bytes，训练和部分推理场景
INT8量化：1 × 参数量 bytes，8位整数量化，推理常用
INT4量化：0.5 × 参数量 bytes，4位整数量化，轻量级推理
2）计算能力（FLOPs）：硬件需要提供足够的计算能力，以便在合理的时间内完成训练。
3）通信带宽：在多卡或多节点训练时，卡间或节点间的通信带宽至关重要。
通过前面的学习，你已经了解了模型训练的本质，是寻找最合适的参数组合。没有"最好"的配置，只有"最适合"的配置。需要根据你的具体需求、预算和时间约束来平衡这些因素。
案例：参考阿里云ACP大模型培训资料，以qwen2.5-1.5b-instruct 为例，粗略看下从零训练一个模型的时间和硬件需求。 为了微调大模型，你需要估算显存要求，1.5B参数占用内存（假设按全精度 FP32 ，单参数占用4字节）：
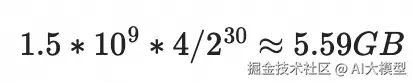
一般对模型进行训练时，大概需要模型参数内存的7~8倍，也就是约45GB的显存。
4.2推理阶段 推理阶段的内存需求相对简单：推理总内存 ≈ 模型参数 + KV缓存，推理阶段可以根据训练阶段的配置，以及预估的并发用户量进行适当缩减。
1) 模型参数内存
FP16/BF16 ：2 × 参数量 bytes
INT8量化：1 × 参数量 bytes
INT4量化：0.5 × 参数量 bytes
2) KV缓存内存：对于自回归生成任务，需要缓存Key和Value。
python
KV缓存 ≈ 2 × 层数 × 隐藏维度 × 注意力头数 × 序列长度 × 批次大小 × 2 bytes因此，推理时单卡总内存估算：总内存 ≈ P × (2-4) + KV缓存。
学习资源推荐
如果你想更深入地学习大模型，以下是一些非常有价值的学习资源，这些资源将帮助你从不同角度学习大模型，提升你的实践能力。
本文较长，建议点赞收藏。更多AI大模型应用开发学习视频及资料，在智泊AI。