代码随想录 70.爬楼梯

思路：爬到第一层有1种方法，爬到第二层有2种方法。那么第一层楼梯再跨两步就到第三层，第二层楼梯再跨一步就到第三层。所以到第三层楼梯的状态可以由第二层楼梯和第一层楼梯的状态推导出来，所以可以动态规划。

动规五部曲：

本题需要一个一维数组来记录不同楼层的状态。

1.确定dp数组及其下标的含义：

dp[i]：爬到第i层楼梯，有dp[i]种方法。

2.确定递推公式：

如何可以推出dp[i]呢？从dp[i]的定义来看，dp[i]可以有两个方向推出来。

（1）首先是dp[i - 1]，上i - 1层楼梯，有dp[i - 1]种方法，那么下一步上1个台阶就到dp[i]了。

（2）还有dp[i - 2]，上i - 2层楼梯，有dp[i - 2]种方法，那么下一步上2个台阶就到dp[i]了。

因此dp[i]就是dp[i - 1]和dp[i - 2]的和。

dp[i] = dp[i - 1] + dp[i - 2]。

在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。这体现出确定dp数组及其下标含义的重要性。

3.dp数组如何初始化：

dp[i]的含义是，爬到第i层楼梯，有dp[i]种方法。

那么i为0时，dp[i]应该为多少？在本题中，i为0时，dp[0] = 0 或 dp[0] = 1有争议。这是因为第0层台阶，既可以解释为爬到第0层也是一种方法，所以dp[0] = 1；也可以解释为dp[0]时楼层是0，直接站在楼顶上了没有移动，所以dp[0] = 1。在本题中，n是一个正整数，所以题目中没有n为0的情况。所以本题不需要讨论dp[0]的初始化。而本题中，dp[1] = 1，dp[2] = 2是没有争议的。所以本题不考虑dp[0]如何初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。

4.确定遍历顺序：

从递推公式 dp[i] = dp[i - 1] + dp[i - 2]可以得出，遍历顺序是从前向后的。

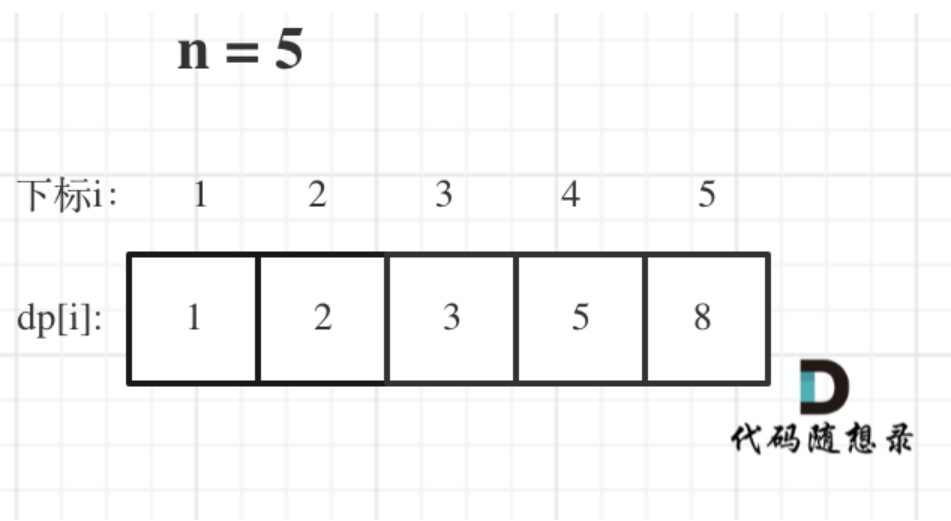
5.举例推导dp数组：

当n为5时，dp数组如下所示。

附代码：

java 复制代码

class Solution {
    public int climbStairs(int n) {
        if(n <= 2) return n;
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3;i <= n;i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

java 复制代码

//用变量记录代替数组
class Solution {
    public int climbStairs(int n) {
        if(n <= 2) return n;
        int a = 1,b = 2,sum = 0;
        for(int i = 3;i <= n;i++){
            sum = a + b;
            a = b;
            b = sum;
        }
        return b;
    }
}