商务数据分析与可视化

商务数据分析与可视化

大数据可视化概述

视觉感知

视觉感知---格式塔（(Gestalt)视觉原理

• 格式塔视觉原理

  • 帮助理解个体如何通过视觉认识周围世界的规则
  • 解释了在呈现图形元素时人类有组织感知的模式和对象

• 一个基本点

  • 人类的视觉是整体的

• 两个基本假设

  • 捆绑假设:每个复合体都由基本内容或片段组成
  • 关联假设:如果任意对象或场景频繁与另一对象或场景一同出现，那么人们通常倾向于在其中一个对象或场景出现时，召唤另一个

• 六个原则

  1. 相似原侧(Similarity Principle)
  2. 临近原则(Proximity Principle)
  3. 连续原则(Continuity Principlel)
  4. 闭合原则(Closure Principle)
  5. 图形与背景关系法则(Figure-Ground Articulation)
  6. 连接原则(Connectedness Principle)

---

第一章 数据分析概论

混淆矩阵

真实\预测	正类	负类
正类	TP（真阳性）	FN（假阴性）
负类	FP（假阳性）	TN（真阴性）

1. 准确度（整体分类正确率）：(TP + TN) / (TP + TN + FP + FN)
2. 精确度（预测正类的可靠性）：TP / (TP + FP)
3. 召回率（找全正类的能力）：TP / (TP + FN)
4. F1分数（平衡精确率和召回率）：2×(精确度×召回率) / (精确度+召回率)

方差与偏差

维度	高偏差（欠拟合）	高方差（过拟合）
定义	模型预测均值与真实值差距大，拟合能力弱	模型在不同训练集上预测结果波动大，稳定性差
原因	模型过于简单（如线性模型拟合非线性数据）	模型过于复杂（如深度过深的决策树），对噪声敏感
表现	训练集和测试集精度都低	训练集精度高，测试集精度低
典型案例	用线性回归预测复杂曲线的房价走势	用单棵深度决策树直接拟合含噪声的图像分类数据
解决方向	增加模型复杂度（如用多项式特征、换复杂模型）	降低模型复杂度（如正则化、减少特征、集成学习）

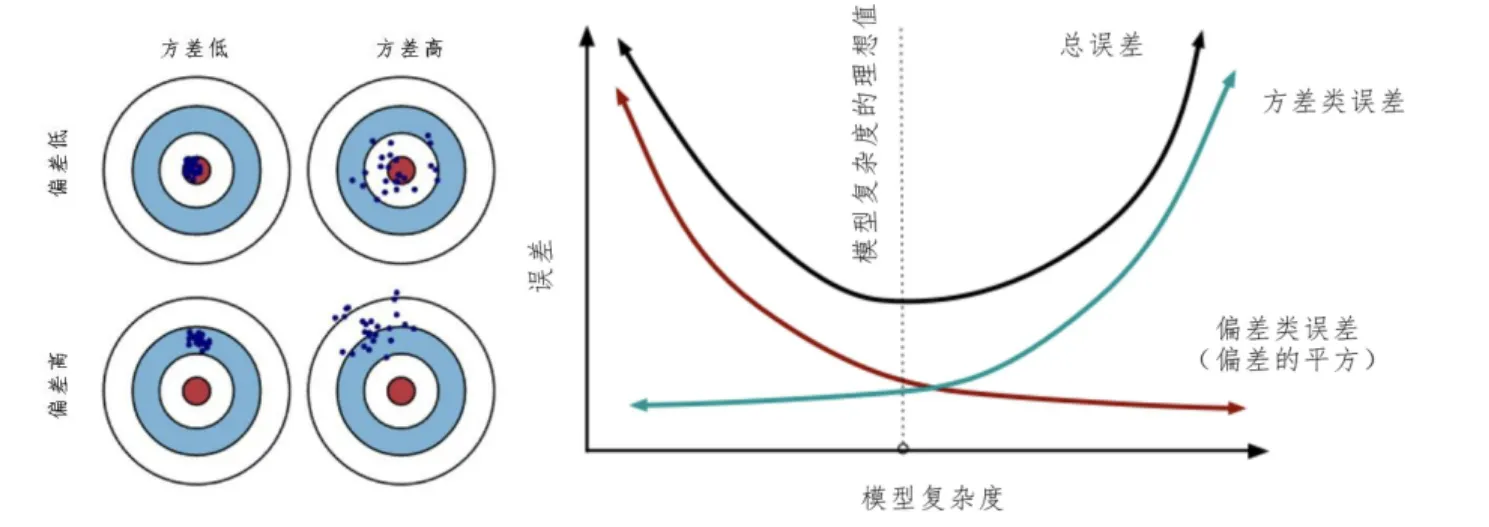
正常学习曲线

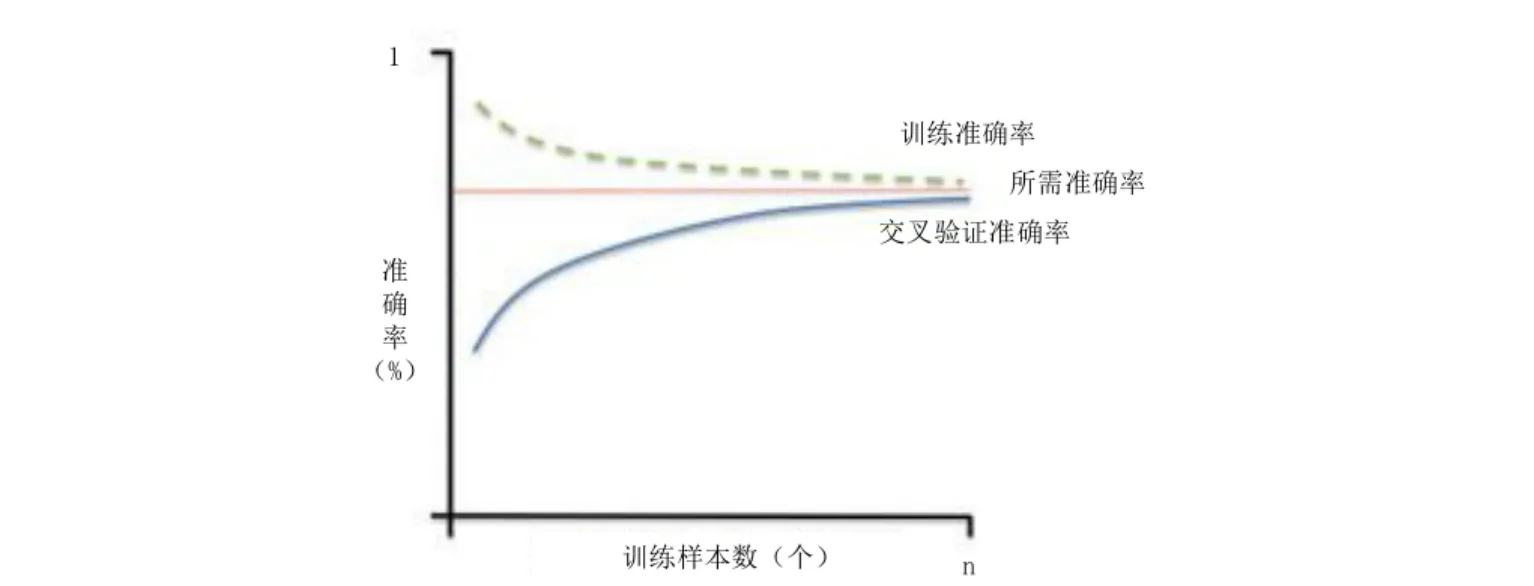
高方差学习曲线

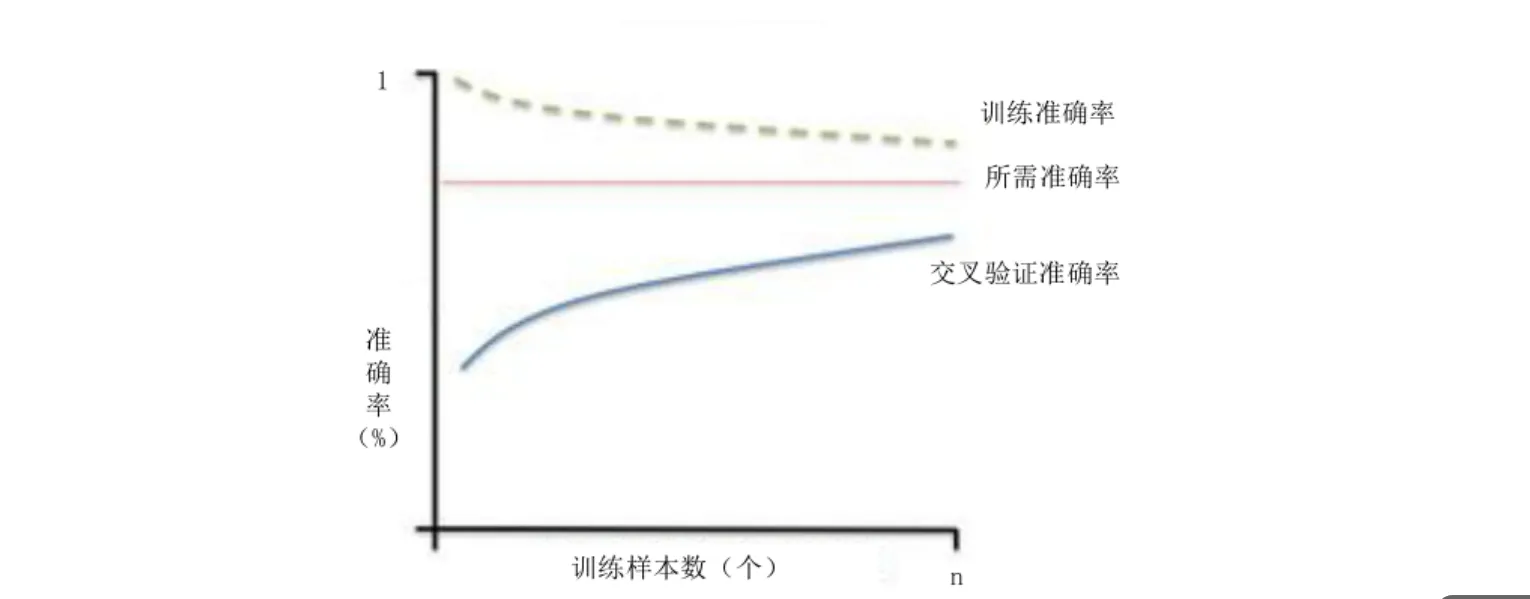
高偏差学习曲线

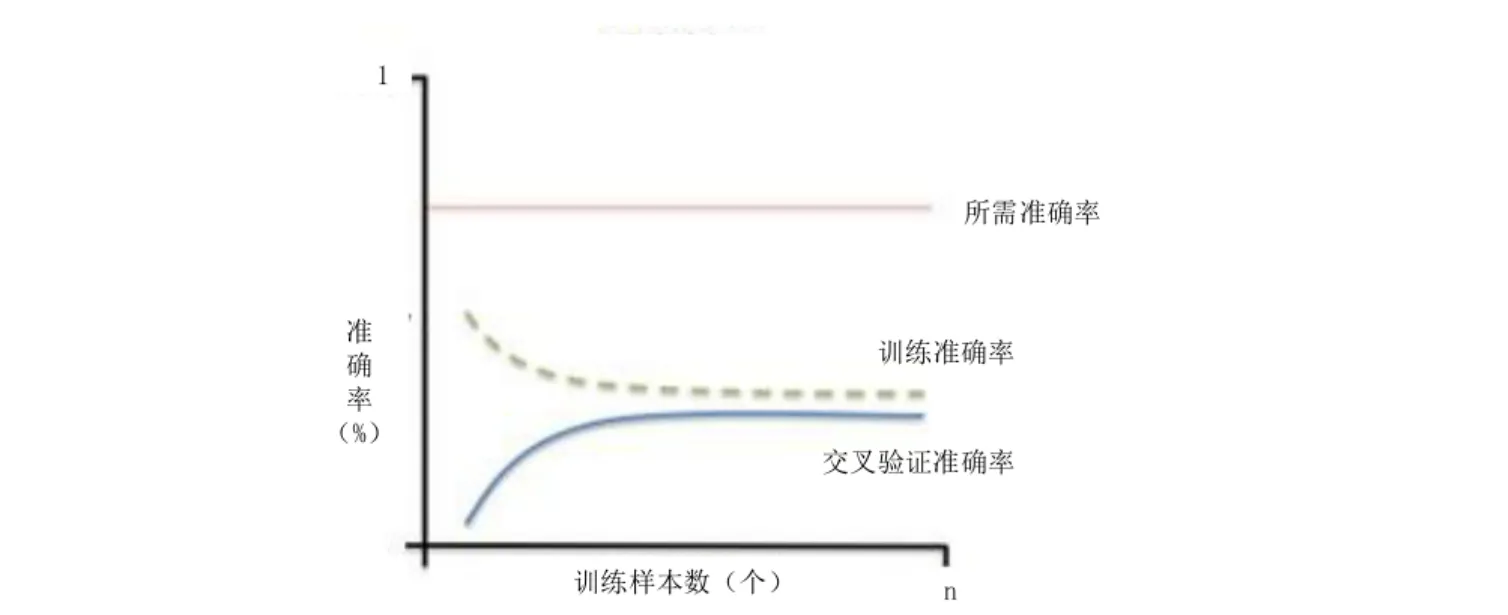
Gartner分析学价值扶梯模型

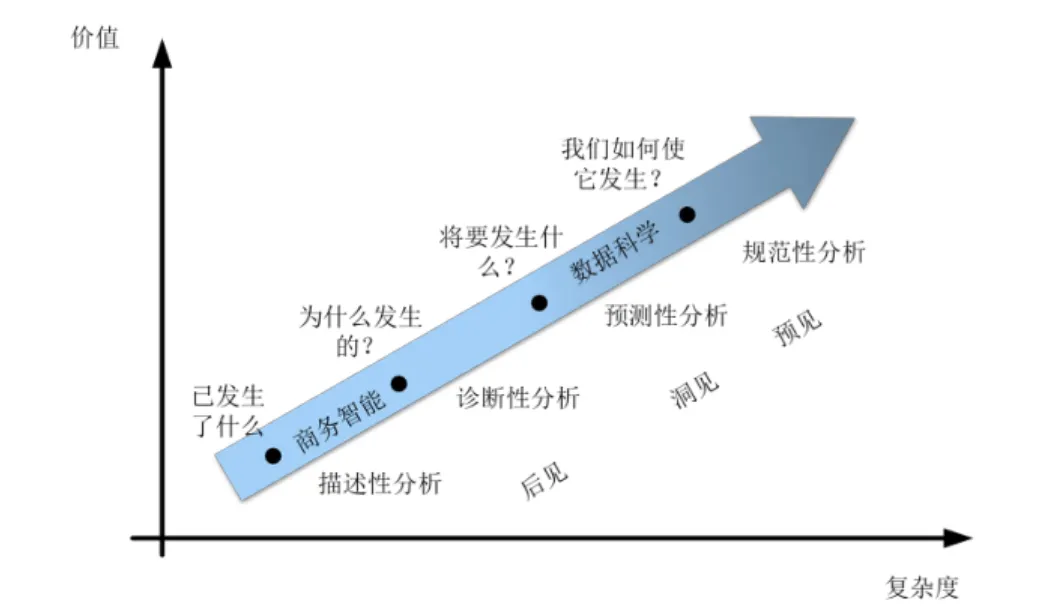
数据分析的基本类型

有监督学习算法和无监督学习算法

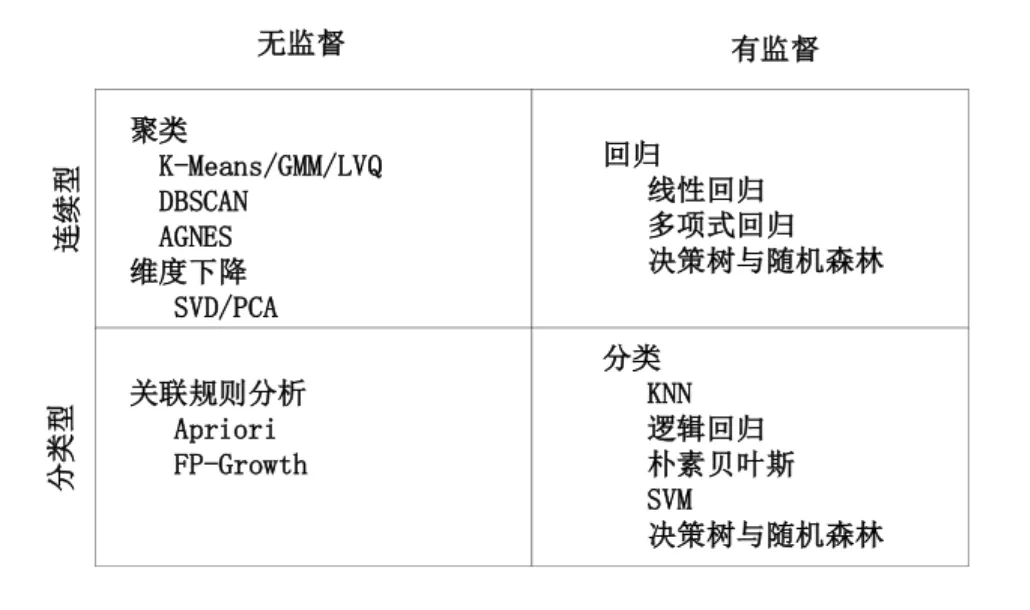
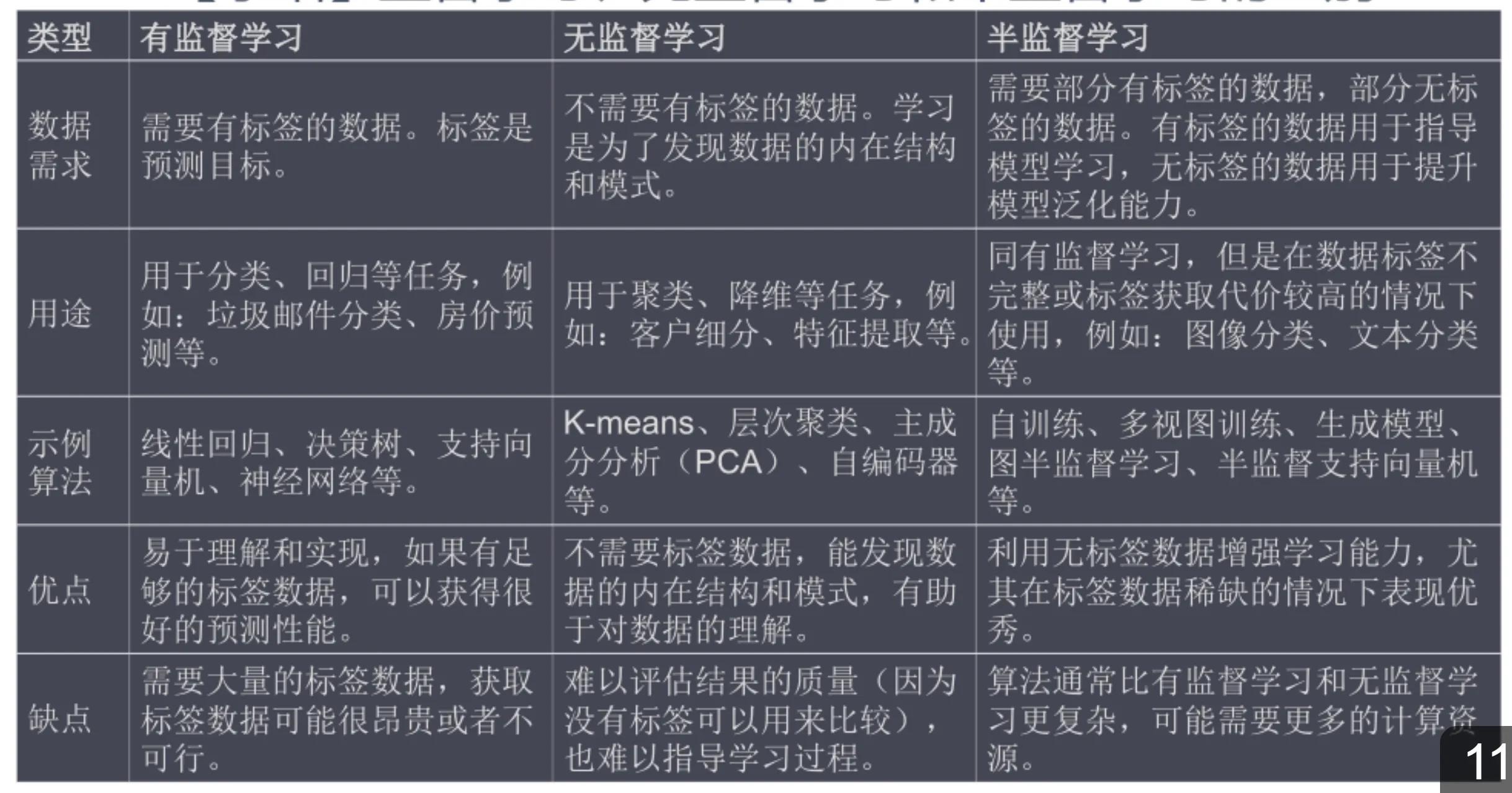
数据分析主要流程

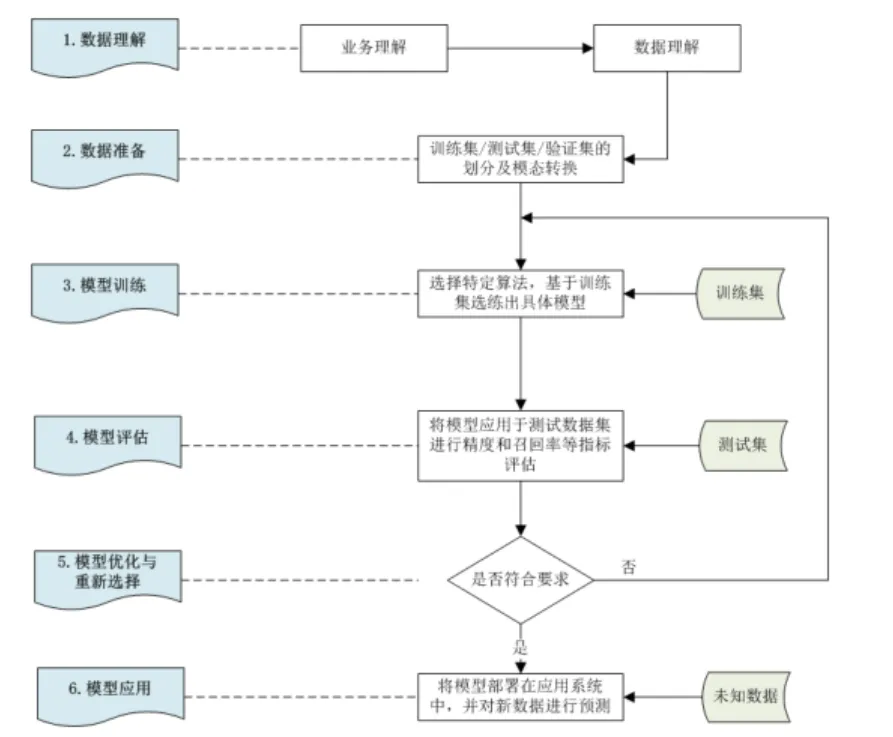
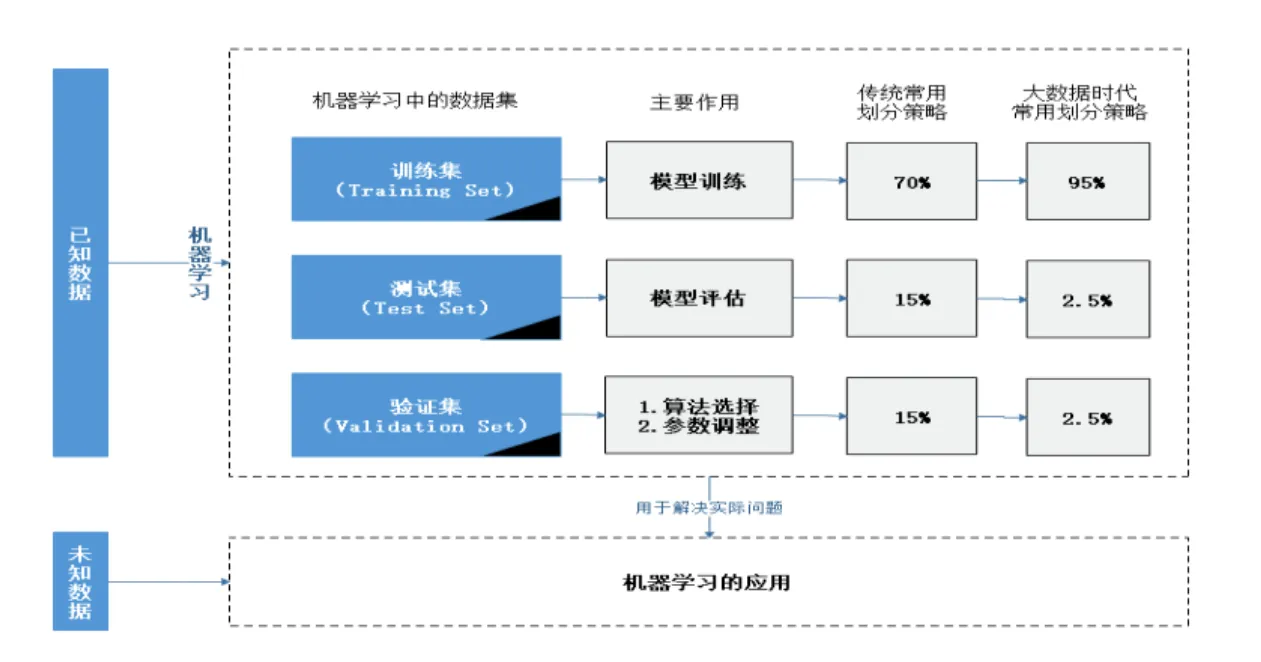
机器学习中的数据划分

---

第二章 关联规则分析

项以及K-项集

支持度(Support)

"支持度(Support)"是指项集出现的频繁程度

Support({A,B})=P(AB)=A和B同时被购买的次数总购买次数\text{Support}(\{\text{A,B}\}) = \text{P(AB)} = \frac{\text{A和B同时被购买的次数}}{\text{总购买次数}}Support({A,B})=P(AB)=总购买次数A和B同时被购买的次数

支持度越高，则说明A和B这两个商品一起出现的概率越大

置信度(Confidence)

"置信度(Confidence)"是指在A发生的同时发生B的概率

Confidence({A}→{B})=P(B∣A)=support({A,B})support({A})\text{Confidence}(\{ \text{A} \} \rightarrow \{ \text{B} \}) = \text{P}(\text{B} | \text{A}) = \frac{\text{support}(\{\text{A,B}\})}{\text{support}(\{\text{A}\})}Confidence({A}→{B})=P(B∣A)=support({A})support({A,B})

"最小置信度"是指人为规定的有实际意义的阈值，表示关联规则最低的可靠程度。

提升度(Lift)

提升度(Lift)是指A的出现的对B的出现概率的提升程度

Lift({A}→{B})=P(B∣A)P(B)=Confidence({A}→{B})Support({B})\text{Lift}(\{ \text{A} \} \rightarrow \{ \text{B} \}) = \frac{\text{P}(\text{B}|\text{A})}{\text{P}(\text{B})} = \frac{\text{Confidence}(\{ \text{A} \} \rightarrow \{ B \})}{\text{Support}(\{ \text{B} \})}Lift({A}→{B})=P(B)P(B∣A)=Support({B})Confidence({A}→{B})

• 若 Lift>1\text{Lift} > 1Lift>1，说明购买A会提高购买B的概率，A和B正相关；
• 若 Lift=1\text{Lift} = 1Lift=1，说明A和B相互独立，购买A不影响购买B的概率；
• 若 Lift<1\text{Lift} < 1Lift<1，说明购买A会降低购买B的概率，A和B负相关。

关联规则与强关联规则

• 关联规则 ：是以itemset1→itemset2的形式，表示在itemset1发生时也会发生itemset2
  的关系。例如，{B}→{C,E}就是一条关联规则，表示在B出现的同时也会出现C和E。
• 强关联规则：是指满足最小支持度和最小置信度的关联规则例如，关联规则{B}→{C,E}就是一条强关联规则，它符合最小支持度2和最小置信度50%。

第三章 回归分析

回归分析的主要类型

分类依据	特征	类型
自变量	只有一个，且最高幂次为1	简单线性回归
	最高幂次大于1	多项式回归
	多个	多元回归
因变量	计数型	泊松回归
	真/假二分类型	逻辑回归
正则化（惩罚）方式	L1正则化	Lasso回归
	L2正则化	岭回归（Ridge Regression）

观察值、预测值和残差

ei=yi−y^i{e_i = y_i - \hat{y}_i}ei=yi−y^i

评价方法---判定系数

R2=∑(y^i−yˉ)2∑(yi−yˉ)2=1−∑(yi−y^i)2∑(yi−yˉ)2{R^{2}=\frac{\sum(\hat{y}{i}-\bar{y})^{2}}{\sum(y{i}-\bar{y})^{2}}=1-\frac{\sum(y_{i}-\hat{y}{i})^{2}}{\sum(y{i}-\bar{y})^{2}}}R2=∑(yi−yˉ)2∑(y^i−yˉ)2=1−∑(yi−yˉ)2∑(yi−y^i)2

• R2越接近于1，回归线的拟合程度越好
• R2越接近于0，回归线的拟合程度越差

评价方法一均方误差(Mean Square Error,MSE)

MSE=Σ(yi−y^i)2dfMSE{MSE=\frac{\Sigma(y_i-\hat{y}i)^2}{df{MSE}}}MSE=dfMSEΣ(yi−y^i)2

p为自变量的个数；dfMSE为MSE的自由度，dfMSE=n-p-1

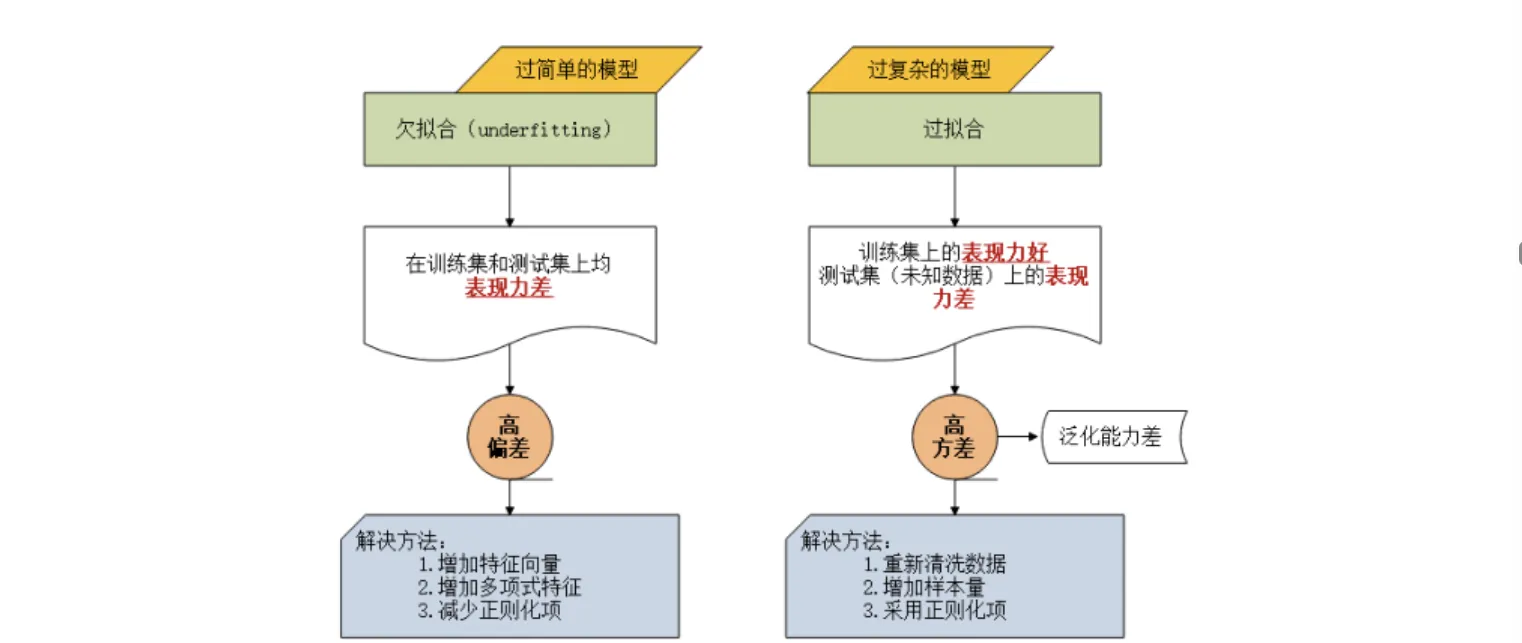
过拟合与欠拟合

四种常用的离群点识别方法

1. 箱线图
2. 四分位距
3. Z-Source
4. 聚类

L1正则

L1 正则化（L1 Regularization）是回归分析中用于防止模型过拟合、简化模型 的一种正则化技术，核心是在损失函数中加入模型参数绝对值之和作为惩罚项。

LL1=∑i=1n(yi−y^i)2+λ∑j=1k∣βj∣{L_{\mathrm{L}1}=\sum_{i=1}^n(y_i-\hat{y}i)^2+\lambda\sum{j=1}^k|\beta_j|}LL1=∑i=1n(yi−y^i)2+λ∑j=1k∣βj∣

L2正则

L2 正则化（L2 Regularization）是回归分析中用于防止模型过拟合 的正则化技术，核心是在损失函数中加入模型参数的平方和作为惩罚项。

LL2=∑i=1n(yi−y^i)2+λ∑j=1kβj2{L_{\mathrm{L2}}=\sum_{i=1}^n(y_i-\hat{y}i)^2+\lambda\sum{j=1}^k\beta_j^2}LL2=∑i=1n(yi−y^i)2+λ∑j=1kβj2

---

第四章 分类分析

二分类、多分类、多标签分类的区别与联系

	特征	应用场景	常用算法
二分类	每个训练样本的标签 只有两种可能	例如，判断某以电影是否 为国产电影	逻辑回归 SVM 贝叶斯二分类器
多分类	每次只能选择其中的 一个标签	每个训练样本的标签例如，将某一电影分类为 可能有多种情况，但 动作、奇幻、喜剧、恐怖、 爱情、纪录片等多种类别 之一	随机森林 XGBoost 贝叶斯多分类器
分类	多标签每个训练样本同时可 以有多个标签	例如，对某电影添加"英 语"、"喜剧片"和"好 莱坞"等多个标签	神经网络算法

分类算法的关键------分类依据

分类算法	分类依据
KNN	相似度 (距离)
朴素贝叶斯分类	贝叶斯公式 (条件概率)
支持向量机	超平面
逻辑回归	对数几率
决策树	不纯度 (信息增量/信息增率)
随机森林	不纯度 (gini系数)

KNN算法

对于待预测样本 x，在训练集中找到与 x 距离最近的 K 个样本（称为 "K 近邻"），再根据这 K 个近邻的信息投票（分类任务）或取平均（回归任务），得到 x 的预测结果。

• 优点：
  • 算法思想简单易理解，实现起来比较容易，在解决分类和回归问题上应用较广；
  • 不需要设定复杂的规则，只要训练样本集本身来实现对未知样本的分类
• 缺点：
  • 占用存储空间大。KNN算法作为一种非参数的分类算法，需要将所有的训练样本都存储起来，如果样本集过大则增大了内存空间的负担：
  • 分类效率低。对于一个未知分类样本，实行KNN算法时都需要计算其与训练集每一个样本数据的相似度，进而确定出最佳k值，在处理大规模数据方面时间和空间复杂度高。

贝叶斯分类

朴素贝叶斯是一种基于贝叶斯定理 和特征条件独立假设的监督学习算法，核心优势是简单高效、对小规模数据友好，常用于分类任务（如文本分类、垃圾邮件识别、疾病诊断等）。

一、核心基础

1. 核心假设

特征条件独立性：假设样本的多个特征之间相互独立（"朴素"的由来），即某个特征的取值不影响其他特征的取值，这一假设大幅简化了计算复杂度。

2. 贝叶斯定理

对于分类任务，目标是根据样本特征 X=(x1,x2,...,xn)X=(x_1,x_2,...,x_n)X=(x1,x2,...,xn) 预测其所属类别 YYY，核心公式为：
P(Y=c∣X)=P(X∣Y=c)⋅P(Y=c)P(X)P(Y=c|X) = \frac{P(X|Y=c) \cdot P(Y=c)}{P(X)}P(Y=c∣X)=P(X)P(X∣Y=c)⋅P(Y=c)

• P(Y=c∣X)P(Y=c|X)P(Y=c∣X)：后验概率（待求），表示"已知特征 XXX 时，样本属于类别 ccc 的概率"；
• P(Y=c)P(Y=c)P(Y=c)：先验概率，表示"样本属于类别 ccc 的概率"（由训练集统计得到）；
• P(X∣Y=c)P(X|Y=c)P(X∣Y=c)：似然概率，表示"在类别 ccc 下，样本特征为 XXX 的概率"；
• P(X)P(X)P(X)：证据因子（与类别无关，可视为常数），比较不同类别时可忽略，仅需比较分子大小。

3. 特征条件独立下的简化

因假设特征独立，P(X∣Y=c)=∏i=1nP(xi∣Y=c)P(X|Y=c) = \prod_{i=1}^n P(x_i|Y=c)P(X∣Y=c)=∏i=1nP(xi∣Y=c)（多个独立事件的联合概率=各自概率的乘积），最终预测规则为：
Y^=arg⁡max⁡c[P(Y=c)⋅∏i=1nP(xi∣Y=c)]\hat{Y} = \arg\max_c \left[ P(Y=c) \cdot \prod_{i=1}^n P(x_i|Y=c) \right]Y^=argcmax[P(Y=c)⋅i=1∏nP(xi∣Y=c)]

即选择"先验概率×似然概率乘积"最大的类别作为预测结果。

二、计算例题（文本分类：判断邮件是否为垃圾邮件）

例题背景

已知训练集包含10封邮件，其中4封垃圾邮件（标记为C1C_1C1），6封正常邮件（标记为C2C_2C2）。提取邮件中的关键词特征（简化为3个："优惠""转账""会议"），统计结果如下：

类别	包含"优惠"的邮件数	包含"转账"的邮件数	包含"会议"的邮件数	总邮件数
垃圾邮件C1C_1C1	3	3	1	4
正常邮件C2C_2C2	1	0	5	6

待预测邮件 ：包含特征X=X=X=（"优惠"，"转账"，"会议"），判断该邮件是否为垃圾邮件？

步骤1：计算先验概率P(Y=c)P(Y=c)P(Y=c)

先验概率=某类别邮件数/总邮件数：

• P(C1)=垃圾邮件数总邮件数=410=0.4P(C_1) = \frac{\text{垃圾邮件数}}{\text{总邮件数}} = \frac{4}{10} = 0.4P(C1)=总邮件数垃圾邮件数=104=0.4
• P(C2)=正常邮件数总邮件数=610=0.6P(C_2) = \frac{\text{正常邮件数}}{\text{总邮件数}} = \frac{6}{10} = 0.6P(C2)=总邮件数正常邮件数=106=0.6

步骤2：计算似然概率P(xi∣Y=c)P(x_i|Y=c)P(xi∣Y=c)（拉普拉斯平滑）

似然概率=某类别中包含特征xix_ixi的邮件数/该类别总邮件数。

⚠️ 为避免"概率为0"（如正常邮件中无"转账"，直接计算P(转账∣C2)=0P(\text{转账}|C_2)=0P(转账∣C2)=0，导致乘积为0），需使用拉普拉斯平滑 ：
P(xi∣Y=c)=类别c中包含xi的样本数+1类别c的总样本数+特征取值数P(x_i|Y=c) = \frac{\text{类别}c\text{中包含}x_i\text{的样本数} + 1}{\text{类别}c\text{的总样本数} + \text{特征取值数}}P(xi∣Y=c)=类别c的总样本数+特征取值数类别c中包含xi的样本数+1

本题中每个特征的取值为"包含/不包含"（2种取值），但简化为"是否包含关键词"，故对每个特征，平滑公式简化为：
P(xi∣c)=包含xi的数量+1类别c总数量+2P(x_i|c) = \frac{\text{包含}x_i\text{的数量} + 1}{\text{类别}c\text{总数量} + 2}P(xi∣c)=类别c总数量+2包含xi的数量+1（+2是因为每个特征有2种可能）

计算各特征的似然概率：

1. 垃圾邮件C1C_1C1下：

   • P(优惠∣C1)=3+14+2=46≈0.667P(\text{优惠}|C_1) = \frac{3+1}{4+2} = \frac{4}{6} \approx 0.667P(优惠∣C1)=4+23+1=64≈0.667
   • P(转账∣C1)=3+14+2=46≈0.667P(\text{转账}|C_1) = \frac{3+1}{4+2} = \frac{4}{6} \approx 0.667P(转账∣C1)=4+23+1=64≈0.667
   • P(会议∣C1)=1+14+2=26≈0.333P(\text{会议}|C_1) = \frac{1+1}{4+2} = \frac{2}{6} \approx 0.333P(会议∣C1)=4+21+1=62≈0.333

2. 正常邮件C2C_2C2下：

   • P(优惠∣C2)=1+16+2=28=0.25P(\text{优惠}|C_2) = \frac{1+1}{6+2} = \frac{2}{8} = 0.25P(优惠∣C2)=6+21+1=82=0.25
   • P(转账∣C2)=0+16+2=18=0.125P(\text{转账}|C_2) = \frac{0+1}{6+2} = \frac{1}{8} = 0.125P(转账∣C2)=6+20+1=81=0.125
   • P(会议∣C2)=5+16+2=68=0.75P(\text{会议}|C_2) = \frac{5+1}{6+2} = \frac{6}{8} = 0.75P(会议∣C2)=6+25+1=86=0.75

步骤3：计算"先验×似然"的乘积（忽略P(X)P(X)P(X)）

1. 属于垃圾邮件C1C_1C1的概率分子：

P(C1)⋅P(优惠∣C1)⋅P(转账∣C1)⋅P(会议∣C1)=0.4×0.667×0.667×0.333≈0.4×0.148≈0.059 \begin{align*} P(C_1) \cdot P(\text{优惠}|C_1) \cdot P(\text{转账}|C_1) \cdot P(\text{会议}|C_1) &= 0.4 \times 0.667 \times 0.667 \times 0.333 \\ &\approx 0.4 \times 0.148 \approx 0.059 \end{align*} P(C1)⋅P(优惠∣C1)⋅P(转账∣C1)⋅P(会议∣C1)=0.4×0.667×0.667×0.333≈0.4×0.148≈0.059

2. 属于正常邮件C2C_2C2的概率分子：

P(C2)⋅P(优惠∣C2)⋅P(转账∣C2)⋅P(会议∣C2)=0.6×0.25×0.125×0.75≈0.6×0.0234≈0.014 \begin{align*} P(C_2) \cdot P(\text{优惠}|C_2) \cdot P(\text{转账}|C_2) \cdot P(\text{会议}|C_2) &= 0.6 \times 0.25 \times 0.125 \times 0.75 \\ &\approx 0.6 \times 0.0234 \approx 0.014 \end{align*} P(C2)⋅P(优惠∣C2)⋅P(转账∣C2)⋅P(会议∣C2)=0.6×0.25×0.125×0.75≈0.6×0.0234≈0.014

步骤4：决策判断

比较两个乘积大小：0.059>0.0140.059 > 0.0140.059>0.014，因此预测该邮件属于垃圾邮件C1C_1C1。

朴素贝叶斯分类的三种基本类型

	似然P(e|H)的分布	Scikit-learn包中的函数	原理
高斯贝叶斯	高斯分布 (正态分布)	GaussianNB	使用了高斯朴素贝叶斯算法进行分类，即假设模型中特征的似然符合正态分布，因此适用于连续变量居多的特征
多项式贝叶斯	多项式分布	MultinomialNB	假设了模型中特征的似然符合多项式分布，因此适用于多元离散的特征变量，经常被应用于文本分类中。
伯努利贝叶斯	伯努利分布 (0-1分布)	BernoulliNB	假设了模型中特征的似然符合二元伯努利分布，适用于二元离散的特征变量，即特征变量为布尔变量或者只有两种取值的变量。

SVM

一、SVM的定义

SVM（Support Vector Machine，支持向量机）是一种监督学习算法，核心目标是在特征空间中找到一个最优超平面，实现对不同类别样本的精准分隔，同时最大化超平面与两侧最近样本（支持向量）之间的距离（即间隔最大化）。

SVM的核心优势在于：

• 适用于高维数据（如文本分类、图像特征分类），且不易过拟合；
• 通过核函数可处理非线性分类问题（无需手动进行复杂的特征映射）；
• 仅依赖少数支持向量，计算效率较高。

其本质是一个凸二次规划问题，通过求解最优超平面的参数，实现对新样本的分类预测。

二、SVM的重要参数

SVM的参数直接影响模型的分隔效果和泛化能力，核心参数可分为模型结构参数 和训练优化参数两类，以下是关键参数详解：

1. 核函数（Kernel Function）

作用

解决非线性分类问题的核心：将低维线性不可分的数据映射到高维特征空间，使其在高维空间中线性可分，且无需显式计算高维映射（通过核技巧简化计算）。

常用类型

核函数类型	表达式	适用场景	特点
线性核（Linear）	K(xi,xj)=xi⋅xjK(x_i,x_j) = x_i \cdot x_jK(xi,xj)=xi⋅xj（向量内积）	数据本身线性可分，或特征维度高（如文本TF-IDF）	计算速度最快，可解释性强
多项式核（Polynomial）	K(xi,xj)=(γxi⋅xj+r)dK(x_i,x_j) = (\gamma x_i \cdot x_j + r)^dK(xi,xj)=(γxi⋅xj+r)d	数据存在低阶非线性关系（如简单曲线分隔）	需调节参数多（γ,r,d\gamma, r, dγ,r,d），计算复杂度中等
高斯核（RBF，径向基核）	K(xi,xj)=exp⁡(−γ∣xi−xj∣2)K(x_i,x_j) = \exp(-\gamma |x_i - x_j|^2)K(xi,xj)=exp(−γ∣xi−xj∣2)	大多数非线性场景（如复杂分类边界、图像分类）	适用范围最广，灵活性强，但需调优γ\gammaγ避免过拟合
Sigmoid核	K(xi,xj)=tanh⁡(γxi⋅xj+r)K(x_i,x_j) = \tanh(\gamma x_i \cdot x_j + r)K(xi,xj)=tanh(γxi⋅xj+r)	模拟神经网络，适用于二分类问题	稳定性较差，不如RBF常用

关键说明

• 优先尝试线性核（计算快、易解释），若效果不佳再换RBF；
• RBF是实际应用中最常用的核函数，因其适配多数复杂数据分布。

2. 惩罚系数（C）

作用

平衡"间隔最大化"和"分类错误最小化"的权重，控制模型的正则化强度。

参数影响

• CCC 越大：惩罚分类错误的力度越强，模型更倾向于让所有样本正确分类，可能导致间隔变小，容易过拟合（对噪声敏感）；
• CCC 越小：惩罚力度越弱，模型更注重间隔最大化，允许少量样本分类错误，容易欠拟合；
• 取值范围：通常为 0.001,0.01,0.1,1,10,1000.001, 0.01, 0.1, 1, 10, 1000.001,0.01,0.1,1,10,100 等（对数尺度取值），需通过交叉验证选择。

3. 核函数相关参数

不同核函数有专属参数，核心是调节核函数的"复杂度"：

（1）γ\gammaγ（Gamma）

• 仅适用于RBF核、多项式核、Sigmoid核，核心影响核函数的局部性。
• 影响规律：
  • γ\gammaγ 越大：核函数的局部性越强，模型仅关注样本附近的局部信息，容易过拟合（决策边界复杂，贴合训练数据）；
  • γ\gammaγ 越小：核函数的全局影响越强，模型关注整体数据分布，容易欠拟合（决策边界趋于简单）；
• 取值范围：通常为 0.001,0.01,0.1,1,10,1000.001, 0.01, 0.1, 1, 10, 1000.001,0.01,0.1,1,10,100 等，需与 CCC 联合调优。

（2）多项式核的额外参数

• ddd（degree）：多项式的阶数，控制非线性程度。ddd 越大，多项式越复杂，易过拟合（通常取1-5，d=1d=1d=1 等价于线性核）；
• rrr（coef0）：常数项，调节核函数的偏移量，影响低阶项的权重（默认值为0，需根据数据调整）。

4. 软间隔参数（ϵ\epsilonϵ，仅回归任务SVR适用）

SVM不仅可用于分类（SVC），也可用于回归（SVR，支持向量回归），ϵ\epsilonϵ 是SVR的核心参数：

• 作用：定义"ϵ\epsilonϵ-不敏感带"，即预测值与真实值的误差在 ϵ\epsilonϵ 范围内时，不计算损失，仅惩罚超出该范围的误差；
• 影响：ϵ\epsilonϵ 越大，不敏感带越宽，模型允许的误差越大，拟合越宽松（易欠拟合）；ϵ\epsilonϵ 越小，模型对误差越敏感（易过拟合）。

5. 其他辅助参数

• class_weight ：用于不平衡分类问题，指定不同类别的权重（如 class_weight='balanced' 自动根据样本数量调整权重，避免多数类主导模型）；
• max_iter：迭代次数上限，控制训练时间（默认值较大，数据量大时可减小以提升速度，但需确保模型收敛）；
• tol ：收敛阈值，当迭代过程中目标函数的变化小于tol时，停止训练（默认值为 1e−31e-31e−3，需平衡训练效率和模型精度）。

三、核心参数调优逻辑

SVM的参数调优核心是平衡过拟合与欠拟合，常用逻辑：

1. 先选择核函数：线性数据用线性核，非线性数据优先试RBF；
2. 调优 CCC 和 γ\gammaγ（RBF核）：CCC 控制正则化强度，γ\gammaγ 控制局部性，两者需联合通过网格搜索（GridSearchCV）或随机搜索（RandomizedSearchCV）优化；
3. 多项式核需额外调优 ddd 和 rrr，避免阶数过高导致过拟合。

逻辑回归

一、逻辑回归的定义

逻辑回归是一种监督学习算法 ，虽名为"回归"，实则主要用于分类任务（二分类为基础，可扩展至多分类）。其核心逻辑是：

1. 基于线性回归模型（z=w⋅x+bz = w \cdot x + bz=w⋅x+b，www 为权重，bbb 为偏置）输出连续值；
2. 通过Sigmoid函数 （也叫逻辑函数）将连续值映射到 [0,1][0,1][0,1] 区间，得到样本属于某一类别的概率；
3. 设定阈值（默认0.5），概率≥阈值则预测为正类，否则为负类。

Sigmoid函数表达式：σ(z)=11+e−z\sigma(z) = \frac{1}{1 + e^{-z}}σ(z)=1+e−z1

核心特点

• 模型简单、训练速度快，可解释性强（权重 www 能反映特征对分类结果的影响程度）；
• 适用于高维数据（如文本分类），但对非线性数据拟合能力弱（需结合特征工程或核技巧）；
• 本质是对数几率回归：建模的是"样本属于正类的对数几率"与特征的线性关系。

适用场景

二分类任务（如垃圾邮件识别、疾病诊断）、多分类任务（如数字识别）、概率预测（如用户购买概率）。

二、Sklearn中逻辑回归的重要参数（sklearn.linear_model.LogisticRegression）

Sklearn的LogisticRegression类封装了丰富参数，核心可分为模型结构参数 、正则化参数 、优化器参数三类，以下是关键参数详解：

1. 核心结构参数（决定模型类型和输出形式）

penalty：正则化方式（控制过拟合的核心）

• 作用：对模型权重 www 施加惩罚，避免权重过大导致过拟合（逻辑回归是线性模型，易因特征过多或权重极端出现过拟合）。
• 可选值：
  • 'l1'：L1正则化（Lasso），会使部分权重变为0，实现特征选择（适合冗余特征多的场景）；
  • 'l2'：L2正则化（Ridge），仅压制权重大小，不消除特征（默认值，适用多数场景，稳定性更强）；
  • 'elasticnet'：L1+L2混合正则化（需配合 l1_ratio 参数使用，兼顾特征选择和权重平滑）；
  • None：无正则化（不推荐，仅当数据特征少且无噪声时使用）。
• 注意：penalty='l1' 或 'elasticnet' 时，优化器需指定为 solver='saga'（其他优化器不支持L1正则）。

C：正则化强度的倒数（与SVM的C含义一致）

• 作用：平衡"模型拟合数据"和"正则化惩罚"的权重。
• 取值逻辑：
  • CCC 越大：正则化强度越弱，模型更倾向于拟合训练数据，易过拟合；
  • CCC 越小：正则化强度越强，权重被压制越明显，易欠拟合；
• 常用取值：0.001,0.01,0.1,1,10,1000.001, 0.01, 0.1, 1, 10, 1000.001,0.01,0.1,1,10,100（对数尺度取值，需通过交叉验证调优）。

multi_class：多分类策略（二分类时无需关注）

• 作用：指定逻辑回归处理多分类问题的方式。
• 可选值：
  • 'ovr'（One-vs-Rest，默认）：将每个类别视为"正类"，其他所有类别视为"负类"，训练多个二分类模型，最终取概率最大的类别；
  • 'multinomial'：直接建模多分类的对数几率（softmax回归），输出每个类别的概率分布，更适合类别间互斥的场景（如数字识别）；
  • 'auto'：自动根据数据类别数选择（二分类用ovr，多分类用multinomial）。
• 注意：multi_class='multinomial' 时，优化器需指定为 solver='lbfgs'/'saga'/'newton-cg'（不支持solver='liblinear'）。

class_weight：类别权重（处理不平衡数据）

• 作用：为不同类别分配不同权重，解决样本数量不均衡导致的模型偏向多数类问题。
• 可选值：
  • None（默认）：所有类别权重相同；
  • 'balanced'：自动根据样本数量计算权重（权重 = 总样本数 / (类别数 × 该类样本数)），多数类权重小，少数类权重大；
  • 字典形式：手动指定权重（如 class_weight={0:0.1, 1:0.9}，适合已知类别重要性的场景）。

2. 优化器与训练参数（控制模型训练过程）

solver：优化算法（求解模型权重的方法）

• 作用：选择最小化损失函数（对数损失）的优化器，直接影响训练速度和收敛效果。

• 可选值及适用场景：

  solver	适用场景	支持的正则化	特点
  liblinear	二分类问题（默认）、小数据集	L1、L2	速度快，不支持多分类multinomial
  lbfgs	二分类/多分类、中大数据集	L2、None	收敛快，数值稳定性好
  newton-cg	二分类/多分类、特征数较少的数据集	L2、None	依赖海森矩阵，精度高
  sag	大数据集（样本数>10万）、高维数据	L2、None	随机梯度下降，训练快
  saga	大数据集、高维数据、需要L1/ElasticNet正则	L1、L2、ElasticNet	最灵活，支持所有正则化方式

max_iter：最大迭代次数

• 作用：控制优化器的迭代上限，确保模型收敛（若迭代次数不足，模型可能未找到最优解）。
• 默认值：100（小数据集足够）；
• 调整建议：大数据集或正则化强度大时，需增大（如500、1000），避免因未收敛导致精度低；小数据集可减小以提升速度。

tol：收敛阈值

• 作用：当迭代过程中损失函数的下降量小于tol时，认为模型已收敛，停止训练。
• 默认值：1e−41e-41e−4（10的负4次方）；
• 调整建议：需要更高精度时，可减小（如1e−51e-51e−5），但会增加训练时间；追求速度时，可增大（如1e−31e-31e−3）。

3. 其他实用参数

fit_intercept：是否拟合偏置项 bbb

• 作用：控制模型是否包含常数项（偏置 bbb），偏置项可提升模型拟合能力（避免因特征中心化导致的偏差）。
• 可选值：True（默认，推荐）、False（仅当特征已中心化且无需偏置时使用）。

l1_ratio：ElasticNet的混合比例（仅penalty='elasticnet'时生效）

• 作用：控制L1和L2正则化的权重比例，表达式为：penalty=l1_ratio×L1+(1−l1_ratio)×L2penalty = l1\_ratio \times L1 + (1 - l1\_ratio) \times L2penalty=l1_ratio×L1+(1−l1_ratio)×L2。
• 取值范围：[0,1][0,1][0,1]，l1_ratio=1l1\_ratio=1l1_ratio=1 等价于L1正则，l1_ratio=0l1\_ratio=0l1_ratio=0 等价于L2正则。

verbose：训练日志输出

• 作用：控制训练过程中是否输出日志（如迭代次数、损失值）。
• 可选值：0（默认，不输出）、1（输出简要日志）、2（输出详细日志）；
• 适用场景：调试模型时（如查看是否收敛）可设为1，正式训练时设为0。

三、核心参数调优逻辑

逻辑回归的调优核心是平衡过拟合与训练效率，常用步骤：

1. 确定任务类型：二分类/多分类，是否存在类别不平衡；
2. 选择正则化方式（penalty）：
   • 特征冗余多→penalty='l1'（配合solver='saga'）；
   • 需兼顾平滑与选择→penalty='elasticnet'（配合l1_ratio）；
   • 普通场景→默认penalty='l2'；
3. 调优正则化强度（C）：通过网格搜索（GridSearchCV）测试0.01,0.1,1,100.01, 0.1, 1, 100.01,0.1,1,10等，找到最优值；
4. 选择优化器（solver）：
   • 小数据集/二分类→liblinear；
   • 中大数据集→lbfgs/sag；
   • 需L1正则→saga；
5. 调整训练参数：若模型未收敛（日志提示ConvergenceWarning），增大max_iter或减小tol。

LabelEncoder()的参数

• .fit(x)：输入数据并记录编码标签。
• .classes_：返回输入fit()方法中数据的不同取值。
• .transform(x):根据fit()方法中生成的编码，对输入的数据进行转换。
• .fit_transform(x):对输入的数据进行编码并转换。
• .inverse_transform(y):对输入的数据根据fit()方法下的编码逆向转换。

GridSearchCV()及其原理

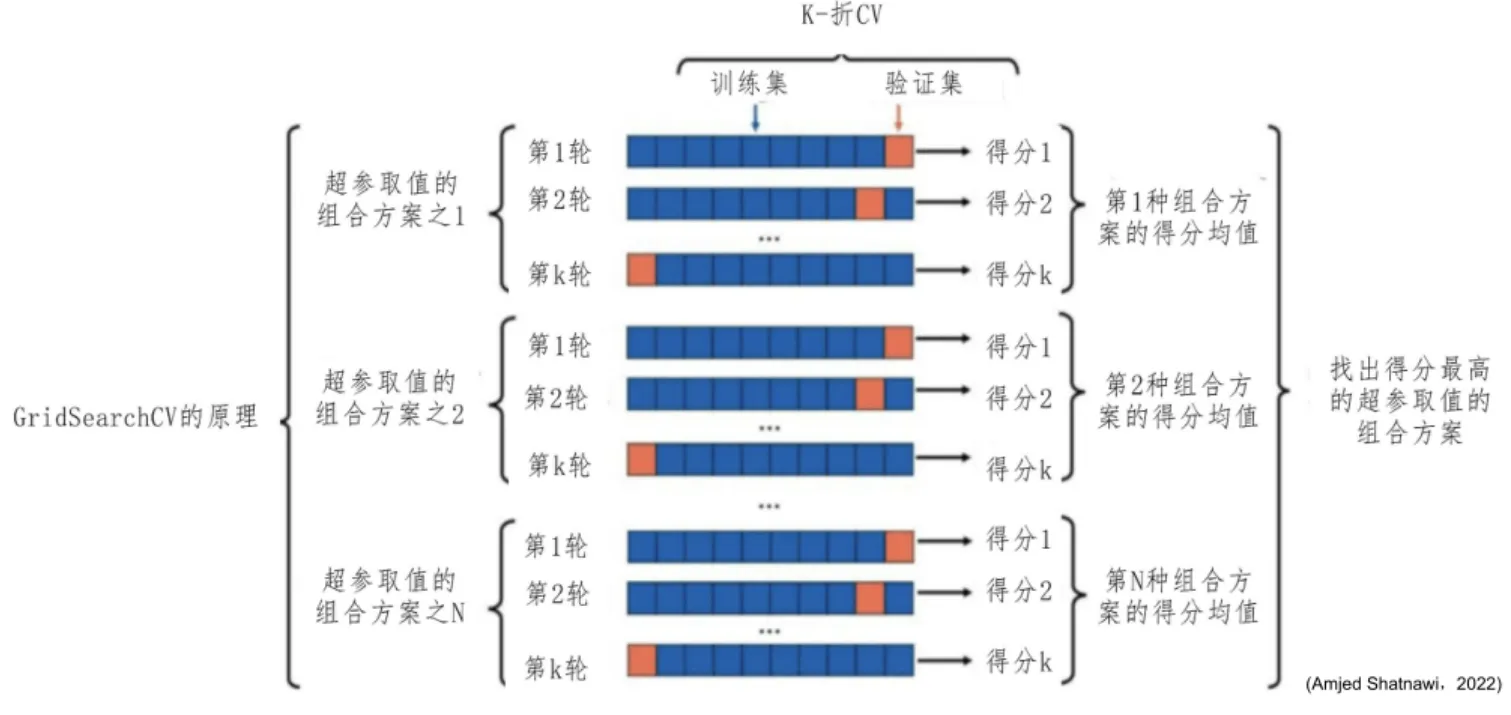
GridSearchCV（Grid Search with Cross-Validation，网格搜索交叉验证）是 sklearn 中用于自动化参数调优的核心工具，本质是"穷举搜索 + 交叉验证"的结合------通过遍历所有预设的参数组合，用交叉验证评估每个组合的模型性能，最终选择最优参数组合。

它完美解决了手动调参效率低、依赖经验的问题，是机器学习模型优化的必备工具。

一、核心原理

1. 核心逻辑：穷举 + 交叉验证

GridSearchCV 的工作流程可以拆解为 3 步，核心是"遍历所有可能，用交叉验证选最优"：

步骤 1：定义参数网格（Parameter Grid）

用户指定需要调优的参数及候选值，形成一个"参数组合网格"。

例如：SVM 的 C 候选值为 [0.1, 1, 10]，gamma 候选值为 [0.001, 0.01, 0.1]，则网格包含 3×3=9 个参数组合。

步骤 2：交叉验证评估每个组合

对每个参数组合，用 k 折交叉验证（k-fold CV） 评估模型性能：

• 将训练集分成 k 份（默认 k=5）；
• 每次用 k-1 份作为训练集，1 份作为验证集，训练并评估模型；
• 重复 k 次，得到 k 个验证分数，取平均值作为该参数组合的"交叉验证分数"（如准确率、F1 分数）。

步骤 3：选择最优参数组合

遍历完所有参数组合后，选择"交叉验证分数最优"（默认是最高，可通过 scoring 参数指定）的参数组合作为最终模型参数。

2. 为什么需要交叉验证？

如果直接用"训练集训练、验证集评估"选择参数，可能出现"参数适配验证集但泛化能力差"的问题（即验证集过拟合）。

而交叉验证通过多次拆分训练集/验证集，用平均分数评估参数，能更稳健地反映参数的泛化能力，避免单次拆分的随机性影响。

二、GridSearchCV 核心参数（sklearn.model_selection.GridSearchCV）

GridSearchCV 的参数分为两类：待调优的模型参数 和 网格搜索自身的配置参数，以下是关键参数详解：

1. 必选核心参数

参数名	作用	示例
estimator	指定要调优的模型（如 LogisticRegression、SVC），必须是 sklearn 兼容模型	estimator=LogisticRegression()
param_grid	字典格式的参数网格，key 是模型的参数名，value 是该参数的候选值列表	param_grid={'C': [0.1,1,10], 'penalty': ['l1','l2']}

2. 交叉验证相关参数

参数名	作用	可选值/默认值
cv	交叉验证的折数（k），或自定义交叉验证策略	整数（默认 5）、cv 生成器（如 StratifiedKFold）
scoring	评估模型性能的指标（决定"最优参数"的判断标准）	字符串（如 'accuracy'、'f1'）、自定义评分函数
refit	搜索完成后，是否用最优参数在完整训练集 上重新训练模型（推荐 True）	True（默认）、False

3. 效率与输出控制参数

参数名	作用	可选值/默认值
n_jobs	并行运行的任务数（加速搜索），-1 表示使用所有 CPU 核心	整数（默认 1）、-1（推荐）
verbose	输出日志的详细程度（0=无日志，1=简要，2=详细）	0（默认）、1、2
error_score	当某参数组合训练失败时，是否报错或赋值为指定分数（如 np.nan）	'raise'（默认，报错）、np.nan

关键参数补充说明

（1）scoring 常用取值（根据任务选择）

• 二分类：'accuracy'（准确率）、'f1'（F1 分数，适合不平衡数据）、'roc_auc'（AUC 分数）；
• 多分类：'accuracy'、'f1_macro'（宏平均 F1）、'f1_weighted'（加权 F1）；
• 回归：'r2'（R² 分数）、'neg_mean_squared_error'（负均方误差，注意是"负"值，分数越高越好）。

（2）cv 的特殊用法

对于不平衡分类数据 ，建议用 StratifiedKFold（分层 k 折），确保每折的类别分布与原数据一致：

from sklearn.model_selection import StratifiedKFold
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)  # 分层+打乱

---

第五章 聚类分析

	分类分析	聚类分析
命名方法	类别（Class）	类簇（Cluster)
算法类型	有监督学习	无监督学习
计算过程	分两个阶段进行	一个阶段直接完成
典型算法	决策树 贝叶斯分类 SVM	k-means DBScan 层次聚类

---

第六章 集成学习

专业术语

术语类型	定义	补充说明
基学习器	集成学习的个体学习器是同质的（homogeneous），即个体学习器属于同种类型	又称baselearner
组件学习器	集成学习的个体学习器是异质的（heterogeneous），即由不同类型的算法组成	又称componentlearner
弱学习器	泛化性能略优于随机猜测（random guessing）的学习器，如二分类问题上精度略高于50%的分类器	-
NFL没有免费的午餐定理	常用于机器学习和搜索/优化领域，指没有一个机器学习算法在所有可能的函数中能比随机猜测更好，每个算法必须包含数据之外的知识或假设才能将数据一般化	是机器学习和优化领域的重要定理

同质集成学习和异质集成学习

	同质集成学习	异质集成学习
特征	个体学习器为同质或同一类型算法	个体学习器为异质或不同类型的算法
举例	随机森林	使用投票机制结合决策树、SVM 和逻辑回 归来改进预测结果的用户自定义算法
个体学习 器的名称	基学习器（Base Learner)	组件学习器（ComponentLearner）

集成学习类型

集成学习类型	核心思想	训练方式	代表算法	特点
Bagging法	并行训练多个基模型，通过投票或平均降低方差	各基模型独立训练，样本和特征有放回随机抽样（如随机森林的样本Bootstrap、特征随机选择）	随机森林	抗噪性强，不易过拟合，可并行计算，适合高方差模型（如决策树）
Boosting法	串行训练基模型，后一个模型专注于修正前一个模型的错误，逐步提升性能	基模型依次训练，每个模型的权重根据前序模型的误差调整，样本权重随训练动态变化	AdaBoost、XGBoost、Gradient Boosting	精度高，可处理非线性关系，易过拟合（需正则化），训练串行、速度较慢
Stacking法	训练多层模型，第一层用多种基模型预测，第二层用新模型学习第一层的预测结果以输出最终结论	先训练多个基模型，再将基模型的预测结果作为新特征，训练元模型（如逻辑回归、SVM）	基于mlxtend的StackingClassifier	灵活性高，可融合多种模型的优势，但训练过程复杂，易过拟合（需合理设计基模型和元模型）

集成策略

集成策略	定义	具体方法	适用场景	示例（随机森林）
平均法（Averaging）	对多个个体学习器的预测结果取平均值，作为最终输出	简单平均（所有学习器预测值直接平均）、加权平均（给不同学习器分配不同权重后平均）	回归任务（如房价预测、销量预测）	随机森林回归任务中，采用多棵决策树预测结果的平均值作为最终预测值
投票法（Voting）	对多个个体学习器的分类预测结果进行投票，得票最多的类别作为最终分类	硬投票（直接统计类别得票数，得票最多的类别胜出）、软投票（统计每个类别在所有学习器中的预测概率平均值，概率最高的类别胜出）	分类任务（如垃圾邮件识别、图像分类）	随机森林分类任务中，多棵决策树对样本类别进行投票，得票最多的类别作为最终分类结果
堆叠法（Stacking）	先训练多个基学习器，将基学习器的预测结果作为新特征，再训练一个元学习器来学习这些新特征，从而得到最终预测结果	第一层：训练多个不同的基学习器（可同质或异质），得到基学习器的预测结果；第二层：将这些预测结果作为输入，训练元学习器（如逻辑回归、SVM等），输出最终结果	需进一步提升精度的复杂任务，可融合多种模型的优势	可结合决策树、SVM、逻辑回归等作为基学习器，以神经网络作为元学习器，对图像分类任务进行高精度预测

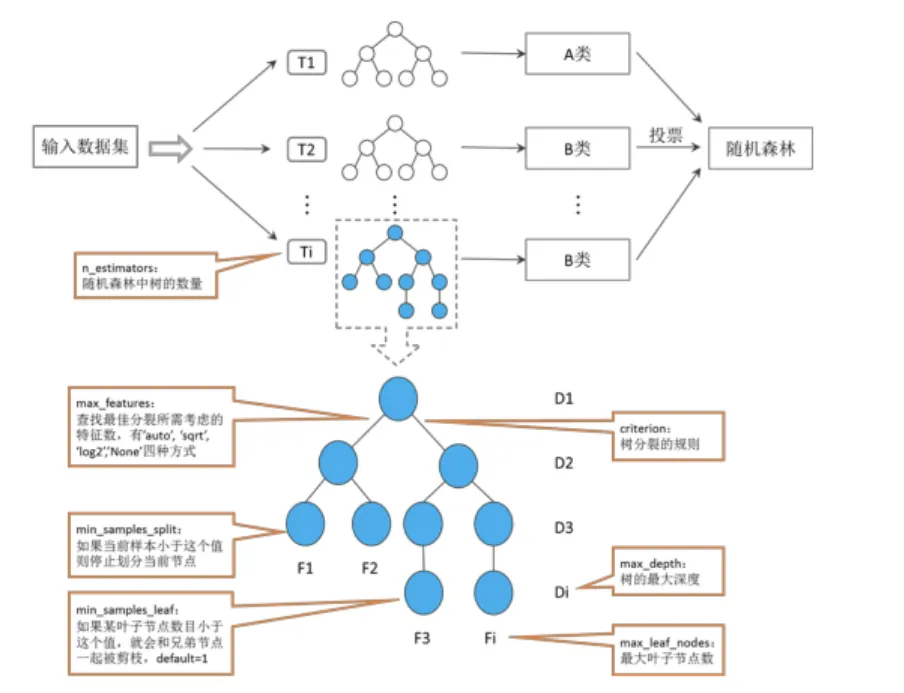
随机森林

随机森林是一种集成学习算法 ，属于 Bagging 方法的典型应用。它通过 随机抽样（样本和特征） 构建多棵决策树，最终以所有决策树的 "投票（分类任务）" 或 "平均（回归任务）" 结果作为模型输出。

核心优势

• 高鲁棒性：多棵树的集成有效降低了单棵决策树的过拟合风险；
• 强适应性：可处理分类、回归任务，对数值型、类别型特征均友好；
• 可解释性：能通过特征重要性分析判断特征对结果的影响程度；
• 并行性：各决策树独立训练，可高效利用计算资源。

关键参数

参数名称	参数含义	备注
n_estimators	随机森林中树的数量	default=10，默认10个基决策树
criterion	树分裂的规则	可选"gini"和"entropy"两种方式，default="gini"
max_depth	树的最大深度	default=None，默认树一直扩展，直到所有的叶子节点都是同一类样本，或者 达到最小样本划分（min_samples_split）的数目。
min_samples_split	最小样本划分的数目	如果当前样本小于这个值则停止划分当前节点，default=2
min_samples_leaf	叶子节点最小样本数	如果某叶子节点数目小于这个值，就会和兄弟节点一起被剪枝，default=1
min_weight fraction_leaf	叶子节点最小的权重和	default=0.0，默认为0，样本的权重相等 n_features为全部的特征数，---"auto"---"sqrt""log2"""-None""四种
max_features	查找最佳分裂所需考虑的特征数	模式分别表示max_features=sqrt(n_features)、 max_features=sqrt(n_features) max_features=log2(n_features) max_features=n_features.
max_leaf_nodes	最大叶子节点数	default=None，即不限制最大的叶子节点数
min_impurity_split	节点划分的最小不纯度	结束树增长的一个阅值，如果不纯度大于这个阈值，那么该节点就会继续划分！ 否则不划分，成为一个叶子节点
bootstrap	是否使用bootstrap方法采样	default=True，默认选择自助采样法
oob_score	是否使用袋外样本作为验证集估计模型 准确度	default=False，默认不采用
njobs	并行job个数	default=1，1：不并行；-1:跟CPU核数一致；n:n个并行，
random_state	随机数种子	default=None，默认由np.numpy生成

XGboost

XGBoost（Extreme Gradient Boosting）是一种高效的集成学习算法，属于Boosting家族，通过串行训练多棵决策树（基学习器），每棵树专注于修正前序树的误差，最终实现高精度预测。它在分类、回归、排序任务中表现优异，是数据竞赛和工业界的常用工具。

一、XGBoost 核心原理

XGBoost 基于梯度提升框架，核心特点：

• 正则化优化：在损失函数中加入正则项（L1/L2），有效防止过拟合；
• 并行加速：特征分裂时的候选节点计算可并行化，训练效率高；
• 灵活性强：支持自定义损失函数和评估指标，适配各类任务；
• 缺失值处理：内置缺失值处理逻辑，无需手动填充。

二、XGBoost 关键参数（以 Python xgboost 库为例）

以下表格整理了分类/回归任务中最核心的参数，按功能分类：

参数类别	参数名	含义与作用	常用取值范围/选项
模型结构	n_estimators	基学习器（决策树）的数量，树越多精度越高，但训练时间越长	100~1000（默认100）
	max_depth	单棵决策树的最大深度，控制树的复杂度，防止过拟合	3~10（默认6）
	learning_rate	学习率（步长），控制每棵树对整体模型的贡献，与 n_estimators 协同调优	0.01~0.3（默认0.1）
正则化	alpha（L1）	L1 正则化系数，压制权重绝对值，实现特征选择，防止过拟合	0~10（默认0）
	lambda（L2）	L2 正则化系数，压制权重平方和，使权重更平滑，防止过拟合	0~100（默认1）
	subsample	每棵树训练时的样本抽样比例（行抽样），增加样本多样性，防止过拟合	0.5~1（默认1）
	colsample_bytree	每棵树训练时的特征抽样比例（列抽样），增加特征多样性，防止过拟合	0.5~1（默认1）
损失与优化	objective	目标函数（损失函数），指定任务类型	分类：'binary:logistic'（二分类）、'multi:softmax'（多分类）；回归：'reg:squarederror'（默认）
	eval_metric	评估指标，用于验证集监控模型性能	分类：'auc'、'error'；回归：'rmse'、'mae'
其他关键	gamma	节点分裂的最小损失减少量，gamma 越大，树越难分裂，模型越简单	0~10（默认0）
	min_child_weight	叶节点的最小样本权重和，防止叶节点过拟合	1~10（默认1）
样），增加特征多样性，防止过拟合	0.5~1（默认1）
损失与优化	objective	目标函数（损失函数），指定任务类型	分类：'binary:logistic'（二分类）、'multi:softmax'（多分类）；回归：'reg:squarederror'（默认）
	eval_metric	评估指标，用于验证集监控模型性能	分类：'auc'、'error'；回归：'rmse'、'mae'
其他关键	gamma	节点分裂的最小损失减少量，gamma 越大，树越难分裂，模型越简单	0~10（默认0）
	min_child_weight	叶节点的最小样本权重和，防止叶节点过拟合	1~10（默认1）
	n_jobs	并行计算的线程数，加快训练速度	-1（使用所有线程）、1（默认）