数据结构===Map/Set （2）===

一，哈希表的核心基础概念（含底层逻辑，实例细节，边界情况）

1. 定义与核心思想（深入拆解）

严格定义 ：哈希表（散列表）是一种存储结构 ，通过哈希函数（散列函数） 将元素的关键码（Key） 映射为存储位置（数组下标） ，使 Key 与存储位置形成一一映射关系，实现 "无比较直接访问"。（说人话就是哈希表就是 "给东西定好规矩找'家'，以后不用瞎翻，直接按规矩取" 的好办法）。
核心目标 ：规避传统查找算法的多次比较开销 ------ 顺序查找需逐个比较（O (n)）、平衡树 / 红黑树需逐层比较（O (log₂n)），哈希表通过 "一次映射定位" 追求理想 O(1) 时间复杂度。

设计本质：用 "空间冗余" 换取 "时间效率"------ 通过预留额外空间（数组扩容、链表节点）降低冲突率，确保映射关系的有效性。
直观完整实例 ：
- 假设底层数组容量（capacity）=10，哈希函数 =「k mod 10」（后续会优化为质数除数）。
- 插入数据 1：1 mod 10=1 → 存入数组 1 下标。
- 插入数据 7：7 mod 10=7 → 存入数组 7 下标。
- 插入数据 6：6 mod 10=6 → 存入数组 6 下标。
- 插入数据 5：5 mod 10=5 → 存入数组 5 下标。
- 插入数据 18：18 mod 10=8 → 存入数组 8 下标。
- 查找数据 18：直接计算 18 mod 10=8 → 访问 8 下标即可取出，无需遍历其他位置。

2. 核心操作逻辑（含步骤拆解）

（1）插入操作（3 步）

接收待插入元素的 Key 和 Value；
通过哈希函数计算 Key 对应的哈希地址（数组下标）；
若地址为空，直接存入该位置；若地址已被占用（冲突），触发冲突解决机制（后续详解）。

（2）查找操作（3 步）

接收目标元素的 Key；
通过与插入时相同的哈希函数计算哈希地址；
访问该地址：若元素存在且 Key 匹配，返回 Value；若地址为空或 Key 不匹配，查找失败（或继续冲突探测）。

（3）删除操作（依赖冲突解决方式）

闭散列（线性 / 二次探测）：需用伪删除法（标记删除），不能直接清空位置；
开散列（哈希桶）：直接删除链表 / 红黑树中的对应节点，维护链表 / 树结构。

|---------|----------|---------------|----------------|
| 查找算法 | 时间复杂度 | 核心劣势 | 哈希表的改进点 |
| 顺序查找 | O(n) | 需逐个比较，效率极低 | 无比较，直接定位地址 |
| 平衡二叉树查找 | O(log₂n) | 需逐层比较，维护树平衡复杂 | 无比较，无需维护树结构 |
| 红黑树查找 | O(log₂n) | 需旋转维护平衡，操作繁琐 | 操作简单，冲突可控时效率更高 |
[核心优势对比表]

二、哈希冲突相关知识点（含本质原因与实例）

1. 哈希冲突的定义与相关概念（精准细化）

冲突严格定义 ：对于两个不同的关键码（KI ≠ KJ，i≠j），若通过同一哈希函数计算得到相同的哈希地址（Hash (KI)=Hash (KJ)） ，则称为哈希冲突（哈希碰撞）。
同义词定义 ：所有满足 "Key 不同但 Hash 地址相同" 的数据元素，互为同义词（如 Key=4、14、24、34，通过「k mod 10」计算均得地址 4，四者互为同义词）。
冲突的本质原因 ：
- 数学角度：哈希函数是 "多对一映射"------Key 的取值范围（如整数、字符串）远大于哈希地址的取值范围（0~m-1，m 为数组长度），必然存在不同 Key 映射到同一地址的情况；
- 工程角度：数组容量有限（受内存限制），无法为每个 Key 分配唯一地址，只能通过 "降低冲突率" 优化。

2. 冲突的必然性验证（实例量化）

假设数组长度 m=10，需存储 20 个 Key（1~20），哈希函数 =「k mod 10」；
所有 Key 的哈希地址仅能是 0~9（共 10 个地址），20 个 Key 需 "挤入" 10 个地址，每个地址至少分配 2 个 Key，冲突率 100%；
即使存储 11 个 Key，至少有 1 个地址分配 2 个 Key，冲突率≥10%，证明冲突无法避免。

三、避免哈希冲突的方法（冲突发生前，含底层原理）

1. 设计合理的哈希函数（含规则细节与实例推演）

（1）哈希函数的 3 条设计规则（逐条拆解）

规则 1：定义域全覆盖哈希函数的输入必须能接收所有待存储的 Key（无遗漏）。反例：若 Key 包含负数（如 - 1、-5），而哈希函数仅支持非负 Key 计算，则 - 1、-5 无法映射，违反该规则。
规则 2：值域合法哈希函数的输出（哈希地址）必须落在「0 ~ m-1」区间（m 为数组长度），不能超出数组下标范围。实例：数组长度 m=10，哈希地址必须是 0~9，若计算得到 10，则需通过 mod 10 调整为 0。
**规则 3：地址均匀分布（核心规则）**哈希函数需让 Key 的哈希地址均匀分散在 0~m-1 中，避免集中在某几个地址（否则冲突率飙升）。
量化标准 ：理想情况下，n 个 Key 的哈希地址在 m 个位置中均匀分布，每个位置的 Key 数量≈n/m（即负载因子 α）。

（2）常见哈希函数类型（含公式、实例、优缺点全解析）

① 直接定制法

公式：Hash (k) = a×k + b（a、b 为常数，k 为 Key，需是数值型）；
本质：Key 的线性变换，保持 Key 的分布特性；
实例 1：Key 为学生学号（10001、10002、10003），设 a=1，b=-10000，则 Hash (k)=k-10000 → 地址为 1、2、3，均匀分布；
实例 2：字符串 "第一个只出现一次的字符" 问题（Key 为字符）：字符的 ASCII 码是数值（如 'a'=97、'b'=98），设 a=1，b=-97，则 Hash (ch)=ch-'a' → 地址为 0~25（对应 26 个小写字母），无冲突；
优点：计算简单（仅加减乘）、地址绝对均匀（若 Key 本身均匀）；
缺点：仅适用于 Key 是数值型且分布已知的场景，若 Key 分布无序（如随机整数），则地址可能集中；
适用场景：Key 分布规律、数值连续的场景（如学号、序号）。

② 除留余数法（最常用）

公式：Hash (k) = k mod p（p 为除数，核心是 p 的选择）；
除数 p 的选择规则（3 条） ：
1. p 必须是质数（核心！质数的因数少，能减少地址重复）；
2. p≤m（数组长度），且尽量接近 m；
3. 避免 p 是 2 的幂（如 8、16）或 10 的倍数（如 10、20），这类数的因数多，易导致地址集中；
正确实例：数组长度 m=10，选择 p=7（质数，≤10 且接近 10）：Key=4 → 4 mod7=4；Key=14→14 mod7=0；Key=24→24 mod7=3；Key=34→34 mod7=6 → 地址分散，无冲突；
错误实例：选择 p=10（非质数）：Key=4→4、Key=14→4、Key=24→4、Key=34→4 → 地址集中，冲突率 100%；
优点：适用范围广（Key 可为任意整数）、计算简单（mod 运算高效）；
缺点：p 的选择直接影响冲突率，需提前确定质数 p；
适用场景：绝大多数场景（如 HashMap 的哈希地址计算，底层隐含 mod 质数操作）。

③ 平方取中法（适用于短 Key）

公式：Hash (k) = （k² 的中间几位）mod m；
原理：Key 的平方后，中间几位会融合 Key 的高低位特征，减少地址重复；
实例：Key=123，k²=15129（5 位），取中间 3 位 "512"，m=1000 → Hash (k)=512；Key=132，k²=17424，取中间 3 位 "742" → 地址不同，无冲突；
优点：适用于 Key 位数少、分布不规则的场景；
缺点：计算稍复杂（需平方运算），Key 位数过长时效果下降；
适用场景：Key 为短整数（如身份证后 4 位、手机号后 6 位）。

④ 数学分析法（适用于 Key 有固定格式）

原理：分析 Key 的数字特征，选择分布均匀的部分作为哈希地址，忽略重复率高的部分；
实例：Key 为身份证号（18 位）：前 6 位（地区）重复率高，中间 8 位（生日）分布均匀，后 4 位（序号）重复率低 → 取中间 8 位（生日）转为整数，再 mod p 得到哈希地址；
优点：针对性强，冲突率极低；
缺点：依赖 Key 的格式特征，通用性差；
适用场景：Key 有固定结构（如身份证号、手机号、地址编码）。

（3）实际开发使用原则（无例外）

开发中无需手动设计哈希函数：Java、C++ 等语言的集合框架（如 HashMap、unordered_map）已内置优化后的哈希函数，兼顾均匀性和效率；
若需自定义 Key（如自定义对象）：只需重写hashCode()方法（确保相同对象返回相同哈希值，不同对象尽量返回不同哈希值）和equals()方法（确保哈希地址相同时，Key 能正确比较）。

2. 调节负载因子（含数学推导、Java 源码细节）

（1）负载因子的定义与数学表达

严格公式：负载因子 α = 填入表中的元素个数 n / 散列表长度 m（α = n/m）；
物理意义：散列表的 "填充率"------α 越接近 1，表越满，冲突率越高；α 越接近 0，表越空，空间利用率越低；
实例计算 ：
- 数组长度 m=16，填入 n=12 → α=12/16=0.75（Java 默认阈值）；
- 扩容后 m=32，n=12 → α=12/32=0.375（冲突率大幅下降）。

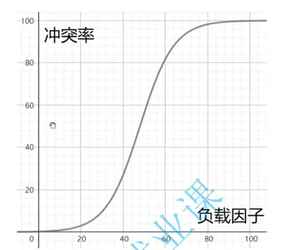
（2）负载因子与冲突率的定量关系

实验结论（Java 官方数据）：
- α=0.1：冲突率≈0.01（几乎无冲突）；
- α=0.5：冲突率≈0.1（少量冲突）；
- α=0.75：冲突率≈0.3（可接受冲突）；
- α=0.8：冲突率≈0.9（几乎每次插入都冲突）；
- α=1.0：冲突率≈1.0（所有插入都冲突）；
核心规律：冲突率随 α 的增大呈指数级上升，而非线性上升 ------α 超过 0.75 后，冲突率会急剧飙升。

（3）调节负载因子的底层逻辑（数学推导）

目标：降低冲突率 → 需降低 α；
推导：α = n/m → 要降低 α，有两种途径：
1. 减少 n（停止插入元素）：不现实（集合需存储数据）；
2. 增加 m（扩容散列表长度）：唯一可行途径；
结论：扩容是降低负载因子、减少冲突的唯一有效手段。

（4）Java 中的负载因子与扩容机制（源码级细节）

① 核心参数

默认初始数组长度：16（m=16）；
负载因子阈值：0.75（α_threshold=0.75）；
扩容触发条件：当 n ≥ α_threshold × m 时，触发扩容；
扩容规则：新数组长度 = 原数组长度 ×2（m_new=2×m_old），且新长度始终是 2 的幂（如 16→32→64→128）。

② 扩容实例推演

初始状态：m=16，α_threshold=0.75 → 触发扩容的 n=16×0.75=12；
插入第 12 个元素：n=12，α=12/16=0.75 → 触发扩容；
扩容后：m_new=32，α=12/32=0.375 → 冲突率大幅下降；
插入第 24 个元素：n=24，α=24/32=0.75 → 再次触发扩容，m_new=64。

③ 扩容的关键步骤（rehash 过程）

创建新数组（长度为原数组的 2 倍）；
遍历原数组中的每个桶（链表 / 红黑树）；
对每个桶中的元素，重新通过哈希函数计算新的哈希地址（因 m 变化，Hash (k)=k mod m 也变化）；
将元素插入新数组对应的桶中；
释放原数组内存，将新数组作为当前散列表的底层数组。

④ 扩容的注意事项

扩容是 "时间换空间" 的反向操作：扩容过程需遍历所有元素并重新计算地址，耗时与元素个数成正比（O (n)），但后续操作效率会显著提升；
避免频繁扩容：若已知需存储大量元素（如 1000 个），可提前指定初始容量（如new HashMap<>(2048)），减少扩容次数。

四、解决哈希冲突的方法（冲突发生后，含代码级细节）

1. 闭散列（开放地址法）------ 冲突元素存入原数组

核心思想 ：当 Key 的哈希地址已被占用时，若数组未装满，通过 "探测算法" 寻找数组中下一个空位置存储该元素，无需额外开辟空间。
适用场景：数组空间充足、元素个数较少的场景（如嵌入式设备、内存受限场景）。
两大探测方式（全细节拆解）：

（1）线性探测（Linear Probing）

① 探测规则

初始哈希地址：H0 = Hash (k)；
若 H0 被占用，探测 H1 = (H0 + 1) mod m；
若 H1 被占用，探测 H2 = (H0 + 2) mod m；
以此类推，直到找到空位置 Hi = (H0 + i) mod m（i=0,1,2,...m-1）；
若遍历 m 次仍未找到空位置，说明数组已满（溢出）。

② 完整实例推演

数组长度 m=10，哈希函数 =「k mod 10」，已存入 Key=4（H0=4）；
插入 Key=14：H0=14 mod10=4（被占用）→ 探测 H1=5（空）→ 存入 5 下标；
插入 Key=24：H0=24 mod10=4（被占用）→ H1=5（被占用）→ H2=6（空）→ 存入 6 下标；
插入 Key=34：H0=4→H1=5→H2=6（均被占用）→ H3=7（空）→ 存入 7 下标。

③ 核心问题：元素聚集（Clustering）

定义：冲突元素会 "扎堆" 形成连续的占用区域（如 4、5、6、7 下标），后续插入哈希地址在该区域附近的 Key（如 Key=5，H0=5）需多次探测才能找到空位置，导致探测次数增多，效率下降；
极端情况：若聚集区域覆盖数组大部分位置，插入 / 查找的时间复杂度接近 O (n)，失去哈希表的优势。

④ 删除问题与伪删除法（代码级实现）

删除问题：若直接删除聚集区域中的中间元素（如删除 Key=4），后续查找 Key=14 时，会因 H0=4 为空而误判 "Key=14 不存在"（探测停止于空位置）；
伪删除法解决方案 ：
- 数组元素结构：每个位置存储「Key、Value、isDeleted（布尔值）」；
- 删除逻辑：不清除 Key 和 Value，仅将 isDeleted 设为 true（标记为 "已删除"）；
- 查找逻辑：探测时遇到 isDeleted=true 的位置，继续向后探测（视为 "非空"）；
- 插入逻辑：isDeleted=true 的位置可被复用（视为 "空"）；

代码片段示例 ：

java

运行

java 复制代码

class HashTableClosed {
    static class Entry {
        int key;
        int value;
        boolean isDeleted; // 伪删除标记
        Entry(int key, int value) {
            this.key = key;
            this.value = value;
            this.isDeleted = false;
        }
    }
    private Entry[] table;
    private int capacity;
    // 查找逻辑
    public Integer get(int key) {
        int h0 = key % capacity;
        for (int i = 0; i < capacity; i++) {
            int hi = (h0 + i) % capacity;
            Entry entry = table[hi];
            if (entry == null) return null; // 真正的空位置，查找失败
            if (entry.key == key && !entry.isDeleted) return entry.value; // 找到目标元素
            // 若entry.isDeleted=true，继续探测
        }
        return null;
    }
}

伪删除法弊端：标记后的位置无法真正释放，若删除元素过多，isDeleted=true 的位置会增多，导致探测次数增加，空间利用率下降。

（2）二次探测（Quadratic Probing）------ 解决聚集问题

① 探测规则（公式推导）

核心改进：探测步长为 "i²"，而非线性探测的 "i"，分散冲突元素；
探测公式：Hi = (H0 ± i²) mod m（i=1,2,3,...；H0=Hash (k)；"±" 表示可向左或向右探测）；
选择逻辑：优先探测 "+i²"，若该位置被占用，再探测 "-i²"，确保分散性。

② 完整实例推演

数组长度 m=10（质数），已存入 Key=4（H0=4）；
插入 Key=14：H0=4（被占用）→ i=1，H1=(4+1²) mod10=5（空）→ 存入 5 下标；
插入 Key=24：H0=4（被占用）→ i=1，H1=5（被占用）→ i=2，H2=(4+2²) mod10=8（空）→ 存入 8 下标；
插入 Key=34：H0=4（被占用）→ i=1→5（占）→ i=2→8（占）→ i=3，H3=(4+3²) mod10=13mod10=3（空）→ 存入 3 下标；
结果：冲突元素分散在 3、5、8 下标，无聚集现象。

③ 约束条件（插入成功的必要条件）

（1）结构细节（JDK8+ HashMap）

① 底层结构组成

② 哈希值扰动函数（减少冲突的关键）

（2）核心操作逻辑（以插入为例）

① 插入步骤（JDK8+ 尾插法）

② 实例推演（数组长度 n=16，α=0.75）

（4）开散列的优缺点

优点	缺点
无元素聚集问题，冲突率低	需额外存储链表 / 红黑树节点，空间开销大
删除简单（直接删节点）	实现复杂（需维护链表 / 红黑树转换）
空间利用率高（α 可接近 1）	扩容时需 rehash 所有节点
操作效率稳定（接近 O (1)）	多线程环境下需处理并发安全问题（HashMap 非线程安全）

想省地方、东西少、不常扔→用闭散列（找邻居抽屉）；
东西多、常找常扔、不差地方→用开散列（自己抽屉加架子）。

五、哈希表与 Java 中的应用（代码案例）

一、统计单词个数

1. 带注释代码

java

运行

java 复制代码

import java.util.HashMap;
import java.util.Map;

public class CountWordFrequency {
    public static void main(String[] args) {
        String[] words = {"apple", "banana", "apple", "orange", "banana", "apple"};
        Map<String, Integer> frequencyMap = countWords(words);
        
        // 输出结果
        for (Map.Entry<String, Integer> entry : frequencyMap.entrySet()) {
            System.out.println(entry.getKey() + ": " + entry.getValue() + "次");
        }
    }

    /**
     * 统计字符串数组中每个单词的出现次数
     * @param words 输入的单词数组
     * @return 键为单词、值为出现次数的哈希表
     */
    public static Map<String, Integer> countWords(String[] words) {
        // 哈希表：利用键的唯一性存储单词，值存储次数（查询/插入O(1)）
        Map<String, Integer> map = new HashMap<>();
        
        // 遍历所有单词
        for (String word : words) {
            // 若单词未在哈希表中，初始化为1；已存在则次数+1
            map.put(word, map.getOrDefault(word, 0) + 1);
        }
        return map;
    }
}

2. 核心逻辑

利用 哈希表（HashMap） 的键唯一性，将「单词」作为键，「出现次数」作为值；
遍历单词数组，通过 getOrDefault 简化逻辑：不存在则默认次数为 0，存在则直接累加 1；
最后遍历哈希表输出键值对，得到每个单词的频率。

3. 核心重点

数据结构选择：哈希表是最优解，put 和 get 操作时间复杂度 O (1)，整体时间复杂度 O (n)（n 为单词个数）；
边界处理：空数组直接返回空哈希表，无需额外判断（getOrDefault 天然兼容）；
简化写法：map.getOrDefault(word, 0) + 1 替代 if-else 判断，代码更简洁。

二、只出现一次的数字

方法 1：异或运算（最优解）

1. 带注释代码

java

运行

java 复制代码

public class SingleNumberXOR {
    public static void main(String[] args) {
        int[] nums = {4, 1, 2, 1, 2};
        System.out.println("只出现一次的数字：" + singleNumber(nums));
    }

    /**
     * 异或运算求解：空间复杂度O(1)（最优）
     * @param nums 输入数组（只有一个元素出现1次，其余出现2次）
     * @return 只出现一次的数字
     */
    public static int singleNumber(int[] nums) {
        int result = 0; // 异或初始值：0异或任何数=原数
        for (int num : nums) {
            // 异或性质：a^a=0，a^0=a，且满足交换律/结合律
            // 所有出现2次的数字异或后为0，最终结果=0^唯一出现1次的数字
            result ^= num;
        }
        return result;
    }
}

2. 核心逻辑

利用异或运算的三大性质：
1. 任何数异或自身 = 0（a^a=0）；
2. 任何数异或 0 = 自身（a^0=a）；
3. 交换律和结合律（顺序不影响结果）；
遍历数组时，所有出现 2 次的数字会相互抵消为 0，最终结果即为只出现 1 次的数字。

3. 核心重点

空间优势：无需额外数据结构，空间复杂度 O (1)（比哈希表更优）；
时间复杂度：O (n)，仅需遍历一次数组；
适用场景：必须满足 "其余元素出现偶数次"，否则异或法失效。

方法 2：哈希集合（通用解）

1. 带注释代码

java

运行

java 复制代码

import java.util.HashSet;
import java.util.Set;

public class SingleNumberHashSet {
    public static void main(String[] args) {
        int[] nums = {4, 1, 2, 1, 2};
        System.out.println("只出现一次的数字：" + singleNumber(nums));
    }

    /**
     * 哈希集合求解：通用解（不限制其他元素出现次数）
     * @param nums 输入数组
     * @return 只出现一次的数字
     */
    public static int singleNumber(int[] nums) {
        Set<Integer> set = new HashSet<>(); // 哈希集合：存储已遍历的数字（add/removeO(1)）
        
        for (int num : nums) {
            // 若数字已在集合中，说明出现第2次，移除（抵消）
            if (set.contains(num)) {
                set.remove(num);
            } else {
                // 若不在集合中，说明首次出现，加入集合
                set.add(num);
            }
        }
        
        // 最终集合中仅剩"只出现一次的数字"（遍历取第一个元素）
        return set.iterator().next();
    }
}

2. 核心逻辑

利用哈希集合（HashSet）的「无重复元素」特性：
- 首次遇到数字：加入集合；
- 再次遇到数字：从集合中移除（抵消两次出现）；
遍历结束后，集合中仅剩余「只出现一次的数字」。

3. 核心重点

通用性：无需限制其他元素出现次数（比如出现 3 次也适用）；
数据结构选择：哈希集合（HashSet）比树集合（TreeSet）更优，因为 add/remove/contains 操作是 O (1)（TreeSet 是 O (logn)）；
空间复杂度：O (n)（最坏情况存储 n/2 +1 个元素）。

三、复制带随机指针的列表

方法 1：哈希表（简单易理解）

1. 带注释代码

java

运行

java 复制代码

import java.util.HashMap;
import java.util.Map;

// 定义带随机指针的链表节点
class Node {
    int val;
    Node next;
    Node random;
    Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}

public class CopyRandomListWithMap {
    public Node copyRandomList(Node head) {
        if (head == null) return null;
        
        // 哈希表：key=原节点，value=对应的新节点（建立原新节点映射）
        Map<Node, Node> nodeMap = new HashMap<>();
        
        // 第一步：遍历原链表，创建所有新节点（只复制val，不处理next和random）
        Node cur = head;
        while (cur != null) {
            nodeMap.put(cur, new Node(cur.val));
            cur = cur.next;
        }
        
        // 第二步：再次遍历原链表，通过哈希表映射，设置新节点的next和random
        cur = head;
        while (cur != null) {
            // 新节点的next = 原节点next对应的新节点
            nodeMap.get(cur).next = nodeMap.get(cur.next);
            // 新节点的random = 原节点random对应的新节点（若原random为null，映射后也为null）
            nodeMap.get(cur).random = nodeMap.get(cur.random);
            cur = cur.next;
        }
        
        // 返回新链表的头节点（原头节点对应的新节点）
        return nodeMap.get(head);
    }
}

2. 核心逻辑

分两步遍历：
1. 第一次遍历：仅创建新节点，用哈希表存储「原节点 → 新节点」的映射关系；
2. 第二次遍历：利用哈希表的 O (1) 查询特性，快速找到新节点的 next 和 random 指向（直接通过原节点的 next/random 取映射）。

3. 核心重点

难点突破：通过哈希表解决「新节点无法找到对应 random 节点」的问题；
时间复杂度：O (n)（两次遍历链表）；
空间复杂度：O (n)（哈希表存储 n 个节点映射）。

方法 2：不使用哈希表（作业要求，空间优化）

1. 带注释代码

java

运行

java 复制代码

public class CopyRandomListWithoutMap {
    public Node copyRandomList(Node head) {
        if (head == null) return null;
        
        // 第一步：在原节点后插入对应的新节点（原1→原2→原3 → 原1→新1→原2→新2→原3→新3）
        Node cur = head;
        while (cur != null) {
            Node newNode = new Node(cur.val); // 创建新节点（复制val）
            // 插入新节点到原节点和原next之间
            newNode.next = cur.next;
            cur.next = newNode;
            cur = newNode.next; // 跳过新节点，遍历下一个原节点
        }
        
        // 第二步：设置新节点的random指针（关键：利用原节点的random映射）
        cur = head;
        while (cur != null) {
            Node newNode = cur.next; // 新节点紧跟原节点
            // 原节点的random不为null → 新节点的random = 原random的下一个节点（即原random对应的新节点）
            // 原节点的random为null → 新节点的random也为null
            newNode.random = (cur.random != null) ? cur.random.next : null;
            cur = newNode.next; // 跳过新节点，遍历下一个原节点
        }
        
        // 第三步：拆分链表（分离原节点和新节点，得到独立的新链表）
        cur = head;
        Node newHead = head.next; // 新链表的头节点（原头节点的下一个）
        while (cur != null) {
            Node newNode = cur.next;
            cur.next = newNode.next; // 原节点指向原下一个节点（跳过新节点）
            // 新节点指向新下一个节点（若新节点是最后一个，则指向null）
            newNode.next = (newNode.next != null) ? newNode.next.next : null;
            cur = cur.next; // 遍历下一个原节点
        }
        
        return newHead;
    }
}

2. 核心逻辑

三步法（无需额外空间，利用原链表结构）：
1. 插入新节点：在每个原节点后插入对应的新节点，形成「原→新→原→新」的链表；
2. 设置 random：新节点的 random = 原节点 random 的下一个节点（因为原节点 random 后紧跟其对应的新节点）；
3. 拆分链表：将原节点和新节点分离，各自形成独立链表。

3. 核心重点

作业难点突破：
- 解决「找不到第三个节点 random」：通过「原节点 random → 新节点」的相邻关系，直接定位；
- 解决「跳跃式节点」：拆分时通过 newNode.next = newNode.next.next 跳过原节点，确保新链表连续；
空间优化：O (1)（仅用几个指针变量，无额外数据结构）；
时间复杂度：O (n)（三次遍历链表）；
注意事项：拆分时必须先处理原节点的 next，再处理新节点的 next，避免链表断裂。

四、宝石与石头

1. 带注释代码

java

运行

java 复制代码

import java.util.HashSet;
import java.util.Set;

public class NumJewelsInStones {
    public static void main(String[] args) {
        String jewels = "aA"; // 宝石类型（区分大小写）
        String stones = "aAAbbbb"; // 拥有的石头
        System.out.println("宝石数量：" + numJewelsInStones(jewels, stones));
    }

    /**
     * 统计石头中宝石的数量
     * @param jewels 宝石类型字符串（无重复字符）
     * @param stones 石头字符串
     * @return 宝石的总数量
     */
    public static int numJewelsInStones(String jewels, String stones) {
        // 哈希集合：存储宝石类型（查询O(1)，比TreeSet更优，因无需排序）
        Set<Character> jewelSet = new HashSet<>();
        for (char c : jewels.toCharArray()) {
            jewelSet.add(c);
        }
        
        int count = 0;
        // 遍历石头，判断每个字符是否是宝石
        for (char c : stones.toCharArray()) {
            if (jewelSet.contains(c)) {
                count++;
            }
        }
        return count;
    }
}

2. 核心逻辑

先将「宝石类型」存入哈希集合（利用 O (1) 查询特性）；
遍历「石头」字符串，逐个判断字符是否在宝石集合中，是则计数器累加。

3. 核心重点

数据结构选择：
- 哈希集合（HashSet）优于树集合（TreeSet）：宝石类型无需排序，HashSet 的 contains 是 O (1)，TreeSet 是 O (logk)（k 为宝石类型数）；
- 不适用 TreeMap：TreeMap 是键值对结构，且键需可比较，本题仅需判断 "是否存在"，集合更合适；
时间复杂度：O (m + n)（m 为宝石长度，n 为石头长度）；
边界处理：宝石为空则返回 0，石头为空则返回 0（集合 contains 天然兼容）。

五、坏键盘打字

1. 带注释代码

java

运行

java 复制代码

import java.util.HashSet;
import java.util.Set;

public class BrokenKeyboard {
    public static void main(String[] args) {
        String expected = "7_This_is_a_test"; // 应输入的字符串
        String actual = "_hs_s_a_es"; // 实际输入的字符串（大写已转换）
        System.out.println("坏键：" + findBrokenKeys(expected, actual));
    }

    /**
     * 找出坏键盘的键（不重复，按出现顺序输出）
     * @param expected 应输入的字符串
     * @param actual 实际输入的字符串
     * @return 坏键集合（大写）
     */
    public static String findBrokenKeys(String expected, String actual) {
        // 步骤1：将两个字符串统一转为大写（忽略大小写差异）
        String expectedUpper = expected.toUpperCase();
        String actualUpper = actual.toUpperCase();
        
        // 步骤2：将实际输入的字符存入哈希集合（查询O(1)）
        Set<Character> actualSet = new HashSet<>();
        for (char c : actualUpper.toCharArray()) {
            actualSet.add(c);
        }
        
        // 步骤3：遍历应输入字符串，找出"不在实际集合中且未记录的坏键"
        Set<Character> brokenKeys = new HashSet<>(); // 存储坏键（去重）
        StringBuilder result = new StringBuilder();
        
        for (char c : expectedUpper.toCharArray()) {
            // 条件：1. 实际输入中没有该字符；2. 未被记录为坏键
            if (!actualSet.contains(c) && !brokenKeys.contains(c)) {
                brokenKeys.add(c);
                result.append(c);
            }
        }
        
        return result.toString();
    }
}

2. 核心逻辑

统一大小写：避免因大小写差异导致误判；
哈希集合存储实际输入字符：快速判断 "应输入字符是否被实际输入"；
双重去重：用额外集合存储已发现的坏键，确保输出无重复。

3. 核心重点

大小写处理：必须先统一转换（题目隐含 "不区分大小写"，坏键按大写输出）；
去重关键：用 brokenKeys 集合记录已找到的坏键，避免重复添加；
时间复杂度：O (m + n)（m 为应输入长度，n 为实际输入长度）；
边界处理：实际输入为空 → 所有应输入字符都是坏键（需去重）。

六、前 k 个高频单词

1. 带注释代码

java

运行

java 复制代码

import java.util.*;

public class TopKFrequentWords {
    public static void main(String[] args) {
        String[] words = {"i", "love", "leetcode", "i", "love", "coding"};
        int k = 2;
        System.out.println("前" + k + "个高频单词：" + topKFrequent(words, k));
    }

    /**
     * 找出前k个高频单词（频率相同按字典序升序）
     * @param words 输入单词数组
     * @param k 前k个
     * @return 结果列表
     */
    public static List<String> topKFrequent(String[] words, int k) {
        // 第一步：用哈希表统计每个单词的出现频率（O(n)）
        Map<String, Integer> frequencyMap = new HashMap<>();
        for (String word : words) {
            frequencyMap.put(word, frequencyMap.getOrDefault(word, 0) + 1);
        }
        
        // 第二步：用优先队列（小根堆）筛选前k个高频单词（核心：自定义排序规则）
        // 堆的排序规则：
        // 1. 频率不同：频率小的在前（小根堆，优先弹出低频单词）
        // 2. 频率相同：字典序大的在前（弹出字典序大的，保留小的）
        PriorityQueue<String> minHeap = new PriorityQueue<>((a, b) -> {
            int freqA = frequencyMap.get(a);
            int freqB = frequencyMap.get(b);
            if (freqA != freqB) {
                return freqA - freqB; // 频率升序（小根堆）
            } else {
                return b.compareTo(a); // 字典序降序（频率相同时，大的先弹出）
            }
        });
        
        // 遍历哈希表，向堆中添加单词（O(m logk)，m为不同单词数）
        for (String word : frequencyMap.keySet()) {
            minHeap.offer(word);
            // 堆大小超过k时，弹出堆顶（低频或字典序大的单词），确保堆中是前k个
            if (minHeap.size() > k) {
                minHeap.poll();
            }
        }
        
        // 第三步：堆中元素逆置（堆顶是第k名，逆置后为1~k名）
        List<String> result = new ArrayList<>();
        while (!minHeap.isEmpty()) {
            result.add(minHeap.poll());
        }
        Collections.reverse(result); // 逆置后，高频在前，频率相同时字典序小的在前
        
        return result;
    }
}

2. 核心逻辑

统计频率：哈希表存储「单词→频率」；
小根堆筛选：
- 堆大小控制在 k，超过则弹出堆顶（确保堆中是当前前 k 高频）；
- 自定义排序规则：频率优先（小的先弹），频率相同则字典序大的先弹；
结果逆置：堆顶是第 k 名，逆置后得到「高频在前、字典序升序」的结果。

3. 核心重点

堆排序规则是关键：
- 为什么用小根堆？比大根堆更高效（O (m logk) vs O (m logm)），无需存储所有单词；
- 频率相同的处理：通过 b.compareTo(a) 让字典序大的单词先弹出，堆中保留字典序小的，最终逆置后满足要求；
时间复杂度：O (n + m logk)（n 为单词总数，m 为不同单词数，m ≤ n）；
边界处理：
- k 等于不同单词数 → 返回所有单词（按规则排序）；
- 所有单词频率相同 → 返回前 k 个字典序最小的单词。

数据结构===Map/Set （2）===

一，哈希表的核心基础概念（含底层逻辑，实例细节，边界情况）

1. 定义与核心思想（深入拆解）

2. 核心操作逻辑（含步骤拆解）

（1）插入操作（3 步）

（2）查找操作（3 步）

（3）删除操作（依赖冲突解决方式）

二、哈希冲突相关知识点（含本质原因与实例）

1. 哈希冲突的定义与相关概念（精准细化）

2. 冲突的必然性验证（实例量化）

三、避免哈希冲突的方法（冲突发生前，含底层原理）

1. 设计合理的哈希函数（含规则细节与实例推演）

（1）哈希函数的 3 条设计规则（逐条拆解）

（2）常见哈希函数类型（含公式、实例、优缺点全解析）

① 直接定制法

② 除留余数法（最常用）

③ 平方取中法（适用于短 Key）

④ 数学分析法（适用于 Key 有固定格式）

（3）实际开发使用原则（无例外）

2. 调节负载因子（含数学推导、Java 源码细节）

（1）负载因子的定义与数学表达

（2）负载因子与冲突率的定量关系

（3）调节负载因子的底层逻辑（数学推导）

（4）Java 中的负载因子与扩容机制（源码级细节）

① 核心参数

② 扩容实例推演

③ 扩容的关键步骤（rehash 过程）

④ 扩容的注意事项

四、解决哈希冲突的方法（冲突发生后，含代码级细节）

1. 闭散列（开放地址法）------ 冲突元素存入原数组

（1）线性探测（Linear Probing）

① 探测规则

② 完整实例推演

③ 核心问题：元素聚集（Clustering）

④ 删除问题与伪删除法（代码级实现）

（2）二次探测（Quadratic Probing）------ 解决聚集问题

① 探测规则（公式推导）

② 完整实例推演

③ 约束条件（插入成功的必要条件）

（1）结构细节（JDK8+ HashMap）

① 底层结构组成

② 哈希值扰动函数（减少冲突的关键）

（2）核心操作逻辑（以插入为例）

① 插入步骤（JDK8+ 尾插法）

② 实例推演（数组长度 n=16，α=0.75）

（4）开散列的优缺点

五、哈希表 与 Java 中的应用（ 代码案例）

一、统计单词个数

1. 带注释代码

2. 核心逻辑

3. 核心重点

二、只出现一次的数字

方法 1：异或运算（最优解）

1. 带注释代码

2. 核心逻辑

3. 核心重点

方法 2：哈希集合（通用解）

1. 带注释代码

2. 核心逻辑

3. 核心重点

三、复制带随机指针的列表

方法 1：哈希表（简单易理解）

1. 带注释代码

2. 核心逻辑

3. 核心重点

方法 2：不使用哈希表（作业要求，空间优化）

1. 带注释代码

2. 核心逻辑

3. 核心重点

四、宝石与石头

1. 带注释代码

2. 核心逻辑

3. 核心重点

五、坏键盘打字

1. 带注释代码

2. 核心逻辑

3. 核心重点

六、前 k 个高频单词

1. 带注释代码

2. 核心逻辑

五、哈希表与 Java 中的应用（代码案例）