【C++ 数据结构】二叉搜索树：原理、实现与核心操作全解析

作为 C++ 数据结构学习的重要章节，二叉搜索树（Binary Search Tree，简称 BST）是连接线性结构与高级平衡树的关键桥梁。它通过巧妙的节点排序规则，实现了高效的查找、插入和删除操作，是数据库索引、排序算法等场景的基础。本文将从概念定义出发，逐步拆解二叉搜索树的核心特性与实现细节，并基于一份完整的参考代码进行讲解，帮助大家构建完整的知识体系。

---

目录

一、二叉搜索树的核心概念

[1. 基本定义与特性](#1. 基本定义与特性)

[2. 结构优势与应用场景](#2. 结构优势与应用场景)

[3. 关键特性：中序遍历的有序性](#3. 关键特性：中序遍历的有序性)

二、二叉搜索树的完整代码实现

三、核心操作深度解析

[1. 插入操作 (Insert)](#1. 插入操作 (Insert))

[2. 中序遍历实现（验证有序性）](#2. 中序遍历实现（验证有序性）)

[3. 查找操作 (Find)](#3. 查找操作 (Find))

[4. 删除操作 (Erase)](#4. 删除操作 (Erase))

四、代码优化与注意事项

[1. 代码优化点](#1. 代码优化点)

[2. 常见错误与避坑指南](#2. 常见错误与避坑指南)

五、总结与进阶方向

[1. 二叉搜索树的优缺点](#1. 二叉搜索树的优缺点)

[2. 进阶学习方向](#2. 进阶学习方向)

---

一、二叉搜索树的核心概念

1. 基本定义与特性

二叉搜索树本质是一棵满足特定排序规则的二叉树，核心特性可概括为：

• 二叉树基础 ：每个节点最多有两个子节点（左子树left、右子树right）。
• 排序规则 ：
  • 左子树中所有节点的值 小于 根节点的值。
  • 右子树中所有节点的值 大于 根节点的值。
  • 递归特性：上述规则适用于树中任意子树（即每棵子树都是二叉搜索树）。
• 边界情况：叶子节点（无子女）天然满足定义，空树也可视为特殊的二叉搜索树。

结构示意图：

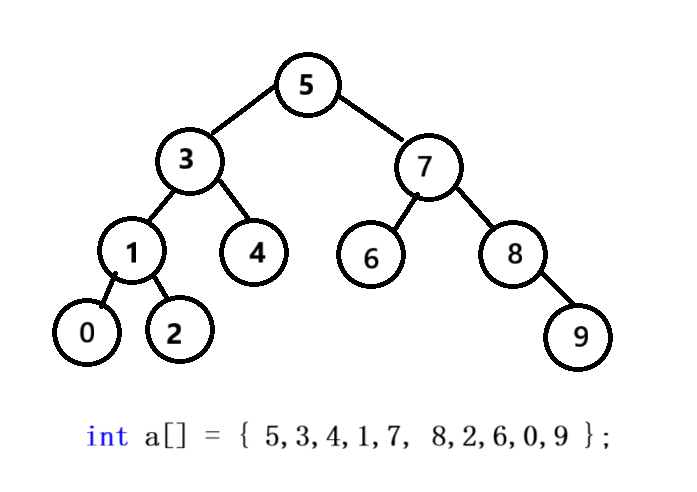
2. 结构优势与应用场景

相比顺序表、链表等线性结构，二叉搜索树的核心优势在于高效搜索：

• 线性结构查找时间复杂度为 O (n)，需遍历所有元素。
• 二叉搜索树通过 "比较 - 分支" 策略，每次可缩小一半搜索范围，理想情况下时间复杂度为 O (log n)（树的高度）。
• 典型应用：作为数据库索引的底层实现、动态数据的排序与查找、平衡树（AVL 树、红黑树）的基础结构。

3. 关键特性：中序遍历的有序性

二叉搜索树最核心的特性是：中序遍历（左 - 根 - 右）的结果是严格递增的有序序列。

• 示例：包含节点 {3,1,4,0,2,5} 的二叉搜索树，中序遍历结果为 [0,1,2,3,4,5]。
• 价值：无需额外排序操作，通过中序遍历即可获得有序数据，这也是其 "排序二叉树" 别名的由来。

二、二叉搜索树的完整代码实现

该代码时二叉搜索树的完整实现。这份代码结构清晰，包含了所有核心操作。接下来我们会围绕该实现讲解二叉搜索树。

#pragma once
#include <iostream>
using namespace std;
#include<assert.h>

template<class K>
struct BSTreeNode	//搜索二叉树
{
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;

	K _key;
	BSTreeNode(const K& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{}
};

template<class K>
class BSTree
{
	typedef	BSTreeNode<K> Node;
public:
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}
		Node* prev = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				prev = cur;
				cur = cur->_right;
			}else if(cur->_key > key)
			{
				prev = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(key);
		if (prev->_key < key)
			prev->_right = cur;
		else
			prev->_left = cur;
		return true;
	}
	void _InOder(Node* root)
	{
		if (root == nullptr)
			return ;
		_InOder(root->_left);
		cout<< root->_key << " ";
		_InOder(root->_right);
	}
	void InOder()
	{
		_InOder(_root);
		cout << endl;
	}
	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
				cur = cur->_left;
			else if (cur->_key < key)
				cur = cur->_right;
			else
				return true;
		}
		return false;
	}
	bool Erase(const K& key)
	{
		assert(_root != nullptr);
		/*if (_root->_key == key && _root->_left == nullptr && _root->_right == nullptr)
		{	
			delete _root;
			_root = nullptr;
			return true;
		}*/
		Node* prve = nullptr;
		Node* cur = _root;

		while (cur)
		{
			if (cur->_key < key)
			{
				prve = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				prve = cur;
				cur = cur->_left;
			}//找到了 开始删除
			else
			{
				//1 .左树为空
				//2 .右树为空
				//3 .左右树都不为空
				if (cur->_left == nullptr)
				{	//1.左为空 父亲指向我的右孩子
					if (cur == _root)  //如果删除的是根节点
					{
						_root = cur->_right; // 根节点指向其右子树
					}
					else
					{
						if (prve->_left->_key == cur->_key)
						{
							prve->_left = cur->_right;
						}
						else
						{
							prve->_right = cur->_right;
						}
					}
					delete cur;
				}
				else if (cur->_right == nullptr)
				{	//2.右为空 父亲指向我的左孩子
					if (cur == _root)  // 如果删除的是根节点
					{
						_root = cur->_left; // 根节点指向其左子树
					}
					else
					{
						if (prve->_left->_key == cur->_key)
						{
							prve->_left = cur->_left;
						}
						else
						{
							prve->_right = cur->_left;
						}
					}
					delete cur;
				}
				else
				{	//3.左右都不为空 不能直接删除 使用替换法删除
					//可以找左子树的最大节点（最右节点）或右子树的最小节点（最左节点）取替代他
					Node* rightMinPrev = nullptr;
					Node* rightMin = cur->_right;
					while (rightMin->_left)
					{
						rightMinPrev = rightMin;
						rightMin = rightMin->_left;
					}

					cur->_key = rightMin->_key;
					if (rightMinPrev == nullptr)
					{
						rightMinPrev = cur;
						rightMinPrev->_right = rightMin->_right;
					}
					else
					{
						rightMinPrev->_left = rightMin->_right;
					}

					delete rightMin;			
				}
				return true;
			}
		}
		return false;
	}
private:
	Node* _root = nullptr ;
};
//测试用例
void test()
{
	BSTree<int> t;
	int a[] = { 5,3,4,1,7, 8,2,6,0,9 };
	for (auto e : a)
	{
		t.Insert(e);
	}
	t.InOder();
	cout<<t.Find(1)<<endl;
	//1.叶子
	t.Erase(7);
	t.InOder();
	//1.左或右为空
	t.Erase(8);
	t.Erase(1);
	t.InOder();
	//3.左右都不为空
	t.Erase(5);
	t.InOder();

	BSTree<int> t2;
	int b[] = { 5,3,4,1,7, 8,2,6,0,9 };
	for (auto e : b)
	{
		t2.Insert(e);
	}
	t2.InOder();
	for (auto e : b)
	{
		t2.Erase(e);
		t2.InOder();
	}

三、核心操作深度解析

1. 插入操作 (Insert)

• 核心思想：找到合适的叶子节点位置，遵循 BST 规则插入。
• 步骤：

1.如果树为空，直接创建根节点。

bool Insert(const K& key)
{
	if (_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}
//2.否则，从根节点出发，根据关键字大小遍历，找到插入点（cur为空时的parent位置）。
//3.创建新节点，并根据关键字大小将其链接为parent的左孩子或右孩子。	
}

2.否则，从根节点出发，根据关键字大小遍历，找到插入点（cur为空时的parent位置）。

bool Insert(const K& key)
{
//1.如果树为空，直接创建根节点。

    if (_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}
	Node* prev = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < key)
		{
			prev = cur;
			cur = cur->_right;
		}else if(cur->_key > key)
		{
			prev = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}
//3.创建新节点，并根据关键字大小将其链接为parent的左孩子或右孩子。
	
}

3.创建新节点，并根据关键字大小将其链接为parent的左孩子或右孩子。

bool Insert(const K& key)
{
	if (_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}
	Node* prev = nullptr;    //使用prev(parent指针记录父节点，是链接新节点的关键。
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < key)
		{
			prev = cur;
			cur = cur->_right;
		}else if(cur->_key > key)
		{
			prev = cur;
			cur = cur->_left;
		}
		else
		{
			return false;  //不允许插入重复值，找到重复值时直接返回false。
		}
	}
	cur = new Node(key);
	if (prev->_key < key)
		prev->_right = cur;
	else
		prev->_left = cur;
	return true;
}

• 关键点 ：
  • 使用parent指针记录父节点，是链接新节点的关键。
  • 不允许插入重复值，找到重复值时直接返回false。

2. 中序遍历实现（验证有序性）

中序遍历是验证二叉搜索树正确性的重要工具，这里实现递归版（简洁直观）：

	void _InOder(Node* root)
	{
		if (root == nullptr)
			return ;
		_InOder(root->_left);
		cout<< root->_key << " ";
		_InOder(root->_right);
	}
	void InOder()
	{
		_InOder(_root);
		cout << endl;
	}

3. 查找操作 (Find)

• 核心思想：利用 BST 的排序特性，进行二分查找。
• 步骤 ：
  1. 从根节点开始。
  2. 如果目标值大于当前节点值，向右子树查找；如果小于，向左子树查找。
  3. 如果相等，查找成功；如果遍历到空节点，查找失败。
• 时间复杂度：O (h)，h 为树的高度。在平衡树中 h≈log n，在最坏的情况下（树退化为链表）h=n。

bool Find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key > key)
			cur = cur->_left;
		else if (cur->_key < key)
			cur = cur->_right;
		else
			return true;
	}
	return false;
}

4. 删除操作 (Erase)

删除操作是 BST 中最复杂的，因为删除一个节点后，必须保证树的 BST 性质不被破坏。处理方式取决于待删除节点的子节点情况：

• 情况 1：左子树为空

  • 直接将待删除节点的父节点指向其右子节点。
  • 如果待删除节点是根节点，则根节点更新为其右子节点。

• 情况 2：右子树为空

  • 直接将待删除节点的父节点指向其左子节点。
  • 如果待删除节点是根节点，则根节点更新为其左子节点。

• 情况 3：左右子树都不为空（重点）

  • 问题：不能简单地将父节点指向其中一个子树，因为这会丢失另一个子树的信息。
  • 解决方案（替换法） ：
    1. 找到待删除节点的右子树中的最小值节点 （或左子树中的最大值节点）。这个节点的特点是：它的左子树一定为空（或右子树一定为空），所以删除它很简单。
    2. 将这个 "替代节点" 的值复制到待删除节点的位置。
    3. 从树中删除这个 "替代节点"。
  • 好处：既删除了目标值，又保证了 BST 的性质，且操作只需要 O (h) 时间。

bool Erase(const K& key)
{
	assert(_root != nullptr);
	/*if (_root->_key == key && _root->_left == nullptr && _root->_right == nullptr)
	{	
		delete _root;
		_root = nullptr;
		return true;
	}*/
	Node* prve = nullptr;
	Node* cur = _root;

	while (cur)
	{
		if (cur->_key < key)
		{
			prve = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			prve = cur;
			cur = cur->_left;
		}//找到了 开始删除
		else
		{
			//1 .左树为空
			//2 .右树为空
			//3 .左右树都不为空
			if (cur->_left == nullptr)
			{	//1.左为空 父亲指向我的右孩子
				if (cur == _root)  //如果删除的是根节点
				{
					_root = cur->_right; // 根节点指向其右子树
				}
				else
				{
					if (prve->_left->_key == cur->_key)
					{
						prve->_left = cur->_right;
					}
					else
					{
						prve->_right = cur->_right;
					}
				}
				delete cur;
			}
			else if (cur->_right == nullptr)
			{	//2.右为空 父亲指向我的左孩子
				if (cur == _root)  // 如果删除的是根节点
				{
					_root = cur->_left; // 根节点指向其左子树
				}
				else
				{
					if (prve->_left->_key == cur->_key)
					{
						prve->_left = cur->_left;
					}
					else
					{
						prve->_right = cur->_left;
					}
				}
				delete cur;
			}
			else
			{	//3.左右都不为空 不能直接删除 使用替换法删除
				//可以找左子树的最大节点（最右节点）或右子树的最小节点（最左节点）取替代他
				Node* rightMinPrev = nullptr;
				Node* rightMin = cur->_right;
				while (rightMin->_left)
				{
					rightMinPrev = rightMin;
					rightMin = rightMin->_left;
				}

				cur->_key = rightMin->_key;
				if (rightMinPrev == nullptr)
				{
					rightMinPrev = cur;
					rightMinPrev->_right = rightMin->_right;
				}
				else
				{
					rightMinPrev->_left = rightMin->_right;
				}

				delete rightMin;			
			}
			return true;
		}
	}
	return false;
}

四、代码优化与注意事项

1. 代码优化点

• Erase函数中的断言 ：原代码中的assert(_root != nullptr);可以去掉。因为当树为空时，Find操作会直接返回false，Erase函数也应该能优雅地处理这种情况，而不是强制终止程序。
• Erase函数中判断父子关系 ：原代码中 if (prve->_left->_key == cur->_key) 的方式是错误且危险 的。如果prve->_left是nullptr，这会导致程序崩溃。正确的做法是直接比较指针，即 if (prve->_left == cur)。
• 代码风格 ：统一了变量命名（如prve改为parent），添加了更详细的注释，使代码更具可读性。

2. 常见错误与避坑指南

• 指针悬空 ：删除节点后，一定要将相关的指针置nullptr（虽然在本代码的逻辑中不是必须的，但这是一个非常好的编程习惯，可以防止后续代码误用悬空指针）。
• 父节点指针处理错误：在删除操作中，正确判断待删除节点是父节点的左孩子还是右孩子是关键。错误的判断会导致树的结构损坏。
• 根节点的特殊处理：由于根节点没有父节点，在插入（空树）和删除（根节点本身）时都需要进行特殊处理。
• 内存泄漏 ：new出来的节点，在Erase时一定要用delete释放，否则会造成内存泄漏。

五、总结与进阶方向

1. 二叉搜索树的优缺点

• 优点 ：
  • 实现简单，核心操作逻辑清晰。
  • 对于动态数据集合，插入、删除、查找的平均时间复杂度为 O (log n)。
  • 中序遍历可直接获得有序数据。
• 缺点 ：
  • 性能高度依赖于树的形态。在最坏情况下（如插入有序数据），树会退化成链表，所有操作的时间复杂度退化为 O (n)。
  • 缺乏自平衡能力。

2. 进阶学习方向

为了解决二叉搜索树的平衡问题，后续可以学习：

• AVL 树：一种严格平衡的二叉搜索树，通过旋转操作维持树的平衡，保证 O (log n) 的时间复杂度。
• 红黑树 ：一种近似平衡的二叉搜索树，通过颜色规则和旋转操作维持平衡，插入和删除的平均性能更好，是 C++ STL 中set、map等容器的底层实现。
• B 树 / B + 树：多路搜索树，更适合磁盘等外存储设备，是数据库索引的核心数据结构。

掌握好二叉搜索树是学习所有高级树结构的基础。希望这篇文章和优化后的代码能帮助你更好地理解和实现二叉搜索树。

希望这篇文章对你有帮助，如果你有任何问题或建议，欢迎在评论区留言。谢谢阅读！