【C语言&数据结构】二叉树的链式递归

二叉树的链式结构

一、二叉树的链式结构
二、实现链式二叉树

一、二叉树的链式结构

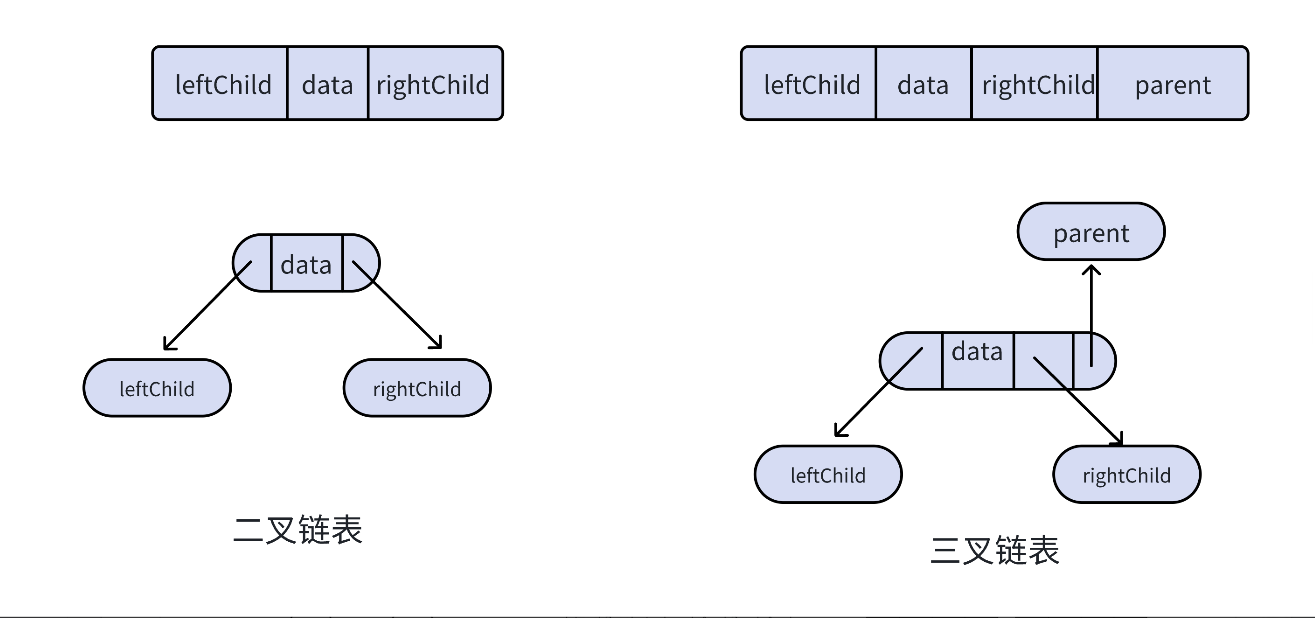
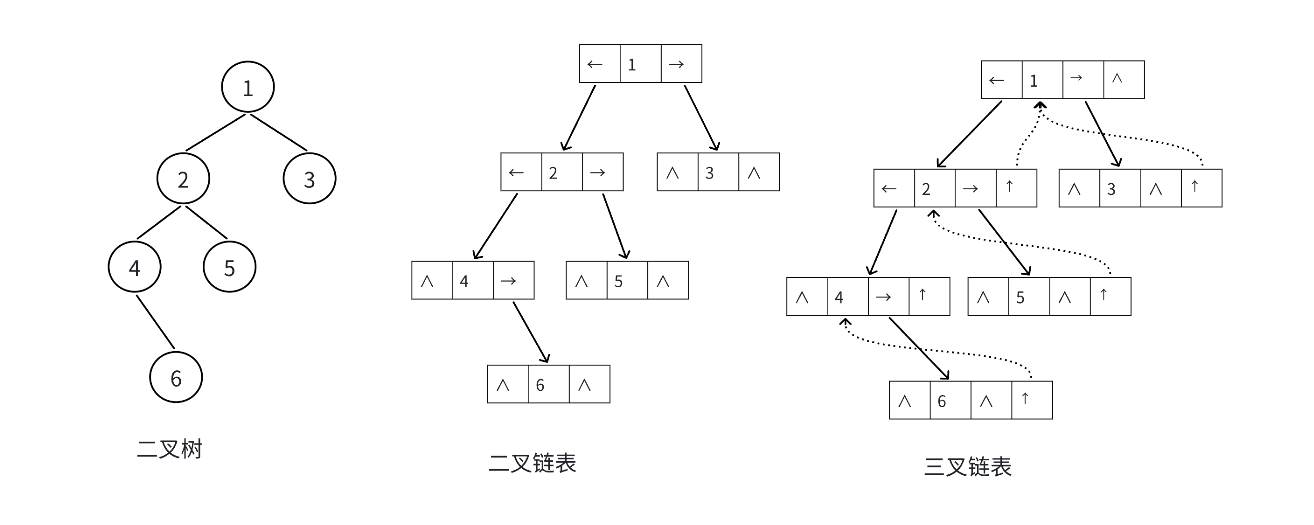
二叉树也可以用链表。通常由数据域和左右指针域 ，左右指针域表示左孩子和右孩子所在的链节点的存储地址 。链式结构又分为二叉链和三叉链，大部分都是二叉链。

二、实现链式二叉树

1.链式二叉树的定义

用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址，其结构如下：

C 复制代码

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>

typedef int BTDataType;

//二叉链
typedef struct BinaryTreeNode
{
	BTDataType Data;              //数据域
	struct BInaryTreeNode* left;  //指向当前左孩子节点
	struct BInaryTreeNode* right; //指向当前右孩子节点
}BTNode;

2.链式二叉树的创建

C 复制代码

//返回节点的地址，方便创建二叉树的节点
BTNode* BuyNode(int x);

C 复制代码

//返回节点的地址，方便创建二叉树的节点
BTNode* BuyNode(int x)
{
	//给节点申请空间
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return;
	}
	newnode->Data = x;
	newnode->left = NULL;
	newnode->right = NULL;

	//返回节点地址
	return newnode;
}

3.链式二叉树的形成

C 复制代码

//返回第一个节点的地址，创建其他子树的节点
BTNode* CreatBinaryTree();

C 复制代码

//返回第一个节点的地址，创建其他子树的节点
BTNode* CreatBinaryTree()
{
	//创建每个节点、并赋值
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	BTNode* node7 = BuyNode(7);
	BTNode* node8 = BuyNode(8);

	//形成一棵树
	node1->left = node2;
	node1->right = node5;
	node2->left = node3;
	node2->right = node4;
	node5->left = node6;
	node5->right = node7;
	node6->left = node8;

	//返回首节点为
	return node1;
}

4.前中后序遍历

二叉树的操作离不开树的遍历

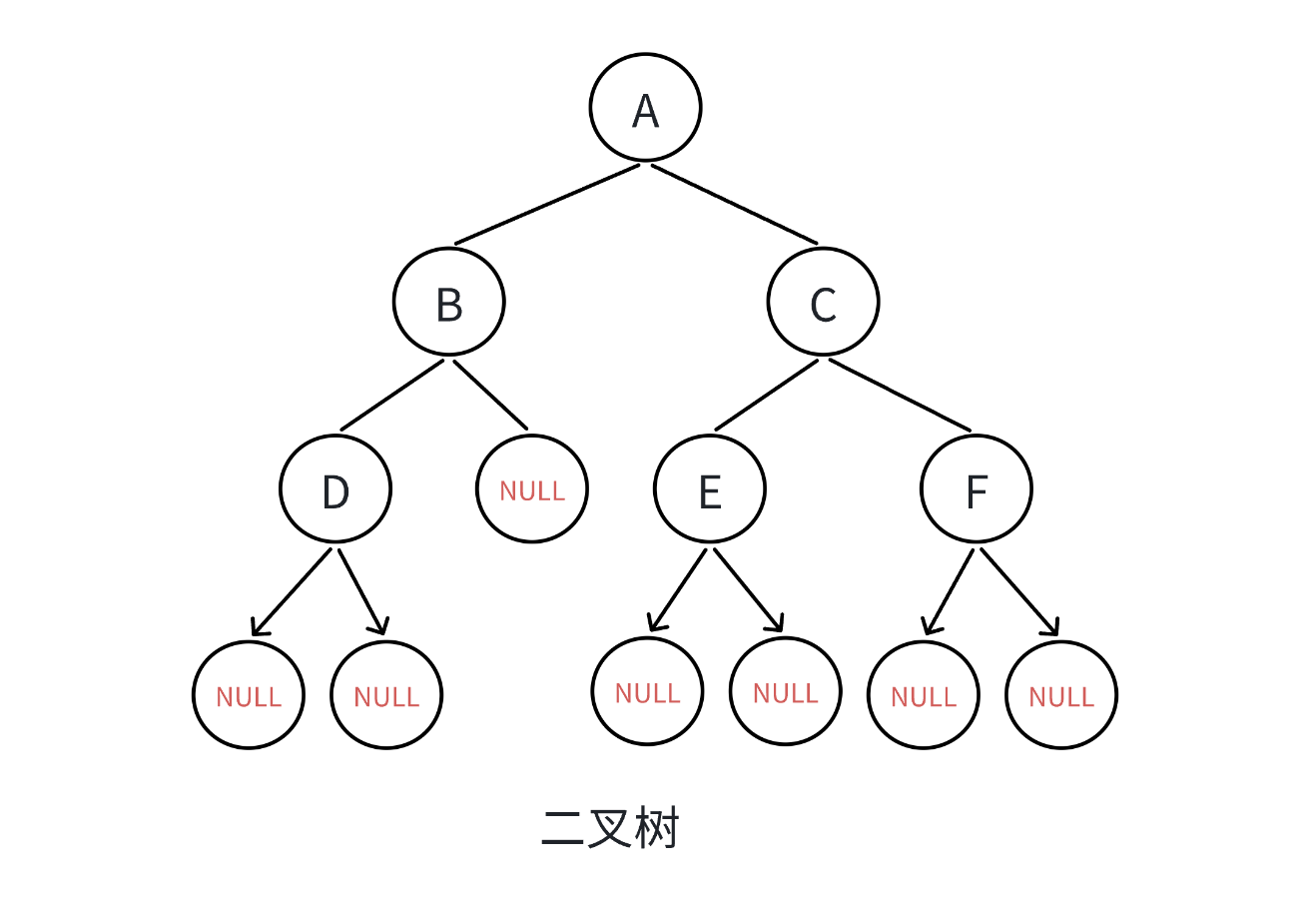
(1)遍历规则

按照规则，二叉树的遍历分为：前序/中序/后序的递归结构遍历：

前序遍历：访问根节点的操作发生在遍历其左右子树之前

访问顺序为：根节点、左子树、右子树

中序遍历：访问根节点的操作发生在遍历其左右子树之间

访问顺序为：左子树、根节点、右子树

后序遍历：访问根节点的操作发生在遍历其左右子树之后

访问顺序为：左子树、右子树、根节点

(2)链式二叉树的前序

C 复制代码

//前序遍历   根节点、左子树、右子树
void prevorder(BTNode* root);

C 复制代码

//前序遍历   根节点、左子树、右子树
void prevorder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	printf("%d ", root->Data);
	prevorder(root->left);
	prevorder(root->right);
}

(3)链式二叉树的中序

C 复制代码

//中序遍历   左子树、根节点、右子树
void inorder(BTNode* root);

C 复制代码

//中序遍历   左子树、根节点、右子树
void inorder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	prevorder(root->left);
	printf("%d ", root->Data);
	prevorder(root->right);
}

(4)链式二叉树的后序

C 复制代码

//后序遍历   左子树、右子树、根节点
void tailorder(BTNode* root);

C 复制代码

//后序遍历   左子树、右子树、根节点
void tailorder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	prevorder(root->left);
	prevorder(root->right);
	printf("%d ", root->Data);
}

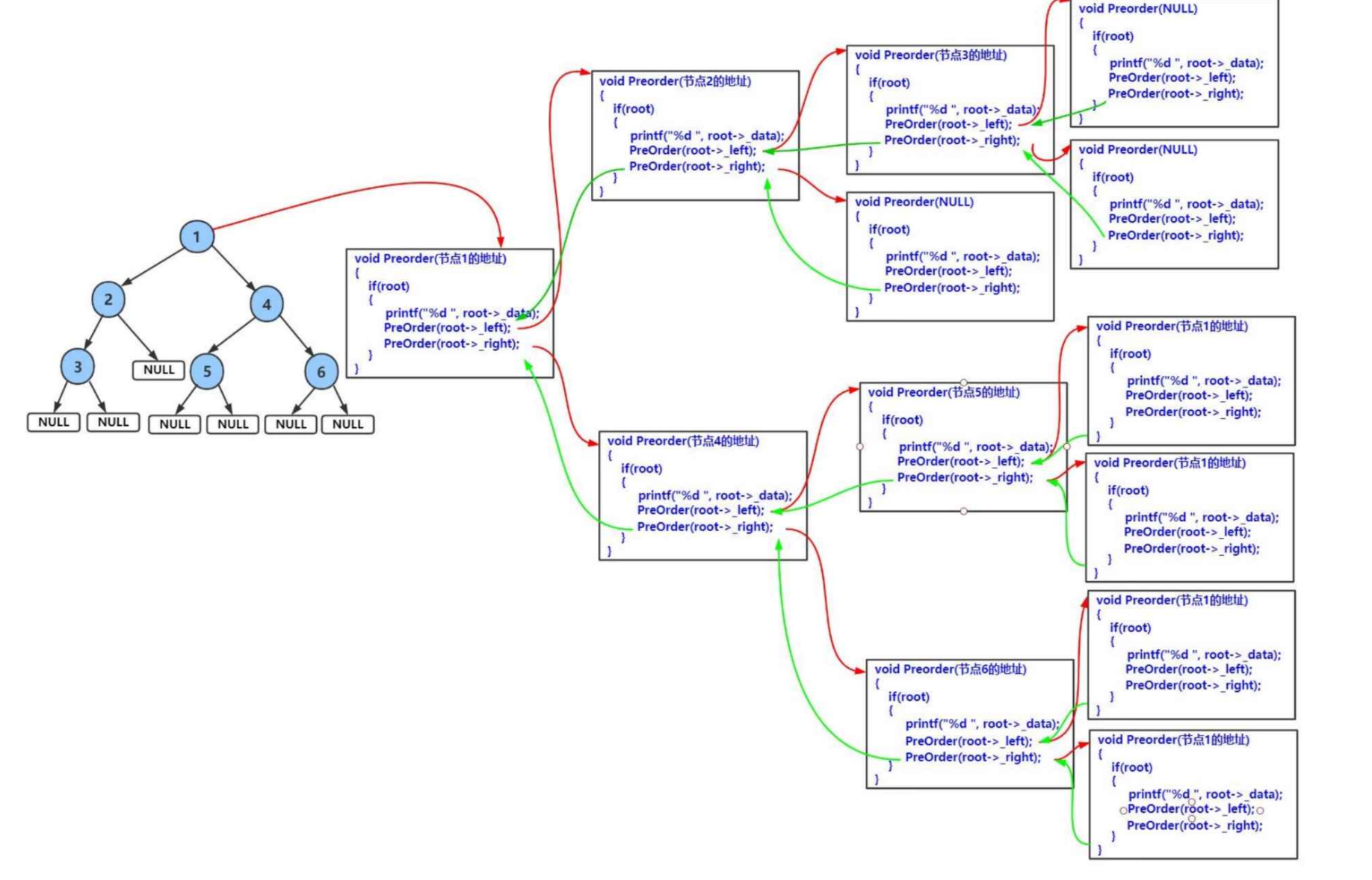
图解遍历：

以前序遍历为例：

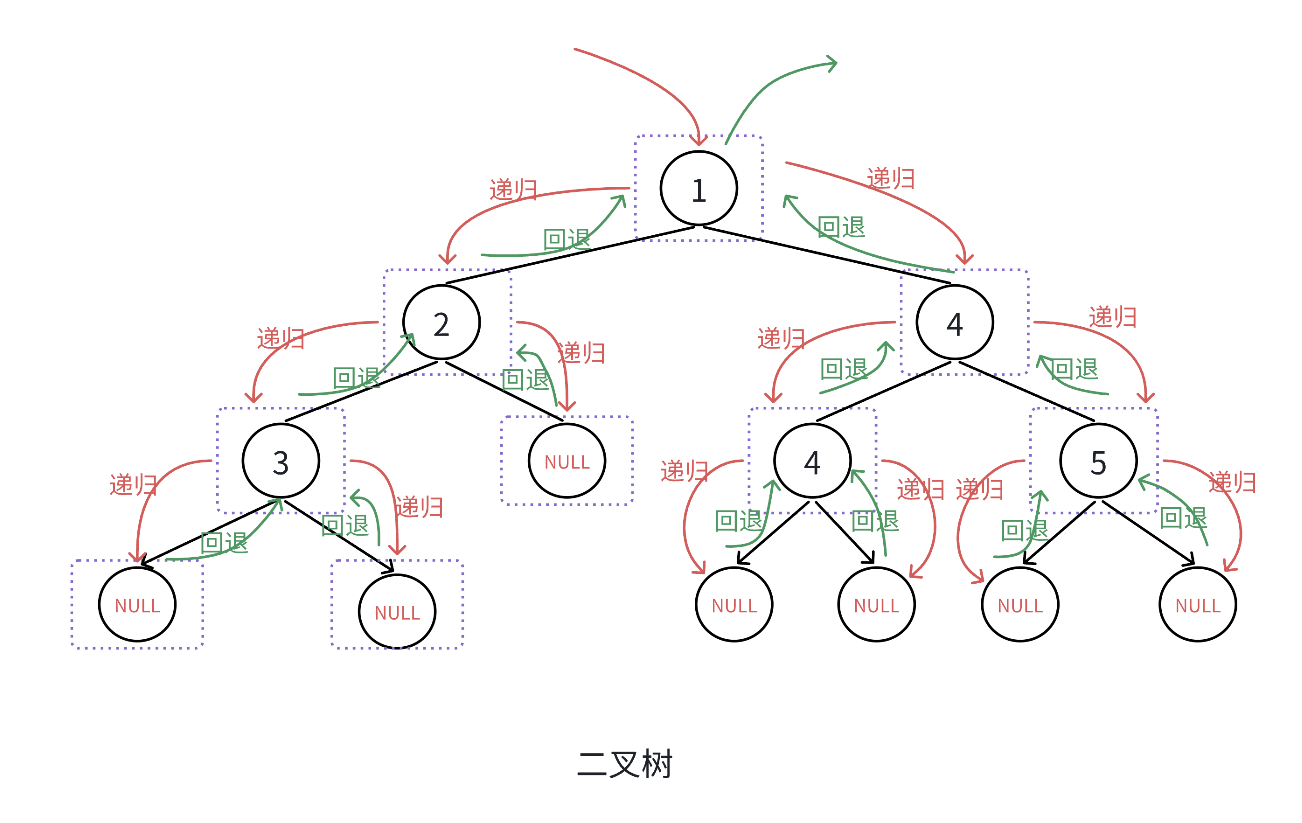
函数递归栈帧图：

5.链式二叉树节点个数

需用递归遍历二叉树

C 复制代码

//查找二叉树节点
int TreeSize(BTNode* root);

C 复制代码

//查找二叉树节点
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

6.链式二叉树的叶子个数

先判断树是否为空，然后需用条件语句判断两边是否是是空，然后用递归循环遍历

C 复制代码

//查找二叉树叶子节点
int TreeLeafSize(BTNode* root);

C 复制代码

//查找二叉树叶子节点
int TreeLeafSize(BTNode* root)
{
	//树为空
	if (root == NULL)
		return 0;
	
	//叶子节点，返回1
	if (root->left == NULL && root->right == NULL)
		return 1;

	//找不到，遍历二叉树
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

7.链式二叉树高度

先判断树是否为空，然后左子树往左递归，右子树往右递归，然后比较大小

C 复制代码

//查找二叉树高度
int TreeHeight(BTNode* root);

C 复制代码

//查找二叉树高度
int TreeHeight(BTNode* root)
{
	//树为空，高度为1
	if (root == NULL)
		return 1;

	//递归遍历，记录树两边的高度
	int leftcount = TreeHeight(root->left);
	int rightcount = TreeHeight(root->right);
	
	//比较两边高度(三目运算符)
	return 1 + (leftcount > rightcount ? leftcount : rightcount);
}

8.链式二叉树查找第K层节点个数

先判断树是否为空，再设一个K变量，遍历一次k--，直到k不满足条件退出循环为止

C 复制代码

//查找第K层的节点个数
int TreeLeveKSize(BTNode* root, int k);

C 复制代码

//查找第K层的节点个数
int TreeLeveKSize(BTNode* root, int k)
{
	//树为空
	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	//子问题
	return TreeLeveKSize(root->left, k - 1) + TreeLeveKSize(root->right, k - 1);
}

9.链式二叉树查找值为x的节点

先判断树是否为空，再遍历二叉树，用条件语句判断节点是否为x，为x则返回当前节点

C 复制代码

//二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x);

C 复制代码

//二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	//树为空/子树左孩子为空
	if (root == NULL)
		return NULL;

	//找到节点
	if (root->Data == x)
		return root;

	//没找到，往左子树找
	BTNode* ret1 = TreeFind(root->left, x);
	if (ret1)
		return ret1;

	//左子树没找到，往右子树找
	BTNode* ret2 = TreeFind(root->right, x);
	if (ret2)
		return ret2;

	//都没找到返回NULL
	return NULL;
}

10.链式二叉树的销毁

先判断树是否为空，再用递归遍历二叉树，利用后序销毁节点，防止先把节点销毁找不到子树

C 复制代码

//二叉树的销毁
void TreeDestory(BTNode* root);

C 复制代码

//二叉树的销毁
void TreeDestory(BTNode* root)
{
	if (root == NULL)
		return;

	//递归销毁
	TreeDestory(root->left);
	TreeDestory(root->right);
	free(root);
}

11.链式二叉树的广度遍历

需要用到队列(先进先出)，把第一个节点放入队列，把第一个节点拿出来，然后再把子树的两个节点放入队列里。把第二个节点拿出来，然后把子树的两个几点放入队列里，用递归循环往复即可(当在队列拿出节点时，需要把第一个节点存在另一颗树中)

需要在文件中，找到之前写的队列，复制粘贴到二叉树的文件中，然后再添加队列的头文件和源文件

C 复制代码

#include"Queue.h"

typedef struct BinaryTreeNode* QDataType;

注意：

包含头文件时，需要在Queue.h中，将typedef int QDataType修改成typedef struct BinaryTreeNode* QDataType

C 复制代码

//层序遍历(广度优先遍历)
void TreeLevelOrder(BTNode* root);

C 复制代码

#include"Queue.h"
//层序遍历(广度优先遍历)
void TreeLevelOrder(BTNode* root)
{
	//定义一个队列
	Queue q;
	QueueInit(&q);

	//如果树不等于空，就把树放进去
	if (root)
		QueuePush(&q, root);

	//如果队列不等于空就继续
	//当等于空时，树的节点走完
	while (!QueueEmpty(&q))
	{
		//保存树节点的指针
		BTNode* front = QueueFront(&q);
		QueuePop(&q);//取出来就要拿出来

		printf("%d ", front->Data);

		//然后把两个子树放进去
		if (front->left)
			QueuePush(&q, front->left);

		if (front->right)
			QueuePush(&q, front->right);
	}

	//用完则销毁队列
	QueueDestroy(&q);
}```