面试150——区间

并集

合并区间思路

合并区间是区间间取并集，最终返回所有的并集。按照左端点升序排序，不断更新右端点最大值，直到无法更新，则开新区间。
代码

class Solution {
    public int[][] merge(int[][] intervals) {
        int n = intervals.length;
        if (n == 0) return new int[0][0];
        Arrays.sort(intervals, (a, b)->(a[0] - b[0]));
        List<int[]> list = new ArrayList<>();
        for (int i = 0; i < n; i ++) {
            if (i == 0 || list.getLast()[1] < intervals[i][0]) {
                list.add(new int[] {intervals[i][0], intervals[i][1]}); // 没去可以合并的区间，则开新区间
            } else {
                list.getLast()[1] = Math.max(list.getLast()[1], intervals[i][1]); // 合并区间
            }
        }
        return list.toArray(new int[list.size()][2]);
    }
}

交集

交集思路

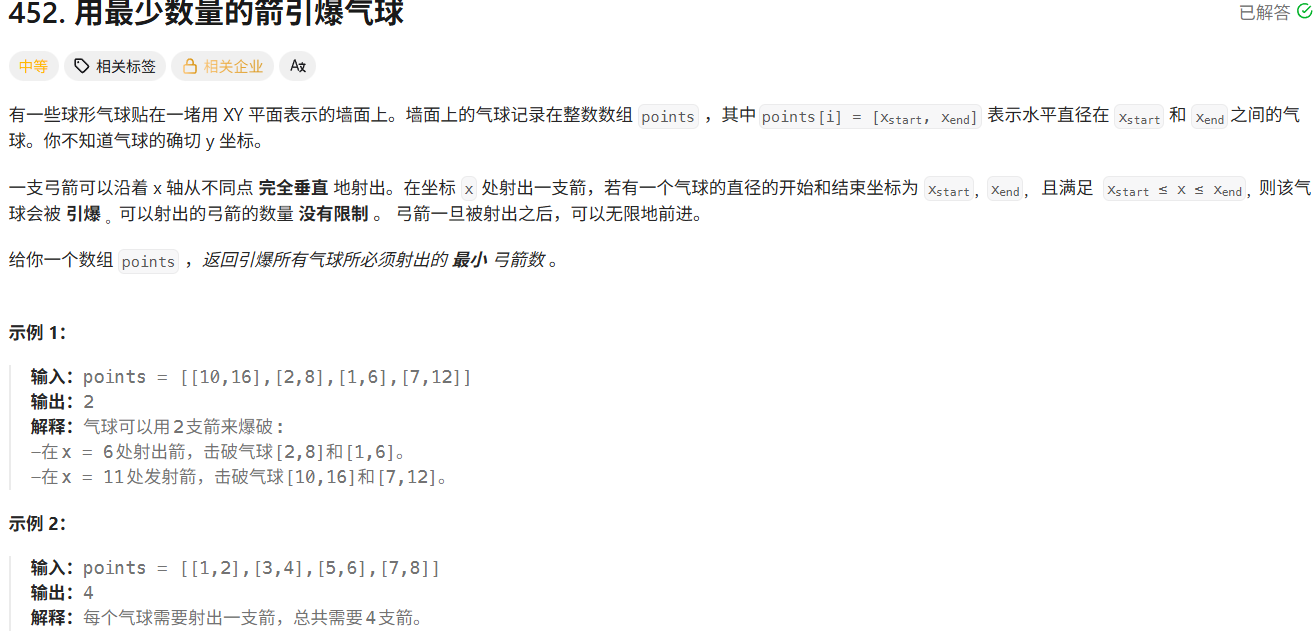
每次射都要射相交的部分，要使用的箭最少。则找到所有区间最少得相交的划分。每个区间在所有区间尽可能囊括多的有公共部分的区间，则这个区间的右边要大于囊括区间的左边。一种贪心的思路，右边越短的，希望囊括右边越短的。所以将右边按照升序排序。
代码

// 每次射希望能够射得最多，也就是每次找到重叠最多的气球
// 重叠部分是由一段区间最早结束的部分能覆盖多少决定的，所以按照区间右端点排序
class Solution {
    public int findMinArrowShots(int[][] points) {
        if (points == null) return 0;
        int n = points.length;
        if (n == 0) return 0;
        Arrays.sort(points, (a, b) -> Integer.compare(a[1], b[1]));
        int res = 0, right = 0;
        for (int i = 0; i < n; i ++) {
            if (i == 0 || right < points[i][0]) {
                res ++;
                right = points[i][1];
            }
        }
        return res;
    }
}