目录
[1. 引言:分类问题的直觉理解](#1. 引言:分类问题的直觉理解)
[1.1 什么是分类问题?](#1.1 什么是分类问题?)
[1.2 不同分类器的比较](#1.2 不同分类器的比较)
[2. 最大间隔原理:直观理解](#2. 最大间隔原理:直观理解)
[2.1 什么是最佳决策边界?](#2.1 什么是最佳决策边界?)
[1. 分类准确性](#1. 分类准确性)
[2. 泛化能力](#2. 泛化能力)
[3. 鲁棒性](#3. 鲁棒性)
[3. 数学基础:从几何到优化](#3. 数学基础:从几何到优化)
[3.1 决策超平面的数学表示](#3.1 决策超平面的数学表示)
[3.2 函数间隔和几何间隔](#3.2 函数间隔和几何间隔)
[3.3 最大间隔的数学形式化](#3.3 最大间隔的数学形式化)
[4. 支持向量的概念](#4. 支持向量的概念)
[4.1 什么是支持向量?](#4.1 什么是支持向量?)
[4.2 支持向量的重要性](#4.2 支持向量的重要性)
[5. 硬间隔SVM的数学推导](#5. 硬间隔SVM的数学推导)
[5.1 优化问题形式化](#5.1 优化问题形式化)
[5.2 拉格朗日对偶问题](#5.2 拉格朗日对偶问题)
[5.3 KKT条件](#5.3 KKT条件)
[6. 软间隔SVM:处理非线性可分数据](#6. 软间隔SVM:处理非线性可分数据)
[6.1 为什么需要软间隔?](#6.1 为什么需要软间隔?)
[6.2 松弛变量的引入](#6.2 松弛变量的引入)
[7. 核方法:处理非线性问题](#7. 核方法:处理非线性问题)
[7.1 线性不可分问题](#7.1 线性不可分问题)
[7.2 核技巧](#7.2 核技巧)
[8. SVM实践指南](#8. SVM实践指南)
[8.1 如何选择核函数](#8.1 如何选择核函数)
[8.2 参数调优策略](#8.2 参数调优策略)
[9. SVM的优缺点总结](#9. SVM的优缺点总结)
[9.1 优点](#9.1 优点)
[9.2 缺点](#9.2 缺点)
[9.3 适用场景](#9.3 适用场景)
[10. 学习路径建议](#10. 学习路径建议)
[10.1 循序渐进的学习步骤](#10.1 循序渐进的学习步骤)
1. 引言:分类问题的直觉理解
1.1 什么是分类问题?
想象你在纸上画了一些红色和蓝色的点,现在需要画一条线把这些点分开:
-
目标:找到一条"最好"的分界线
-
挑战:可能有很多条线都能分开这些点,哪条才是最好的?
例子:区分猫和狗的照片
-
每个照片可以用多个特征表示(大小、颜色、耳朵形状等)
-
我们需要在特征空间中找到决策边界
1.2 不同分类器的比较
|-------|--------|-------|--------|
| 分类器类型 | 决策边界 | 优点 | 缺点 |
| 最近邻 | 局部决策 | 简单直观 | 对噪声敏感 |
| 决策树 | 轴平行边界 | 可解释性强 | 容易过拟合 |
| 逻辑回归 | 线性边界 | 概率输出 | 只能线性分类 |
| 支持向量机 | 最大间隔边界 | 泛化能力强 | 计算复杂度高 |
2. 最大间隔原理:直观理解
2.1 什么是最佳决策边界?
问题的本质:分类的不确定性
想象你在管理两个敌对国家的边境线,你需要划出一条分界线:
-
糟糕的边界:紧挨着某个国家的城镇,任何小冲突都会波及平民
-
良好的边界:在两个国家之间建立缓冲区,减少冲突风险
在机器学习中,决策边界就是这条"分界线",而间隔(margin)就是"缓冲区"。
关键洞察:什么定义了"最佳"?
最佳决策边界由三个关键因素决定:
1. 分类准确性
-
必须正确分类训练数据(对于硬间隔SVM)
-
或最小化分类错误(对于软间隔SVM)
2. 泛化能力
-
边界应该远离数据点,创建"安全区域"
-
对新样本的分类更加可靠
3. 鲁棒性
-
对数据中的小噪声不敏感
-
对特征的小变化具有稳定性
数学视角:最大间隔的形式化定义
让我们从数学上精确理解什么是"最佳":
候选决策边界1:
方程: 1·x₁ + 1·x₂ + (-5) = 0
最小间隔: 0.000
候选决策边界2:
方程: 1·x₁ + 1·x₂ + (-7) = 0
最小间隔: 1.414
📌 关键观察:
边界2的最小间隔更大,因此是更好的选择
SVM的目标就是找到这样的边界:最大化最小间隔
🎯 最优性条件:
• 1. 所有数据点都被正确分类
• 2. 距离边界最近的点(支持向量)到边界的距离最大
• 3. 边界正好位于两个类别的中间位置现实世界类比:理解最大间隔的直觉
类比1:道路中线
想象你在画一条双向道路的中线:
-
差的画法:线紧挨着某条车道,车辆容易越线
-
好的画法:线在道路正中央,两边都有缓冲区
-
最佳画法:在中央画双黄线,创建最大的安全区域
类比2:法庭判决
在刑事审判中:
-
有罪/无罪就像二分类问题
-
证据强度就像点到决策边界的距离
-
合理怀疑就是间隔缓冲区
-
最佳判决:只有证据远超合理怀疑(大间隔)时才判有罪
可视化:支持向量的关键作用
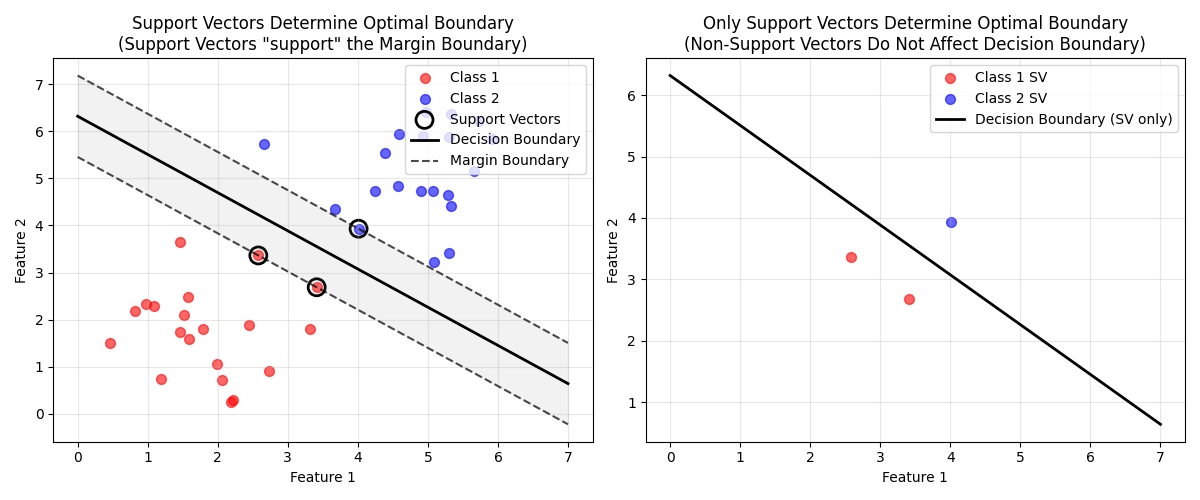
最佳决策边界的严格定义
基于以上分析,我们可以给出最佳决策边界的完整定义:
最佳决策边界是在满足分类约束的前提下,能够最大化训练数据中最近点到边界距离的那个超平面。
数学表达:
对于线性可分的训练集 {(xi,yi)}{(xi,yi)},其中 yi∈{−1,+1}yi∈{−1,+1},最佳决策边界是解决以下优化问题的解:
maxw,bγ满足yi(wTxi+b)≥γ,i=1,...,m∥w∥=1w,bmaxγ满足yi(wTxi+b)≥γ,i=1,...,m∥w∥=1
其中 γγ 是几何间隔。
为什么最大间隔是最佳的?统计学习理论解释
根据统计学习理论的VC维分析:
-
间隔越大 → VC维越小:大间隔意味着假设空间更简单
-
VC维越小 → 泛化误差界越紧:理论保证更好的泛化性能
-
结构风险最小化:SVM自动在经验风险和模型复杂度之间权衡
根据VC理论,泛化误差的上界为:
R(h) ≤ R_emp(h) + Φ(VC维, 样本数, 置信度)对于间隔为ρ的SVM:
• 有效VC维 ~ (R/ρ)²,其中R是数据范围
• 间隔ρ越大,VC维越小
• VC维越小,泛化误差上界越紧📊 实际含义:
✓ 大间隔 → 简单的模型 → 更好的泛化
✓ 对噪声和异常值更鲁棒
✓ 减少过拟合的风险
✓ 对新数据的预测更稳定
总结:最佳决策边界的核心特征
-
最大间隔性:距离最近的数据点最远
-
支持向量决定:仅由少数关键样本决定
-
鲁棒性:对小扰动不敏感
-
泛化保证:理论上有更好的泛化性能
-
稀疏性:只需要存储支持向量进行预测
3. 数学基础:从几何到优化
3.1 决策超平面的数学表示
在n维空间中,决策超平面可以表示为:
w₁x₁ + w₂x₂ + ... + wₙxₙ + b = 0或者用向量形式:
wᵀx + b = 0其中:
-
w是法向量(垂直于决策边界) -
b是偏置项 -
x是特征向量
3.2 函数间隔和几何间隔
import numpy as np
class SVMMathBasics:
"""SVM数学基础演示"""
@staticmethod
def functional_margin(w, b, x, y):
"""
函数间隔:衡量分类的确信度
w: 法向量
b: 偏置
x: 数据点
y: 标签(+1 或 -1)
"""
return y * (np.dot(w, x) + b)
@staticmethod
def geometric_margin(w, b, x, y):
"""
几何间隔:点到决策边界的距离
"""
functional = SVMMathBasics.functional_margin(w, b, x, y)
return functional / np.linalg.norm(w)
@staticmethod
def demonstrate_margins():
"""演示函数间隔和几何间隔的区别"""
# 假设的决策边界:x + y - 5 = 0
w = np.array([1, 1]) # 法向量
b = -5
# 数据点
point = np.array([3, 3])
true_label = 1 # 这个点属于正类
func_margin = SVMMathBasics.functional_margin(w, b, point, true_label)
geo_margin = SVMMathBasics.geometric_margin(w, b, point, true_label)
print(f"法向量 w: {w}")
print(f"偏置 b: {b}")
print(f"数据点: {point}")
print(f"函数间隔: {func_margin:.2f}")
print(f"几何间隔: {geo_margin:.2f}")
# 缩放w和b,展示函数间隔的变化但几何间隔不变
w_scaled = 2 * w
b_scaled = 2 * b
func_margin_scaled = SVMMathBasics.functional_margin(w_scaled, b_scaled, point, true_label)
geo_margin_scaled = SVMMathBasics.geometric_margin(w_scaled, b_scaled, point, true_label)
print(f"\n缩放后:")
print(f"函数间隔: {func_margin_scaled:.2f} (发生了变化)")
print(f"几何间隔: {geo_margin_scaled:.2f} (保持不变)")
# 运行演示
SVMMathBasics.demonstrate_margins()运行后得到下列内容:
法向量 w: [1 1]
偏置 b: -5
数据点: [3 3]
函数间隔: 1.00
几何间隔: 0.71
缩放后:
函数间隔: 2.00 (发生了变化)
几何间隔: 0.71 (保持不变)3.3 最大间隔的数学形式化
我们的目标是找到使得最小几何间隔最大的w和b:
max_{w,b} γ
使得:y_i(wᵀx_i + b) ≥ γ, i = 1,...,m
||w|| = 1由于γ = ŷ / ||w||,我们可以重写为:
max_{w,b} ŷ / ||w||
使得:y_i(wᵀx_i + b) ≥ ŷ, i = 1,...,m通过缩放,我们可以设ŷ = 1,问题简化为:
min_{w,b} ½||w||²
使得:y_i(wᵀx_i + b) ≥ 1, i = 1,...,m4. 支持向量的概念
4.1 什么是支持向量?
支持向量是那些位于间隔边界上或违反间隔的数据点:
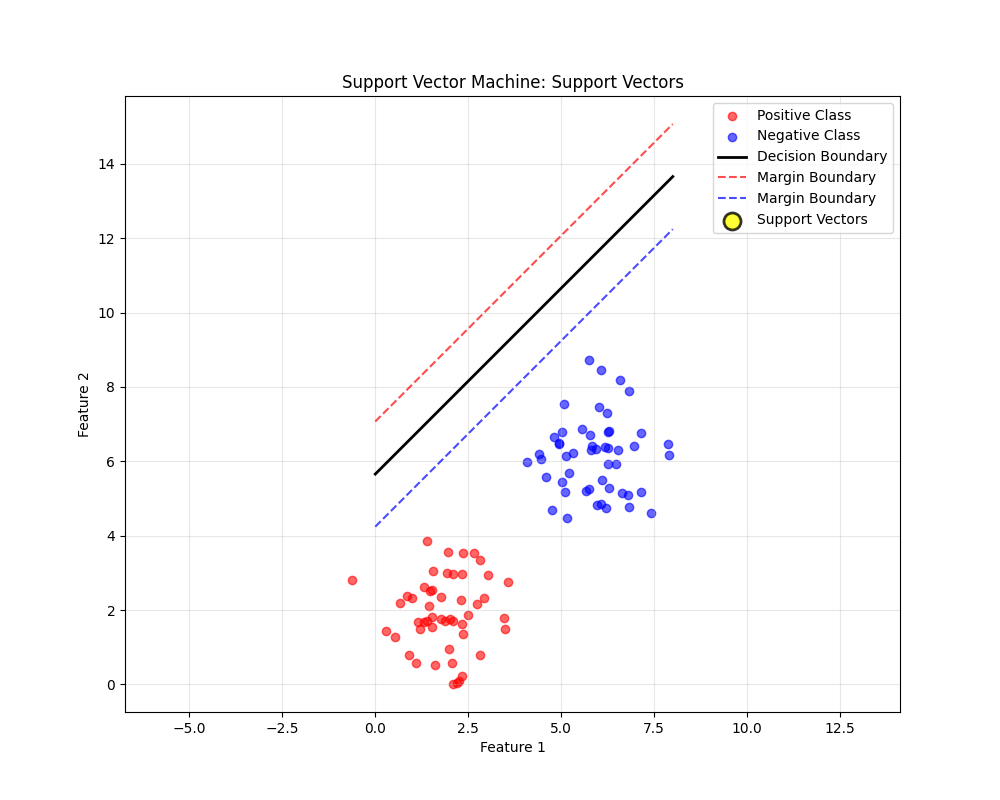
4.2 支持向量的重要性
关键特性:
-
稀疏性:只有支持向量影响最终模型
-
鲁棒性:移除非支持向量不会改变决策边界
-
计算效率:预测时只需要考虑支持向量
5. 硬间隔SVM的数学推导
5.1 优化问题形式化
硬间隔SVM的原始问题:
min_{w,b} ½||w||²
s.t. y_i(wᵀx_i + b) ≥ 1, ∀i5.2 拉格朗日对偶问题
引入拉格朗日乘子α_i ≥ 0,得到拉格朗日函数:
L(w,b,α) = ½||w||² - Σα_i[y_i(wᵀx_i + b) - 1]通过对w和b求导并令导数为0,我们得到:
∂L/∂w = w - Σα_i y_i x_i = 0 ⇒ w = Σα_i y_i x_i
∂L/∂b = -Σα_i y_i = 0 ⇒ Σα_i y_i = 0代入原问题,得到对偶问题:
max_α Σα_i - ½ΣΣα_iα_j y_i y_j x_iᵀx_j
s.t. α_i ≥ 0, ∀i
Σα_i y_i = 05.3 KKT条件
在最优解处,KKT条件必须满足:
-
平稳性:∇wL = 0, ∇bL = 0
-
原始可行性:y_i(wᵀx_i + b) ≥ 1
-
对偶可行性:α_i ≥ 0
-
互补松弛性:α_i[y_i(wᵀx_i + b) - 1] = 0
=== 原始问题 ===
目标函数: min ½||w||²
约束条件: y_i(wᵀx_i + b) ≥ 1, ∀i=== 拉格朗日函数 ===
L(w,b,α) = ½||w||² - Σα_i[y_i(wᵀx_i + b) - 1]
其中 α_i ≥ 0 是拉格朗日乘子=== KKT条件 ===
- 平稳性: ∇wL = 0, ∇bL = 0
- 原始可行性: y_i(wᵀx_i + b) ≥ 1
- 对偶可行性: α_i ≥ 0
- 互补松弛性: α_i[y_i(wᵀx_i + b) - 1] = 0
互补松弛性的含义:
- 如果 α_i > 0,那么 y_i(wᵀx_i + b) = 1 (支持向量)
- 如果 y_i(wᵀx_i + b) > 1,那么 α_i = 0 (非支持向量)
=== 对偶问题 ===
max_α Σα_i - ½ΣΣα_iα_j y_i y_j x_iᵀx_j
约束条件:
α_i ≥ 0, ∀i
Σα_i y_i = 0对偶问题的优势:
-
- 更容易求解(凸二次规划)
-
- 自然地引入核函数
-
- 解具有稀疏性(大部分α_i=0)
-
- 只依赖内积 x_iᵀx_j,便于核技巧
6. 软间隔SVM:处理非线性可分数据
6.1 为什么需要软间隔?
在现实世界中,数据很少是完美线性可分的:
-
噪声:错误标记的样本
-
重叠:类别之间的自然重叠
-
异常值:远离群体的样本
6.2 松弛变量的引入
我们引入松弛变量ξ_i ≥ 0,允许一些样本违反间隔约束:
min_{w,b,ξ} ½||w||² + CΣξ_i
s.t. y_i(wᵀx_i + b) ≥ 1 - ξ_i, ∀i
ξ_i ≥ 0, ∀i其中C是惩罚参数,控制对误分类的容忍度。
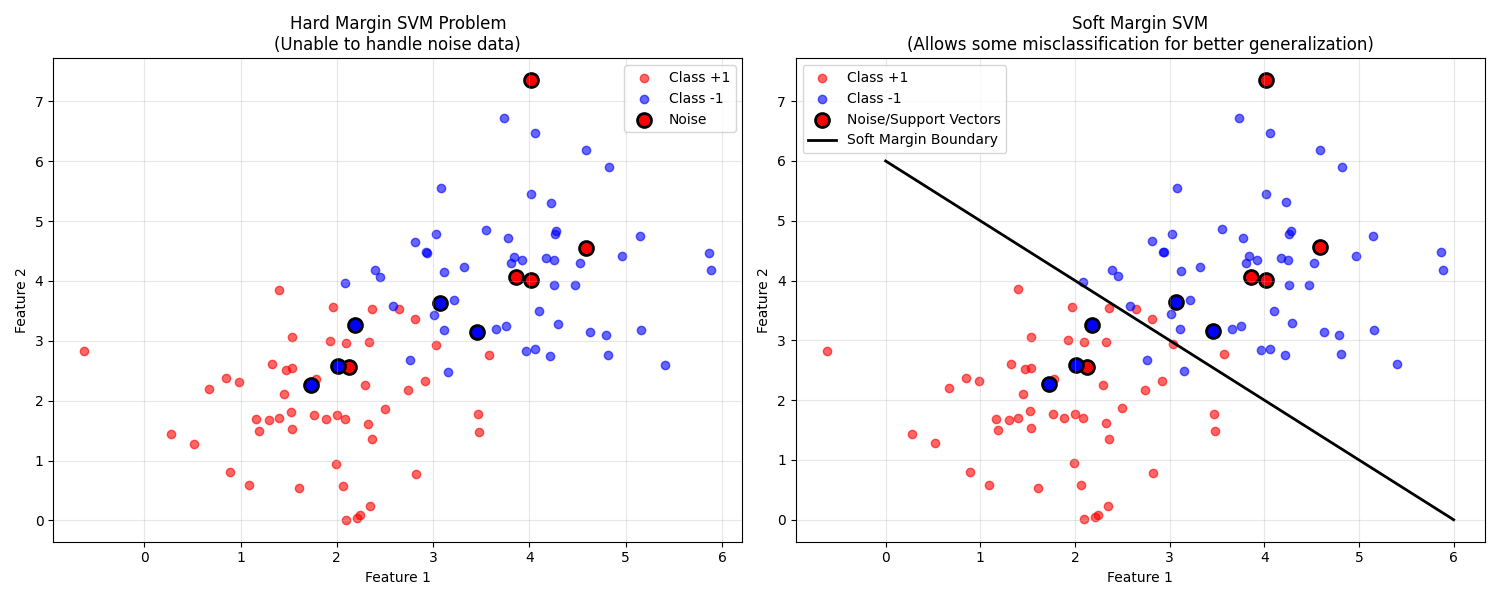
7. 核方法:处理非线性问题
7.1 线性不可分问题
有些数据在原始特征空间中线性不可分,但在更高维空间中可能变得线性可分。
经典例子:异或(XOR)问题
点: (0,0) → 类别0, (1,1) → 类别0, (0,1) → 类别1, (1,0) → 类别1
在二维空间中无法用直线分开7.2 核技巧
我们不需要显式地计算高维特征映射,只需要计算核函数:
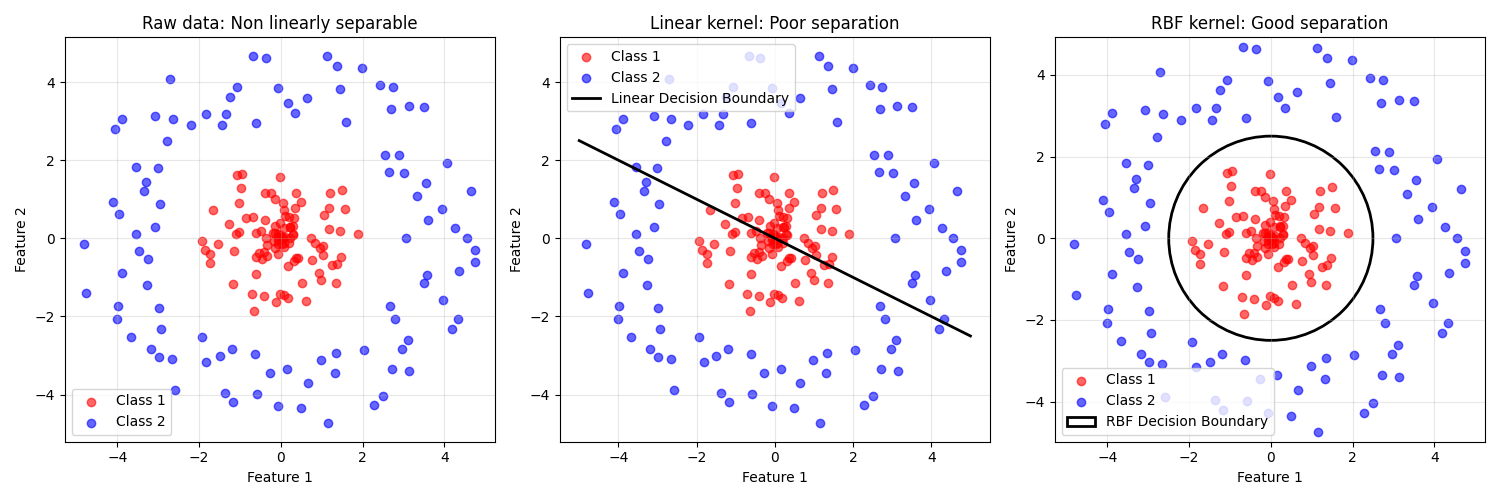
8. SVM实践指南
8.1 如何选择核函数
|----------|-------------|---------|-------|
| 核函数 | 适用场景 | 参数调优 | 计算复杂度 |
| 线性核 | 特征数多,样本数少 | 几乎不需要 | 低 |
| 多项式核 | 数据有一定非线性 | 阶数d,系数c | 中等 |
| RBF核 | 通用选择,强非线性 | 带宽γ | 高 |
| Sigmoid核 | 特定场景,类似神经网络 | 缩放r,偏置c | 中等 |
8.2 参数调优策略
=== SVM参数调优指南 ===
数据形状: (1000, 20)
类别分布: [500 500]
参数搜索网格:
C: [0.1, 1, 10, 100]
gamma: [1, 0.1, 0.01, 0.001]
kernel: ['rbf', 'linear', 'poly']
调优建议:
1. 先用RBF核,它通常效果最好
2. 使用交叉验证避免过拟合
3. 从粗调到精调:先大范围搜索,再小范围细化
4. 考虑使用随机搜索代替网格搜索以节省时间
5. 注意特征缩放:SVM对特征尺度敏感
=== 特征缩放的重要性 ===
SVM基于距离度量,因此对特征尺度敏感
示例特征:
特征1 - 均值: 989.62, 标准差: 90.36
特征2 - 均值: 0.02, 标准差: 0.95
尺度差异: 95.23倍
如果不进行特征缩放:
- 大尺度特征会主导模型
- 小尺度特征的影响被忽略
- 模型性能下降
推荐做法:
- 使用StandardScaler进行标准化
- 或使用MinMaxScaler进行归一化9. SVM的优缺点总结
9.1 优点
-
理论优美:基于坚实的统计学习理论
-
泛化能力强:最大化间隔原理提供良好泛化
-
处理高维数据:在高维空间中表现良好
-
解具有稀疏性:只需要存储支持向量
-
核技巧:可以处理复杂的非线性问题
9.2 缺点
-
计算复杂度:大规模数据训练较慢
-
参数敏感:对核函数和参数选择敏感
-
概率输出:需要额外步骤获得概率估计
-
多分类:需要组合多个二分类器
-
特征缩放:对特征尺度敏感
9.3 适用场景
推荐使用SVM当:
-
数据维度高,样本数中等
-
数据具有复杂的非线性模式
-
需要良好泛化能力的场景
-
问题明确是分类或回归任务
考虑其他方法当:
-
数据量非常大
-
需要概率输出
-
需要模型可解释性
-
处理多分类问题
10. 学习路径建议
10.1 循序渐进的学习步骤
1. 基础理解:
目标:
- 理解最大间隔的直观意义
- 掌握支持向量的概念
- 了解硬间隔和软间隔的区别
实践:
- 在二维数据上可视化SVM决策边界
2. 数学推导:
目标:
- 理解拉格朗日对偶
- 掌握KKT条件
- 了解核技巧的原理
实践:
- 手动推导对偶问题
3. 实践应用:
目标:
- 学会选择核函数
- 掌握参数调优方法
- 理解特征缩放的重要性
实践:
- 在真实数据集上应用SVM
4. 高级主题:
目标:
- 了解SVM的变体(ν-SVM等)
- 学习大规模SVM训练技巧
- 理解与其他算法的关系
实践:
- 实现自定义核函数通过系统性地学习这些内容,你将深入理解支持向量机的核心原理,不仅知道如何使用SVM,还能理解其背后的数学原理和设计思想。这种理解将帮助你在实际应用中更好地选择和使用这个强大的算法。