深入浅出数据结构：手把手实现动态顺序表，从此不再怕数组扩容！

欢迎来到数据结构与算法的世界！今天，我们将深入探讨最基础、最实用的线性数据结构之一------顺序表 (Sequential List) ，并着重讲解其"升级版"------动态顺序表 (Dynamic Array) 的实现细节。

一、顺序表基础介绍
- [1.1 什么是顺序表？](#1.1 什么是顺序表？)
- [1.2 顺序表的基本特性和内存结构](#1.2 顺序表的基本特性和内存结构)
- - [1.2.1 基本特性](#1.2.1 基本特性)
  - [1.2.2 内存结构](#1.2.2 内存结构)
- [1.3 顺序表的应用场景](#1.3 顺序表的应用场景)
[二、静态顺序表 vs 动态顺序表](#二、静态顺序表 vs 动态顺序表)
- [2.1 概念介绍](#2.1 概念介绍)
- [2.2 对比两者的优缺点](#2.2 对比两者的优缺点)
- [2.3 为什么动态顺序表更实用？](#2.3 为什么动态顺序表更实用？)
三、动态顺序表详细实现
- [3.1 顺序表初始化和销毁](#3.1 顺序表初始化和销毁)
- - [3.1.1 操作的功能说明](#3.1.1 操作的功能说明)
  - [3.1.2 完整的源代码展示](#3.1.2 完整的源代码展示)
- [3.2 动态扩容机制](#3.2 动态扩容机制)
- - [3.2.1 操作的功能说明](#3.2.1 操作的功能说明)
  - [3.2.2 完整的源代码展示](#3.2.2 完整的源代码展示)
- [3.3 尾部插入和删除操作](#3.3 尾部插入和删除操作)
- - [3.3.1 操作的功能说明](#3.3.1 操作的功能说明)
  - [3.3.2 完整的源代码展示](#3.3.2 完整的源代码展示)
- [3.4 头部插入和删除操作](#3.4 头部插入和删除操作)
- - [3.4.1 操作的功能说明](#3.4.1 操作的功能说明)
  - [3.4.2 完整的源代码展示](#3.4.2 完整的源代码展示)
- [3.5 任意位置插入和删除操作](#3.5 任意位置插入和删除操作)
- - [3.5.1 操作的功能说明](#3.5.1 操作的功能说明)
  - [3.5.2 完整的源代码展示](#3.5.2 完整的源代码展示)
- [3.6 查找操作](#3.6 查找操作)
- - [3.6.1 操作的功能说明](#3.6.1 操作的功能说明)
  - [3.6.2 完整的源代码展示](#3.6.2 完整的源代码展示)
- [3.7 其他工具函数（判断空、获取大小等）](#3.7 其他工具函数（判断空、获取大小等）)
- - [3.7.1 完整的源代码展示](#3.7.1 完整的源代码展示)
四、完整的测试代码示例
五、顺序表的优缺点总结
- [5.1 优点](#5.1 优点)
- [5.2 缺点](#5.2 缺点)

一、顺序表基础介绍

1.1 什么是顺序表？

你可以将顺序表想象成一个图书馆的书架 或者电影院的排队队伍：

书架（数组）： 书架上的每一本书都有一个固定的位置（下标），这些书是挨个并排、连续存放的。如果你想找第5本书，你可以直接走到那个位置拿到它，非常快。顺序表就像一个使用了数组作为底层结构的书架。
排队队伍（线性结构）： 队伍是"连续的一条直线"，每个人（数据元素）都有一个确定的"前一个"和"后一个"。如果队伍满了，就需要安排一个更大的等待区域（扩容）。

顺序表 就像这样一排物理位置连续 的存储空间，用来存放一系列相同类型的数据元素。数据元素在内存中是顺序存放的，因此得名。

1.2 顺序表的基本特性和内存结构

1.2.1 基本特性

物理存储的连续性： 这是顺序表最核心的特征。所有元素在内存中是紧挨着存放的。
随机访问： 由于存储地址连续，我们可以通过元素的索引（下标）在 O ( 1 ) O(1) O(1) 的时间复杂度内直接访问任何一个元素。
大小可变 (动态)： 动态顺序表通过扩容机制，可以逻辑上存储任意数量的元素。

1.2.2 内存结构

内存地址	元素内容	索引 (Index)
B a s e + 0 × S Base + 0 \times S Base+0×S	元素 0	0
B a s e + 1 × S Base + 1 \times S Base+1×S	元素 1	1
B a s e + 2 × S Base + 2 \times S Base+2×S	元素 2	2
... \dots ...	... \dots ...	... \dots ...
B a s e + i × S Base + i \times S Base+i×S	元素 i i i	i i i

其中 S S S 是每个数据元素的大小。

1.3 顺序表的应用场景

标准库实现： 现代编程语言中的动态数组，如 C++ 的 std::vector 和 Java 的 ArrayList，都是基于动态顺序表实现的。
快速查表： 需要根据索引快速存取数据的场景，例如查找数组中的第 N N N 个数据。
作为底层结构： 许多复杂数据结构（如哈希表、堆）的底层存储都依赖于顺序表的高效随机访问特性。

二、静态顺序表 vs 动态顺序表

顺序表根据其底层存储空间是否可以动态变化，可以分为静态顺序表 和动态顺序表。

2.1 概念介绍

静态顺序表 (Static Array)： 使用固定大小的数组实现。一旦定义，其最大容量就固定了，无法改变。

c 复制代码

// 静态顺序表
// 定义数组的固定长度（容量）
#define N 7      
typedef struct SeqList 
{
	SLDataType a[N]; // 定长数组，用于存储数据 
	int size;      // 记录顺序表中有效数据个数
}SL;

缺点：容量太小会导致溢出，容量太大又会造成空间浪费。

动态顺序表 (Dynamic Array)： 使用动态内存分配 （如 C 语言的 malloc/realloc）来实现。其底层数组的实际容量可以根据存储的元素数量变化而自动调整。

c 复制代码

// 顺序表元素类型（方便修改）
typedef int SLDataType;
// 动态顺序表结构体
typedef struct SeqList
{
	SLDataType* arr; // 指向存储数据的动态数组
	int size;      // 有效元素个数
	int capacity;  // 顺序表容量
}SL;

2.2 对比两者的优缺点

特性	静态顺序表 (Static Array)	动态顺序表 (Dynamic Array)
容量	固定不变	随数据量增大而自动增加
空间效率	容易造成空间浪费或溢出	按需分配，空间利用率高
插入/删除效率	相同，需要移动元素	相同，需要移动元素
实现难度	简单	较复杂，需要实现扩容逻辑
灵活性	差，受限于固定大小	极高，是工程实践的首选

2.3 为什么动态顺序表更实用？

动态顺序表 通过引入动态扩容机制，完美解决了静态顺序表容量固定的致命缺陷：

安全可靠： 它避免了静态数组可能出现的越界访问和溢出问题，让程序能够处理不确定的数据量。
空间优化： 无需预估最大容量，可以从一个很小的初始容量开始，按需增长，提高了内存的利用率。

三、动态顺序表详细实现

本章将基于C语言，详细分析动态顺序表的结构和核心操作的实现。

3.1 顺序表初始化和销毁

3.1.1 操作的功能说明

初始化 (SLInit)：为顺序表变量赋初值，确保指针安全，并将有效元素个数和容量设为 0。
销毁 (SLDestroy)：释放动态申请的内存空间，并将结构体成员重置，防止野指针。

实现思路和算法描述

初始化： 将 arr 设为 NULL，size 和 capacity 设为 0。
销毁： 使用 free(ps->arr) 释放堆上的内存，然后将 ps->arr 重新设为 NULL。

3.1.2 完整的源代码展示

c 复制代码

//顺序表初始化
void SLInit(SL* ps)
{
	assert(ps);
	//避免野指针
	ps->arr = NULL;
	ps->size = 0;
	ps->capacity = 0;
}
//销毁顺序表
void SLDestroy(SL* ps)
{
	assert(ps);
	free(ps->arr);//释放堆上的空间
	ps->arr = NULL;//避免野指针
	ps->size = 0;
	ps->capacity = 0;
}

3.2 动态扩容机制

3.2.1 操作的功能说明

在插入元素前检查当前有效元素个数 (size) 是否等于容量 (capacity)。如果容量不足，则进行内存扩容。

实现思路和算法描述

检查： 判断 ps->capacity == ps->size。
计算新容量： 如果原容量为 0，则设为初始容量 INIT_CAPACITY (4)；否则，将容量翻倍 (2 * ps->capacity)。
重新分配： 使用 realloc 函数尝试重新分配内存。realloc 负责在原地扩展或移动数据到新地址。
- 关键点： 使用临时指针 tmp 接收 realloc 的返回值。如果 realloc 失败，它返回 NULL，但不会释放原有空间；如果直接赋值给 ps->arr，则原空间地址丢失，无法释放，造成内存泄漏。
更新： 如果分配成功 (tmp != NULL)，更新 ps->arr = tmp 和 ps->capacity = new_capacity。

3.2.2 完整的源代码展示

c 复制代码

//检查容量，不允许被外部调用 (static 关键字)
static void SLCheckCapacity(SL* ps)
{
	assert(ps);
	//容量不够
	if (ps->capacity == ps->size)
	{
		//计算新容量：容量为0时初始化为4，否则加倍
		int new_capacity = ps->capacity == 0 ? INIT_CAPACITY : 2 * ps->capacity;
		//申请空间：使用realloc来调整内存大小
		//这里一定不能用arr直接接收，因为还有申请失败的可能
		//如果申请失败，不仅得不到新地址，还会将原来的空间也丢掉
		SLDataType* tmp = (SLDataType*)realloc(ps->arr, new_capacity * sizeof(SLDataType));
		//申请失败，退出
		if (tmp == NULL)
		{
			perror("realloc");
			exit(-1);
		}
		//申请成功后赋值新地址，更新容量
		ps->arr = tmp;
		ps->capacity = new_capacity;
	}
}

3.3 尾部插入和删除操作

3.3.1 操作的功能说明

尾部插入 (SLPushBack)： 在顺序表的末尾添加一个元素。
尾部删除 (SLPopBack)： 删除顺序表末尾的一个元素。

实现思路和算法描述

尾插： 时间复杂度 O ( 1 ) O(1) O(1) (平均)。先调用 SLCheckCapacity 确保容量足够，然后直接将元素放到 ps->arr[ps->size] 位置，最后将 ps->size 增 1。
尾删： 时间复杂度 O ( 1 ) O(1) O(1)。只需要将 ps->size 减 1 即可。在逻辑上，最后一个元素不再属于有效数据，无需真正清空内存。

3.3.2 完整的源代码展示

c 复制代码

//尾插法
void SLPushBack(SL* ps, SLDataType x)
{
	assert(ps);
	SLCheckCapacity(ps); // 检查容量并扩容
	ps->arr[ps->size++] = x;//将x放在顺序表最后一个位置，且有效个数加1
}
//尾删法
void SLPopBack(SL* ps)
{
	//有元素才能删除
	assert(ps && ps->size);
	ps->size--; // 逻辑删除，有效元素个数减一
}

3.4 头部插入和删除操作

3.4.1 操作的功能说明

头部插入 (SLPushFront)： 在顺序表的起始位置 (索引 0) 插入一个元素。
头部删除 (SLPopFront)： 删除顺序表的起始位置 (索引 0) 的元素。

实现思路和算法描述

头插： 时间复杂度 O ( N ) O(N) O(N)。需要将所有现有元素从后往前依次向后移动一位，为新元素腾出位置。
头删： 时间复杂度 O ( N ) O(N) O(N)。需要将索引 1 到 size - 1 的所有元素依次向前移动一位，覆盖掉原来的首元素。

3.4.2 完整的源代码展示

c 复制代码

//头插法
void SLPushFront(SL* ps, SLDataType x)
{
	assert(ps);
	SLCheckCapacity(ps);
	// 将元素从后往前挪，直到索引1位置
	for (int i = ps->size; i > 0; i--)
		ps->arr[i] = ps->arr[i - 1];
	// 插入元素到头部
	ps->arr[0] = x;
	// 元素个数自增
	++ps->size;
}
//头删
void SLPopFront(SL* ps)
{
	assert(ps && ps->size);
	// 将后面的元素往前挪，覆盖掉首元素
	for (int i = 1; i < ps->size; i++)
		ps->arr[i - 1] = ps->arr[i];
	--ps->size;
}

3.5 任意位置插入和删除操作

3.5.1 操作的功能说明

任意位置插入 (SLInsert)： 在指定的 pos (索引) 处插入元素。
任意位置删除 (SLErase)： 删除指定的 pos (索引) 处的元素。

实现思路和算法描述

插入： 时间复杂度 O ( N ) O(N) O(N)。
1. 检查 pos 的合法性：0 <= pos <= ps->size。
2. 检查容量并扩容。
3. 从 ps->size 开始，到 pos + 1 结束，将元素依次向后移动一位。
4. 将新元素放到 ps->arr[pos]。
删除： 时间复杂度 O ( N ) O(N) O(N)。
1. 检查 pos 的合法性：0 <= pos < ps->size。
2. 从 pos 开始，到 ps->size - 1 结束，将后续元素依次向前移动一位，覆盖掉待删除元素。
3. ps->size 减 1。

3.5.2 完整的源代码展示

c 复制代码

//在指定位置插入元素
void SLInsert(SL* ps, int pos, SLDataType x)
{
	assert(ps);
	//判断插入位置是否合法：pos可以等于size，表示尾插
	assert(pos >= 0 && pos <= ps->size);
	//检查容量
	SLCheckCapacity(ps);
	//将pos之后的元素后移
	for (int i = ps->size; i > pos; i--)
		ps->arr[i] = ps->arr[i - 1];
	ps->arr[pos] = x;
	++ps->size;
}
//在指定位置删除元素
void SLErase(SL* ps, int pos)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);
	//将pos之后的元素往前挪
	for (int i = pos; i < ps->size; i++)
		ps->arr[i] = ps->arr[i + 1];
	--ps->size;
}

3.6 查找操作

3.6.1 操作的功能说明

按值查找 (SLFind)： 在顺序表中查找值为 x 的元素，并返回其第一次出现的索引。

实现思路和算法描述

查找： 时间复杂度 O ( N ) O(N) O(N)。
1. 从索引 0 开始遍历到 ps->size - 1。
2. 如果当前元素等于目标值 x，立即返回当前索引。
3. 如果遍历结束仍未找到，返回 -1 表示查找失败。

3.6.2 完整的源代码展示

c 复制代码

//按值查找
int SLFind(SL* ps, SLDataType x)
{
	assert(ps);
	//从头开始遍历查找
	for (int i = 0; i < ps->size; i++)
		if (ps->arr[i] == x)
			return i;//找到返回下标
	return -1;//没找到
}

3.7 其他工具函数（判断空、获取大小等）

函数名	功能说明	实现思路
`SLGetLength`	获取顺序表有效元素的个数 (长度)	返回 `ps->size`。
`SLIsEmpty`	判断顺序表是否为空	判断 `ps->size == 0`。
`SLIsFull`	判断顺序表是否已满	判断 `ps->size == ps->capacity`。
`SLClear`	清空顺序表	将 `ps->size` 置为 0 (逻辑清空，不释放内存)。
`SLPrint`	打印顺序表	遍历 `ps->arr` 从 0 到 `ps->size - 1` 并打印。
`SLReverse`	原地反转顺序表	使用双指针 `left` 和 `right`，从两端向中间交换元素。

3.7.1 完整的源代码展示

c 复制代码

//清空顺序表
void SLClear(SL* ps)
{
	assert(ps);
	//只把元素有效个数置为0，空间留下，后续继续使用
	ps->size = 0;
}
//获取顺序表长度
int SLGetLength(SL* ps)
{
	assert(ps);
	return ps->size;
}
//判断表空
bool SLIsEmpty(SL* ps)
{
	assert(ps);
	return ps->size == 0;
}
//顺序表反转
void SLReverse(SL* ps)
{
	assert(ps);
	int left = 0, right = ps->size - 1;
	while (left < right)
	{
		// 交换元素
		SLDataType tmp = ps->arr[left];
		ps->arr[left] = ps->arr[right];
		ps->arr[right] = tmp;
		++left; 
		--right;
	}
}
//打印顺序表
void SLPrint(SL* ps)
{
	assert(ps);
	for (int i = 0; i < ps->size; i++)
	{
		printf("%d ", ps->arr[i]);
	}
	puts(" ");
}

四、完整的测试代码示例

为了演示上述动态顺序表的功能，这里提供一个完整的测试函数。

c 复制代码

// 测试顺序表的基础操作
void TestSeqList1()
{
	SL sl;
	SLInit(&sl); // 初始化
	printf("--- 1. 尾插操作 ---\n");
	SLPushBack(&sl, 10);
	SLPushBack(&sl, 20);
	SLPushBack(&sl, 30);
	SLPushBack(&sl, 40); // 此时触发第一次扩容
	SLPrint(&sl); // 输出: 10 20 30 40 
	printf("Length: %d, Capacity: %d\n", SLGetLength(&sl), sl.capacity); // 4, 4/8
	SLPushBack(&sl, 50); // 触发扩容
	SLPushBack(&sl, 60);
	SLPrint(&sl); // 输出: 10 20 30 40 50 60 
	printf("Length: %d, Capacity: %d\n", SLGetLength(&sl), sl.capacity); // 6, 8
	printf("--- 2. 头插操作 ---\n");
	SLPushFront(&sl, 5);
	SLPushFront(&sl, 1);
	SLPrint(&sl); // 输出: 1 5 10 20 30 40 50 60
	printf("Length: %d, Capacity: %d\n", SLGetLength(&sl), sl.capacity); // 8, 8 (如果初始容量是4，此时会再次扩容到16)
	printf("--- 3. 任意位置插入 (pos=2, 888) ---\n");
	SLInsert(&sl, 2, 888);
	SLPrint(&sl); // 输出: 1 5 888 10 20 30 40 50 60 
	printf("--- 4. 按值查找 (Find 30) ---\n");
	int pos = SLFind(&sl, 30);
	if (pos != -1)
		printf("Element 30 found at index: %d\n", pos); // 5
	printf("--- 5. 尾删和头删 ---\n");
	SLPopBack(&sl); // 删 60
	SLPopFront(&sl); // 删 1
	SLPrint(&sl); // 输出: 5 888 10 20 30 40 50 
	printf("--- 6. 任意位置删除 (pos=1, 删 888) ---\n");
	SLErase(&sl, 1);
	SLPrint(&sl); // 输出: 5 10 20 30 40 50 
	printf("--- 7. 顺序表反转 ---\n");
	SLReverse(&sl);
	SLPrint(&sl); // 输出: 50 40 30 20 10 5 
	printf("--- 8. 清空和销毁 ---\n");
	SLClear(&sl);
	printf("Is Empty: %s\n", SLIsEmpty(&sl) ? "True" : "False");
	SLDestroy(&sl); // 释放内存
}

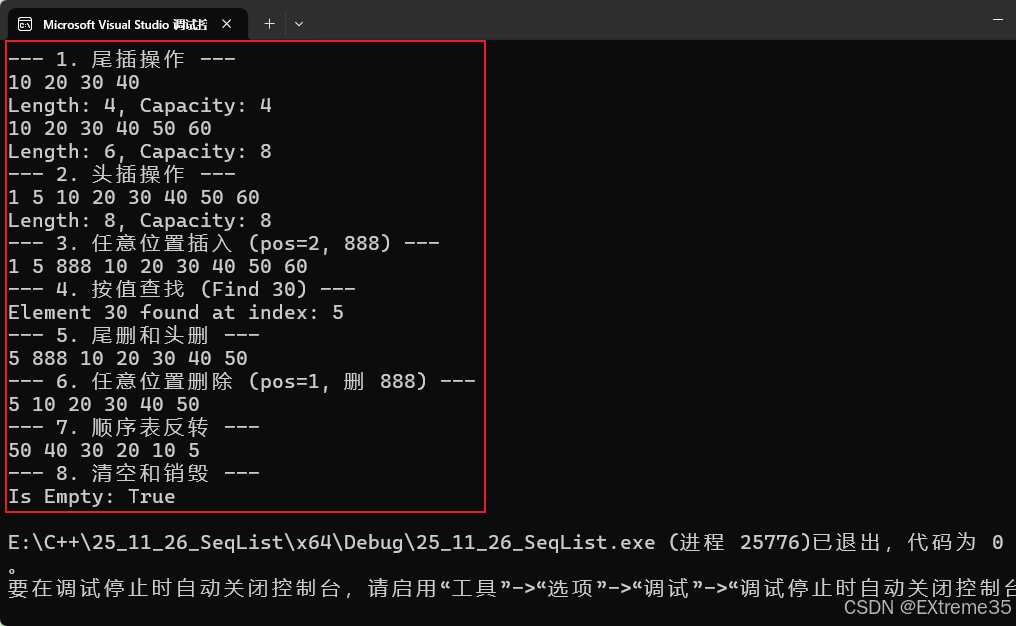
顺序表 8 项操作全程绿灯：尾插头插、任意位置删插、按值查找、反转、清空均符合预期，容量两倍扩容正常，无越界无泄漏，进程正常退出------接口正确，内存安全。

五、顺序表的优缺点总结

5.1 优点

随机访问高效： 基于物理连续的内存地址，可以通过索引 O ( 1 ) O(1) O(1) 的时间复杂度访问任何元素。
缓存友好： 元素存储在一起，CPU 可以高效地利用缓存，从而提高数据读取速度。
尾部操作高效： 尾部插入和删除操作不需要移动元素，平均时间复杂度为 O ( 1 ) O(1) O(1) (只有扩容时为 O ( N ) O(N) O(N))。
空间利用率高 (动态)： 动态特性使得它能按需分配空间，不会有太大的闲置浪费。

5.2 缺点

插入/删除效率低： 在头部或中间位置进行插入或删除操作时，需要移动 N / 2 N/2 N/2 (平均) 个元素，时间复杂度为 O ( N ) O(N) O(N)。
扩容成本高： 当容量不足需要扩容时，需要重新申请更大的内存空间，并将所有旧数据拷贝到新空间，这是一个 O ( N ) O(N) O(N) 的操作。
空间限制： 虽然是动态的，但由于需要连续的内存空间，当需要存储海量数据时，可能难以找到一块足够大的连续内存区域。

深入浅出数据结构：手把手实现动态顺序表，从此不再怕数组扩容！

目录

一、顺序表基础介绍

1.1 什么是顺序表？

1.2 顺序表的基本特性和内存结构

1.2.1 基本特性

1.2.2 内存结构

1.3 顺序表的应用场景

二、静态顺序表 vs 动态顺序表

2.1 概念介绍

2.2 对比两者的优缺点

2.3 为什么动态顺序表更实用？

三、动态顺序表详细实现

3.1 顺序表初始化和销毁

3.1.1 操作的功能说明

3.1.2 完整的源代码展示

3.2 动态扩容机制

3.2.1 操作的功能说明

3.2.2 完整的源代码展示

3.3 尾部插入和删除操作

3.3.1 操作的功能说明

3.3.2 完整的源代码展示

3.4 头部插入和删除操作

3.4.1 操作的功能说明

3.4.2 完整的源代码展示

3.5 任意位置插入和删除操作

3.5.1 操作的功能说明

3.5.2 完整的源代码展示

3.6 查找操作

3.6.1 操作的功能说明

3.6.2 完整的源代码展示

3.7 其他工具函数（判断空、获取大小等）

3.7.1 完整的源代码展示

四、完整的测试代码示例

五、顺序表的优缺点总结

5.1 优点

5.2 缺点