问题引入:
给定一个数组和一个目标值 k,求有多少个子数组的和等于 k?
比如数组 [1, 1, 1],k = 2,答案是 2, 有两个子数组 [1,1] 的和为 2。
最直观的想法: 暴力求解
python
def subarraySum_bruteforce(nums, k):
count = 0
n = len(nums)
# 枚举所有子数组
for i in range(n):
for j in range(i, n):
# 计算 nums[i:j+1] 的和
subarray_sum = sum(nums[i:j+1])
if subarray_sum == k:
count += 1
return count这个方法的问题很明显:O(n³) 的时间复杂度。当数组有 10, 000 个元素时,提交后 LC 应该就会报超时了。
优化一下
不再每次都调用 sum(nums[i:j+1])(O(n) 的操作),而是用一个变量 current_sum 逐步累加。
python
def subarraySum_better(nums, k):
count = 0
n = len(nums)
for i in range(n):
current_sum = 0
for j in range(i, n):
current_sum += nums[j] # 累加,避免重复计算
if current_sum == k:
count += 1
return count好一点了,现在是 O(n²)。但对于大数据集,这仍然不够快。
基于前缀和的优化思路
还能不能再进行优化下, 让这个问题可以在 O(n) 时间内解决,仍然有很严重的重复计算的问题
如:
python
for i in range(n):
current_sum = 0
for j in range(i, n):
current_sum += nums[j] # 这一行做了大量重复计算!看看一个例子,数组是 [1, 2, 3]:
i=0 时:
j=0: 1
j=1: 1 + 2 ← 1 又加了一遍
j=2: 1 + 2 + 3 ← 1 和 2 又加了一遍
i=1 时:
j=1: 2
j=2: 2 + 3 ← 2 又加了一遍在这个过程中,1 被加了 2 次,2 被加了 2 次,3 被加了 1 次。 同一个数字一直在被重复加! 所以我们发现了可以优化的问题和空间: 在计算过程中存在重复的加法计算。明明 1 + 2 已经算过了,结果到了 j=2 又要再加一遍 1 和 2。
能不能把计算过的结果缓存下来, 下次使用时直接从缓存读取, 避免重复呢?
这里就引入了经典的技巧:
前缀和, 如果我们能提前把所有的"前缀和"计算并缓存起来 ,就不用每次都重新累加了!这就是前缀和 的核心思想:与其每次都从头开始累加,不如一开始就把"从开头到每个位置的累加和"全部缓存下来。这样,计算任意子数组的和就变成了一个简单的减法,完全避免了重复累加!
什么是前缀和?
前缀和就是"从数组开头到当前位置的累加和"。
数组: [1, 2, 3, 4, 5]
前缀和: [0, 1, 3, 6, 10, 15]
↑ ↑ ↑ ↑ ↑ ↑
起点 1 1+2 1+2+3 ...
prefix[i] = nums[0] + nums[1] + ... + nums[i]前缀和:快速计算子数组和
通过前缀和,计算任意子数组的和就变成了一次减法:
子数组 nums[i:j+1] 的和 = prefix[j] - prefix[i-1]
prefix[j]= nums[0] + nums[1] + ... + nums[j]prefix[i-1]= nums[0] + nums[1] + ... + nums[i-1]- 两者一减,中间的元素就都消掉了,剩下 nums[i] + nums[i+1] + ... + nums[j]
一个简单例子:
数组: [1, 2, 3, 4, 5]
索引: 0 1 2 3 4
前缀和:
prefix[0] = 1
prefix[1] = 1 + 2 = 3
prefix[2] = 1 + 2 + 3 = 6
prefix[3] = 1 + 2 + 3 + 4 = 10
prefix[4] = 1 + 2 + 3 + 4 + 5 = 15现在要计算 nums[1:4](即索引 1, 2, 3 的元素:2, 3, 4)的和:
直接用公式:prefix[3] - prefix[0] = 10 - 1 = 9 使用前缀和缓存了之前计算的结果: 用一次减法秒算,不用重复累加。
回来看下原问题:有多少个子数组的和等于 k? 遍历数组,当前位置是 i,前 i 个数字的和是 x。 我们想找:有多少个之前的位置 j,使得从 j+1 到 i 的子数组和等于 k?
用前缀和的思路则求解过程编程:
prefix[i] - prefix[j] = k
=> prefix[j] = prefix[i] - k
=> prefix[j] = x - k所以问题转换成了:在 i 之前,有多少个位置的前缀和等于 (x - k)?
如何存储前缀和? 哈希表!
哈希表的作用
用一个哈希表来记录:
- 键:前缀和的值
- 值:这个前缀和出现过多少次
python
def subarraySum_optimal(nums, k):
# 哈希表:记录前缀和出现的次数
prefix_count = {0: 1} # 初始化:前缀和为0出现1次
current_sum = 0
result = 0
for num in nums:
current_sum += num
# 关键问题:之前有多少个前缀和等于 (current_sum - k)?
target = current_sum - k
if target in prefix_count:
result += prefix_count[target]
# 更新哈希表:记录当前前缀和
prefix_count[current_sum] = prefix_count.get(current_sum, 0) + 1
return result优化思路总结
| 阶段 | 做法 | 时间 | 问题 |
|---|---|---|---|
| O(n³) | 每次都 sum(nums[i:j+1]) |
太慢 | 大量重复累加 |
| O(n²) | 用变量逐步累加 | 还是慢 | 仍然要对每个 (i,j) 对检查一遍 |
| O(n) | 前缀和 + 哈希表 | 快 | 反向查询,一遍扫描搞定 |
优化思路: 只扫描一遍数组,每个元素处理一次,哈希表的查询和插入都是 O(1)。
前缀和的进阶用法, 一个表格搞定
| 题目类型 | 关键变化 | 解法思路 |
|---|---|---|
| 和为 k 的子数组个数 | 求个数 | 哈希表记录前缀和出现次数 |
| 最长和为 k 的子数组 | 求长度 | 哈希表记录前缀和第一次出现的位置 |
| 最长 0 和 1 相等的子数组 | 把 0 看作 -1 | 问题转化为"和为 0 的子数组" |
| 子数组和模 m 余 r | 模运算 | 哈希表记录 prefix_sum % m |
例子1:最长和为 k 的子数组
python
def maxSubarrayLen(nums, k):
prefix_sum = 0
first_occurrence = {0: -1} # 前缀和为0首次出现在位置-1
max_len = 0
for i, num in enumerate(nums):
prefix_sum += num
target = prefix_sum - k
if target in first_occurrence:
# 找到了一个和为k的子数组
max_len = max(max_len, i - first_occurrence[target])
# 只记录第一次出现(为了最大化长度)
if prefix_sum not in first_occurrence:
first_occurrence[prefix_sum] = i
return max_len例子2: 最大 XOR 子数组
类似的思路应用还有最大 XOR 子数组
原理是一样的,但实现不同
前缀XOR: prefix_xor[i] = arr[0] ^ arr[1] ^ ... ^ arr[i]
子数组 [j+1, i] 的XOR值 = prefix_xor[i] ^ prefix_xor[j]问题: 给定数组,求最大的子数组 XOR 值。
暴力想法: 枚举所有子数组,计算 XOR,O(n²)。
优化想法: 对每个 i,找到最优的 j 使得 prefix_xor[i] ^ prefix_xor[j] 最大。
这里不再用哈希表, 因为我们要最大化,不是查询具体值,引入新的数据结果 Trie 树按二进制位贪心匹配:
Trie树定义很简单:
python
class TrieNode:
def __init__(self):
self.children = {}
def findMaximumXOR(nums):
root = TrieNode()
max_xor = 0
prefix_xor = 0
for num in nums:
prefix_xor ^= num
# 将前缀XOR的二进制表示插入Trie
node = root
for i in range(31, -1, -1):
bit = (prefix_xor >> i) & 1
if bit not in node.children:
node.children[bit] = TrieNode()
node = node.children[bit]
# 贪心地找最大XOR:尽量走不同的分支
node = root
current_xor = 0
for i in range(31, -1, -1):
bit = (prefix_xor >> i) & 1
# 优先选择相反的bit
opposite_bit = 1 - bit
if opposite_bit in node.children:
current_xor |= (1 << i)
node = node.children[opposite_bit]
else:
node = node.children[bit]
max_xor = max(max_xor, current_xor)
return max_xor这个方法虽然看起来复杂,但思想是一致的:用数据结构快速查询之前的信息,避免暴力枚举。
总结:类似问题的解题套路
题目共性:
- 题目问"子数组"满足某个条件
- 条件涉及"和"、"XOR"、"乘积"等可以累加的操作
- 暴力解法是 O(n²) 或更差
整体的解题流程:
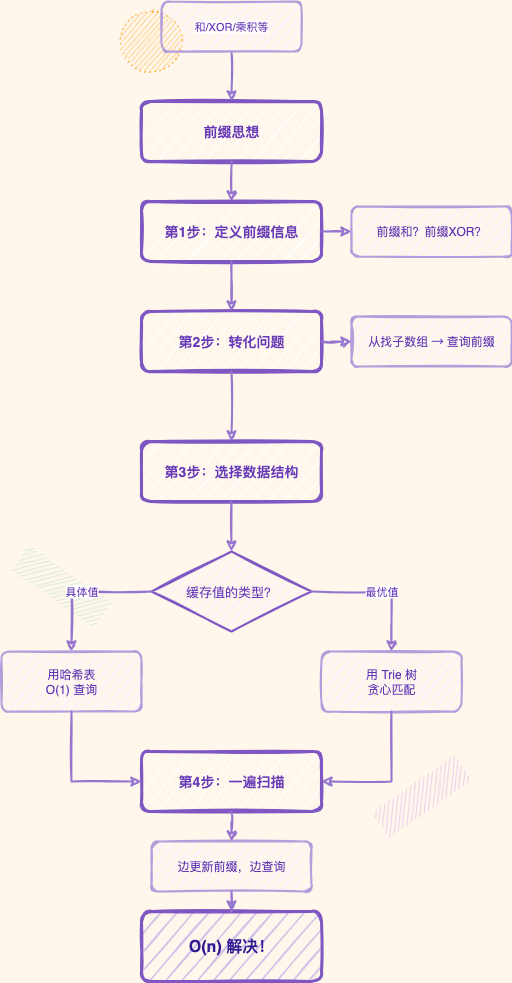
- 定义前缀信息(前缀和、前缀XOR等)
- 转化问题:从"找子数组"转化为"查询之前的前缀信息"
- 选择数据结构 :
- 需要查询具体值?用哈希表
- 需要查询最优值?用Trie树
- 一遍扫描:从左到右扫描数组,边更新边查询
最后
这个技巧整体还是比较好用的, 通过理解"前缀和 + 哈希表"的思路与技巧,其实很多看似不同的题目其实都是同一个套路的变种, 找到重复计算的地方, 用缓存消除重复计算。
这样就有可能能从 O(n²) 的暴力简单思维中找到优化点,写出一个 O(n) 的优雅解法。