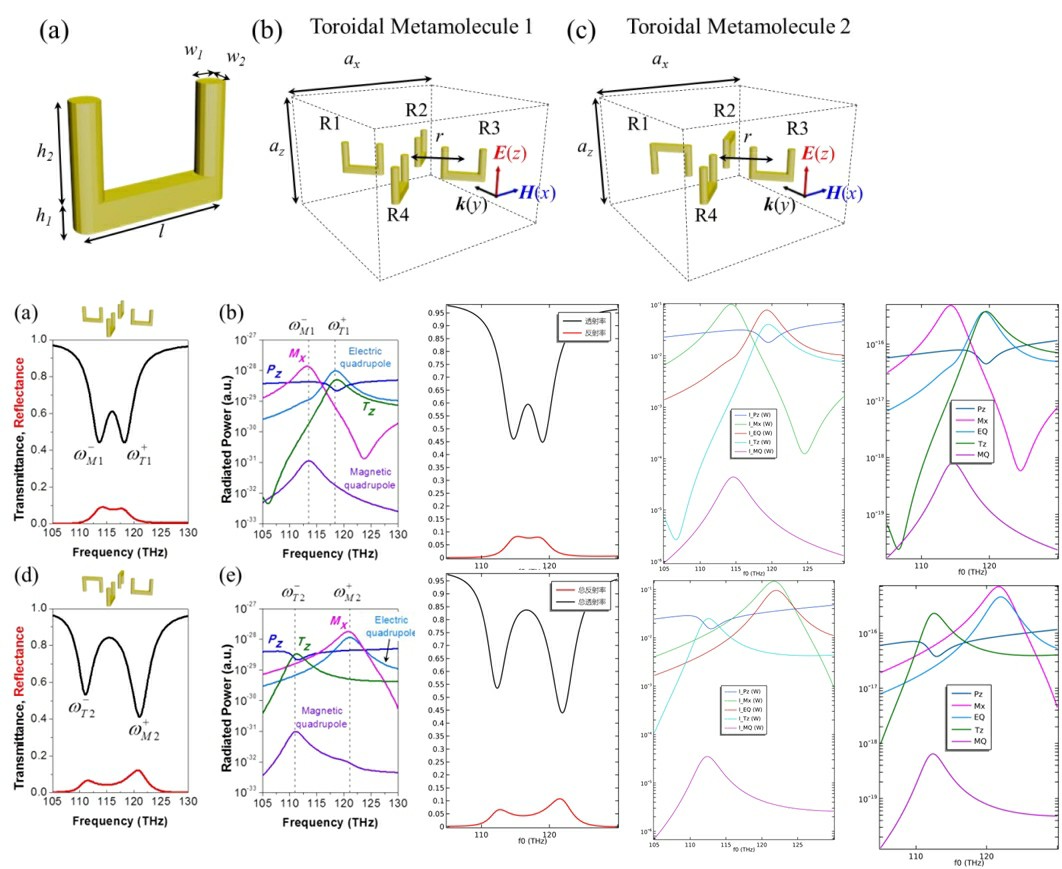
Comsol仿真金属纳米颗粒超表面的多极分解之旅

comsol仿真金属纳米颗粒超表面的多极分解，采用电流，极化率两种方式进行分解-comsol模型，

在研究金属纳米颗粒超表面的特性时，多极分解是一个非常有用的工具。今天咱们就来唠唠如何用Comsol对金属纳米颗粒超表面进行多极分解，而且还是通过电流和极化率这两种有趣的方式哦。

Comsol模型搭建基础

首先得搭建起Comsol模型。在Comsol里，我们要构建金属纳米颗粒超表面的几何结构。比如说，我们设定纳米颗粒是球形的（当然实际研究中形状可能多样），可以通过Comsol的几何建模工具轻松创建。

python 复制代码

# 这里虽然Comsol不是用Python建模，但类似思路，假设创建一个半径为r的球体
r = 10e - 9  # 半径10纳米
# 想象在Comsol里类似通过参数化设定球体半径

这段"伪代码"想表达的就是在建模时，参数化设定对模型灵活性的重要性，在Comsol中通过设定合适的参数，能轻松调整纳米颗粒的大小、形状等关键属性。

基于电流的多极分解

基于电流的多极分解，核心在于理解纳米颗粒表面电流分布与多极子的关系。在Comsol中，我们通过求解麦克斯韦方程组来得到电流分布。

matlab 复制代码

% 假设我们用类似Matlab代码思路来理解
% 麦克斯韦方程组中的安培定律简化形式
curl(H) = J + dD/dt
% 在Comsol里就是通过求解这个方程来获得电流密度J

这里的电流密度J经过一系列数学处理后，可以分解为不同阶数的多极子电流。比如电偶极子电流、磁偶极子电流等。通过分析这些电流分布，我们能深入了解纳米颗粒与电磁场相互作用时，不同多极子的贡献。例如，电偶极子电流在特定频率下可能主导了纳米颗粒的散射特性，通过Comsol的后处理功能，我们可以直观地看到电偶极子电流在纳米颗粒表面的分布情况，就像这样：

python 复制代码

# 假设用Python来可视化电流分布（实际Comsol有自己后处理方式）
import matplotlib.pyplot as plt
import numpy as np

# 模拟的电流分布数据
current_distribution = np.random.rand(100) 
plt.plot(current_distribution)
plt.title('Current Distribution on Nanoparticle Surface')
plt.xlabel('Position on Surface')
plt.ylabel('Current Density')
plt.show()

这能帮助我们定性地理解电流多极分解的结果。

基于极化率的多极分解

极化率的多极分解又是另一番天地。极化率描述了纳米颗粒在电场作用下产生极化的难易程度。在Comsol中，我们同样求解相关的电场方程来获得极化强度。

matlab 复制代码

% 极化强度P与电场E关系简化形式
P = chi * E
% chi就是极化率，通过Comsol求解电场E后可得到P

得到极化强度后，我们同样可以将其分解为不同阶数的多极子极化。与电流多极分解类似，不同阶数的极化多极子对纳米颗粒超表面的光学性质有着不同的影响。比如说，高阶的电四极子极化可能在特定的光频率下对超表面的吸收特性有着关键作用。我们在Comsol中通过查看极化强度的分布云图，能直观看到不同区域极化的强弱，进而分析多极子极化的贡献。

通过这两种多极分解方式，我们在Comsol里对金属纳米颗粒超表面有了更深入的理解，为进一步研究超表面的光学、电磁学等特性打下了坚实基础。在实际科研中，灵活运用这两种多极分解方式，能挖掘出超表面更多有趣且实用的物理性质。