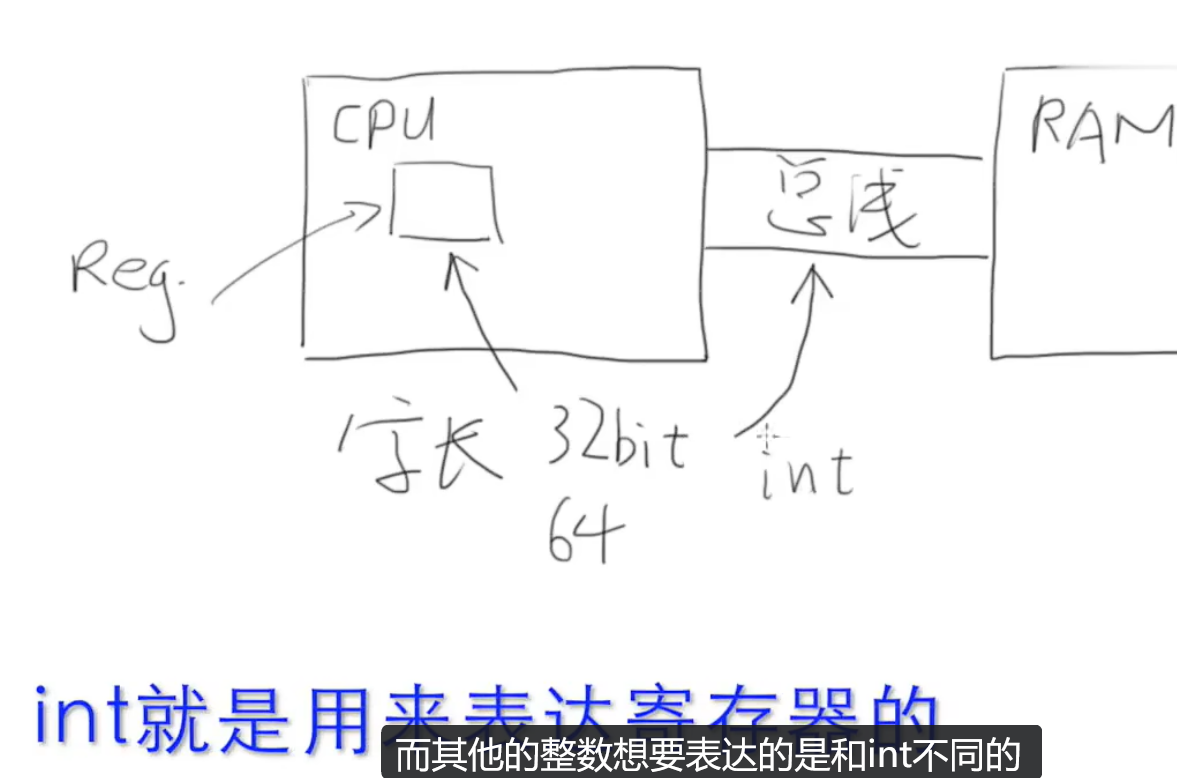
计算机只会做加法 ，不会做减法。比如要算 0-1（其实就是 -1），或者算 -1+1=0，计算机得把 "减法" 变成 "加法" 来算 ------补码就是干这个的：把负数转换成一个 "正数"，让它和原数相加后，结果刚好是 "满位溢出"，溢出后剩下的就是 0。
第一步：先看正数的 8 位二进制
例子里的数都是 8 位（比如 0 是00000000，1 是00000001）：
- 0 的 8 位二进制：
00000000 - 1 的 8 位二进制：
00000001
第二步：解决 "-1+1=0" 的问题
我们希望计算机算 -1 + 1 能得到 0，但计算机只会加，那 -1 得变成啥数，和00000001相加后能等于 0？
看例子里的算式：11111111 + 00000001 = 100000000
注意：8 位二进制只能存 8 个数 ，所以100000000里的第 9 位（最前面的 1）会被 "丢掉"，剩下的后 8 位就是00000000（也就是 0）。
刚好！11111111 + 00000001 溢出后等于 0，所以我们就把 11111111 规定为 -1 的补码。
第三步：验证 "0-1=-1"
例子里说 "因为 0-1→-1，所以 - 1=00000000 - 00000001"。
但二进制里00000000减00000001不够减，得借位 （相当于借一个 "8 位满值"）：00000000 借位后变成 100000000（相当于十进制的 256），然后减00000001：100000000 - 00000001 = 11111111
所以 -1 的补码就是 11111111（和第二步的结果一致）。
第四步：补码的通用规则
对于 8 位二进制（n=8），一个负数-a的补码 = 2^8 - a（因为 2^8=256，是 8 位二进制能存的 "满值"）：
- 比如
-1的补码 = 256-1=255，255 的 8 位二进制就是11111111； - 再比如
-2的补码 = 256-2=254，对应的 8 位二进制是11111110
二进制串本身没有 "固定身份"------ 它既不是天生的 "补码"，也不是天生的 "十进制"。就像一串字符 "12"，可以是数字 "十二"，也可以是月份 "十二月"，全看我们用什么规则去理解
同一串二进制，规则不同，解读出的数字就不同
这里的 8 位二进制是按 ** 补码（有符号数）** 解读的 ------ 补码规则是：
- 第 1 位（最高位）是符号位 ：
0表示正数 / 0，1表示负数； - 剩下的 7 位是数值位，用来表示具体大小。
第二步：拆分 8 位二进制的 3 类情况
一个字节有 8 位，所有可能的二进制组合是 00000000 ~ 11111111（共 256 种），这些组合对应 3 类数值：
1. 单独的 0：00000000 → 对应十进制0
最高位是 0（符号位为正），数值位全是 0，所以直接是 0。
2. 正数范围：00000001 ~ 01111111 → 对应十进制1 ~ 127
- 符号位是 0（表示正数），剩下 7 位是数值位；
- 数值位最小是
0000001（对应 1），最大是1111111（计算：\(2^6+2^5+...+2^0=64+32+16+8+4+2+1=127\)）； - 所以正数能表示
1~127。
3. 负数范围：10000000 ~ 11111111 → 对应十进制-128 ~ -1
- 符号位是 1（表示负数），剩下 7 位是补码的 "数值部分"；
- 补码负数转十进制的规则是：\(- (2^8 - 二进制对应的无符号数)\)（2^8 是 8 位的 "满值"=256）。
举两个关键例子：
- 最大的负数（最接近 0）：
11111111→ 无符号数是 255 → \(- (256-255) = -1\)； - 最小的负数：
10000000→ 无符号数是 128 → \(- (256-128) = -128\)；
所以负数能表示-128 ~ -1。
第三步：总结
1 个字节（8 位补码）能表示的所有数值是：-128 ~ 0 ~ 127（共 256 个数，刚好对应00000000 ~ 11111111的 256 种二进制组合）
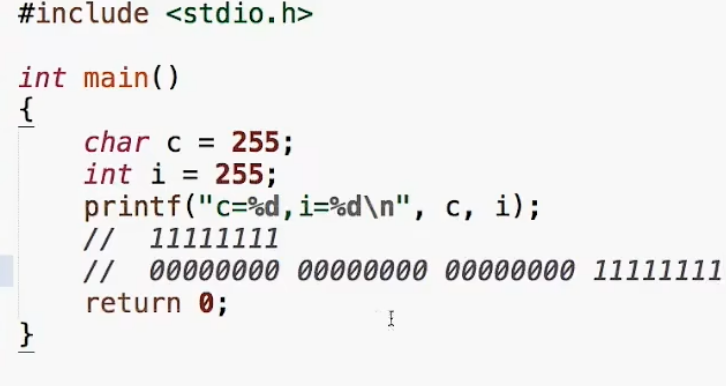
char类型 ：在绝大多数电脑里，char只占 1 个字节（8 位二进制），就像一个 "小盒子"，最多只能装 8 个 0 或 1；int类型 ：通常占 4 个字节（32 位二进制），是一个 "大盒子"，能装 32 个 0 或 1。
255 转换成二进制是 11111111（8 个 1），刚好填满 1 个字节。
对于 char c = 255;：
char 是 "1 字节的有符号类型"------ 它的规则是：
- 只用 8 位存数据；
- 最高位（第 1 位）是 "符号位"：
0表示正数，1表示负数； - 超出范围（
char能表示的范围是-128 ~ 127）会 "溢出"，按补码规则解读。
255 的 8 位二进制是 11111111：
- 最高位是 1（符号位为负）；
- 按补码规则（之前讲过的），
11111111表示-1（因为11111111作为 8 位补码，对应十进制 - 1）； - 所以
c输出-1。
对于 int i = 255;：
int 是 "4 字节的有符号类型"------ 它的规则是：
- 用 32 位存数据，255 的 32 位二进制是
00000000 00000000 00000000 11111111（前面补 24 个 0，凑满 32 位）； - 最高位是 0（符号位为正），所以直接按正数解读，就是 255；
- 所以
i输出255。
运行这段代码，会打印：c=-1, i=255
同样的数值 255，因为存在不同大小的 "盒子"（char和int）里，且 "解读规则" 不同：
- 小盒子（
char）装不下 255，按补码规则变成了 - 1； - 大盒子（
int）装得下，直接按正数解读为 255
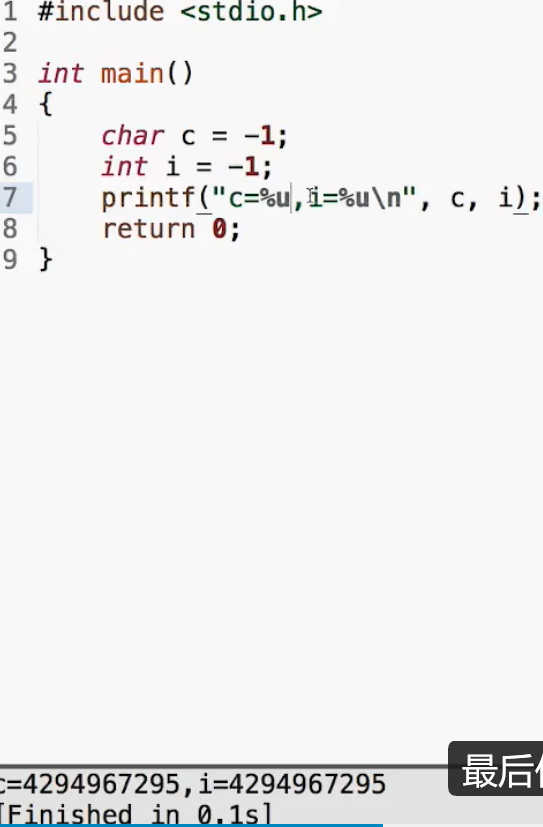
unsigned 是 C 里的一个 "规则开关"------ 它的作用是告诉计算机："这个变量里的二进制，没有正负，全是正数"。
举个之前的例子：
- 普通
char（默认 "有符号"）：8 位二进制11111111会被解读成-1（因为最高位是符号位）； - 加
unsigned变成unsigned char：同样的11111111会被解读成255（因为没有符号位，全是数值位）。
二、图里的 "字面量加 u/U" 是啥意思？
"字面量" 就是你直接写的数字（比如 255），加 u 或 U（比如 255U）是告诉计算机："这个数字是无符号的，别把它当成负数"。
比如写 unsigned int a = 255U; ------ 这里的 255U 明确说 "我是无符号数"，和 unsigned int 的规则对应上。
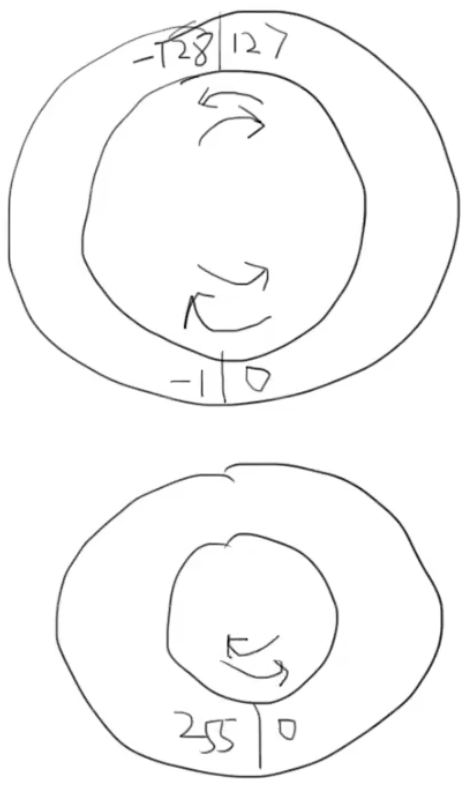
三、那两个 "圈图" 是啥意思？
这两个圈是 **"二进制存满了会'绕圈'"** 的示意图（因为变量的存储空间是固定的，存不下就会溢出）：
第一个圈：有符号数（不带 unsigned，比如普通 char）
- 范围是
-128 ~ 127（8 位有符号数的范围）； - 圈是 "循环的"：比如
127再加 1，存不下了，就会 "绕到"-128；-128再减 1，会 "绕到"127。 - 图里的箭头就是这个 "绕圈" 的过程（比如从
127转到-128，从0转到-1）。
第二个圈：无符号数（带 unsigned，比如 unsigned char）
- 范围是
0 ~ 255（8 位无符号数的范围）； - 圈也是循环的：比如
255再加 1，存不下了，会 "绕到"0；0再减 1，会 "绕到"255。 - 图里的箭头就是这个过程（比如从
255转到0）
不管是 10 进制、8 进制还是 16 进制的数字，计算机内部只会用 "二进制" 来存储
8 进制、16 进制是 ** 人类为了 "简化二进制的书写"** 搞出来的 "字符串写法"------ 因为二进制太长了，8/16 进制是给人看的、简化的字符串写法
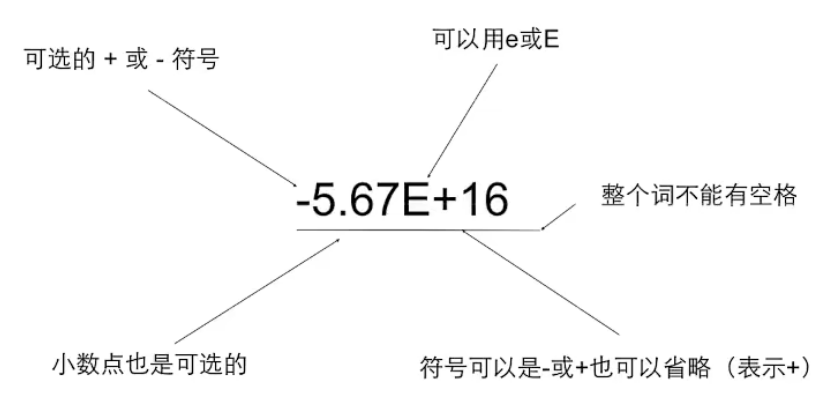
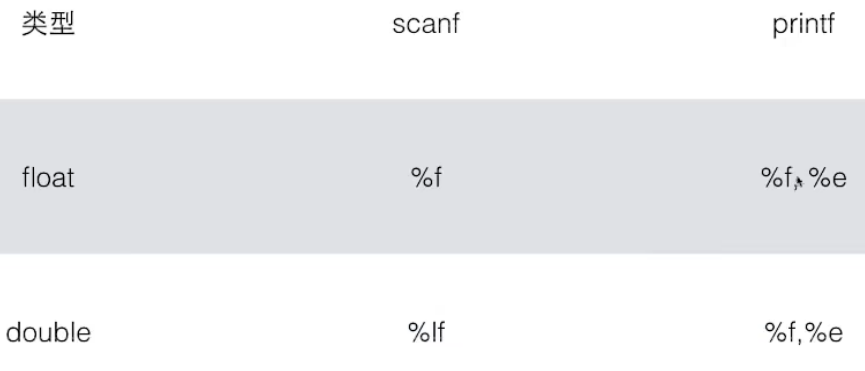e是科学计数
输出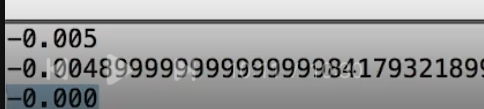
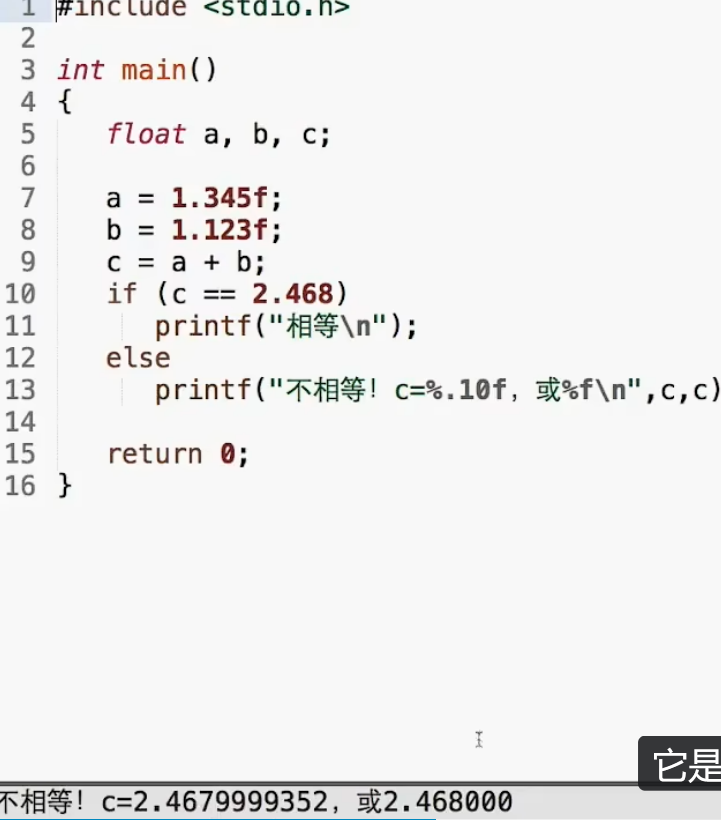左边是对的，因为浮点只有七位有效，这里输出10位
所以比如算钱的时候，不能用小数点误差会累积，需要换成整数
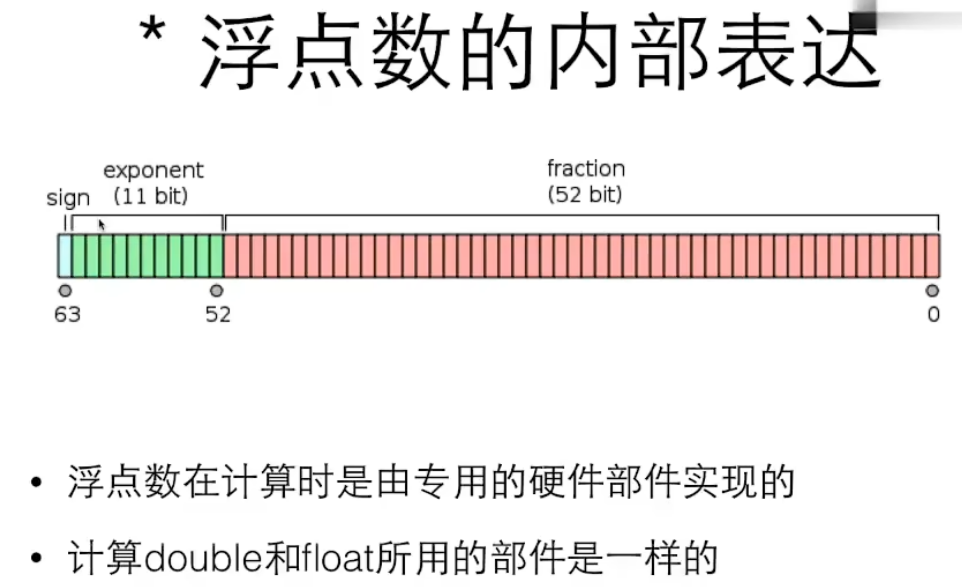
1个比特表达负数，11表达指数，后面的表示分数多少