接触点响应MATLAB有限元车桥耦合：可加不平整度与求解接触点响应

接触点响应MATLAB有限元车桥耦合可加不平整度可求解接触点响应（没有车辆响应的干扰，间接识别桥频效果更好）％可根据需要设置跳车冲击

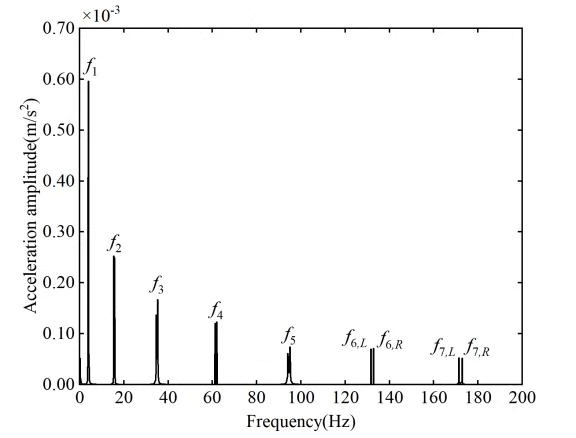
接触点响应分析在车辆与桥梁耦合系统中的应用是一个非常有趣的话题。通过有限元方法，我们可以在MATLAB中模拟车辆与桥梁之间的相互作用，从而更好地理解系统的动态特性。特别是在分析接触点响应时，我们可以忽略车辆自身的响应干扰，从而更准确地识别桥梁的固有频率和动态特性。

1. 车桥耦合系统的基本概念

车桥耦合系统指的是车辆和桥梁之间通过接触点（通常是车轮和桥面之间的接触点）相互作用的系统。这种耦合系统在实际工程中非常重要，因为它直接影响到车辆的行驶舒适性、桥梁的使用寿命以及系统的安全性。

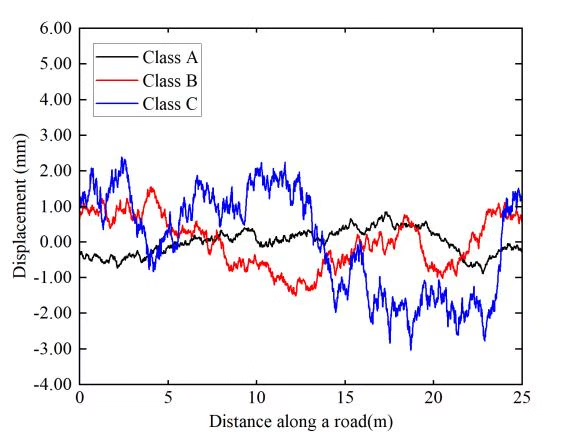
在MATLAB中，我们可以使用有限元方法来建模和分析这种耦合系统。有限元方法是一种强大的数值分析工具，能够将复杂的结构离散化为有限个单元，从而方便地进行数值计算和分析。

2. 接触点响应分析

接触点响应分析是车桥耦合系统分析中的一个关键部分。通过分析接触点的响应，我们可以了解车辆和桥梁之间的相互作用，从而优化设计和提高系统的性能。

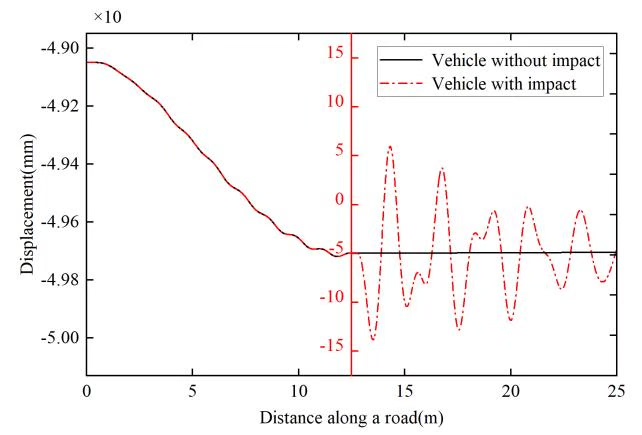
在MATLAB中，我们可以使用以下代码来定义接触点的响应：

matlab 复制代码

% 定义接触点的位置
contact_points = [10, 20, 30]; % 单位：米

% 定义接触点的刚度
stiffness = 1e6; % 单位：N/m

% 定义接触点的阻尼
damping = 1e4; % 单位：N·s/m

% 定义接触点的响应
response = zeros(length(contact_points), 1);

% 计算接触点的响应
for i = 1:length(contact_points)
    response(i) = stiffness * displacement(i) - damping * velocity(i);
end

这段代码定义了接触点的位置、刚度和阻尼，并计算了接触点的响应。通过这些参数，我们可以模拟车辆和桥梁之间的相互作用。

3. 不平整度的引入

在实际工程中，桥面的不平整度对车辆和桥梁的响应有着重要影响。通过引入不平整度，我们可以更准确地模拟实际的行驶条件。

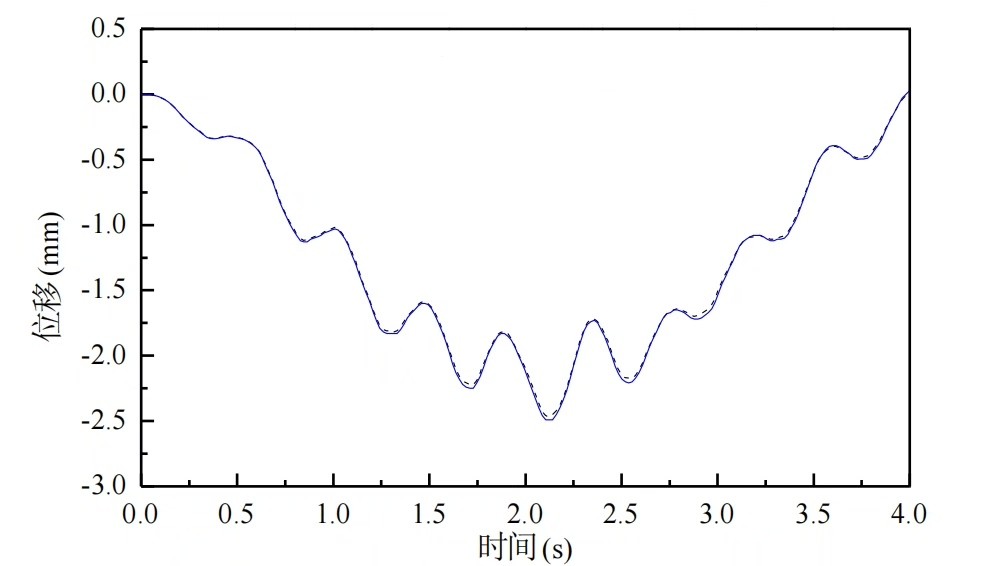
在MATLAB中，我们可以使用以下代码来引入不平整度：

matlab 复制代码

% 定义桥面的不平整度
roughness = 0.01; % 单位：米

% 定义不平整度的频率
frequency = 10; % 单位：Hz

% 定义不平整度的相位
phase = pi/2; % 单位：弧度

% 计算不平整度的影响
roughness_effect = roughness * sin(2*pi*frequency*time + phase);

这段代码定义了桥面的不平整度、频率和相位，并计算了不平整度对系统的影响。通过这些参数，我们可以模拟桥面不平整度对车辆和桥梁响应的影响。

4. 跳车冲击的设置

跳车冲击是车辆在行驶过程中可能遇到的一种极端情况。通过设置跳车冲击，我们可以模拟车辆在遇到障碍物或突然变化的路面时的响应。

在MATLAB中，我们可以使用以下代码来设置跳车冲击：

matlab 复制代码

% 定义跳车冲击的幅度
jump_amplitude = 0.5; % 单位：米

% 定义跳车冲击的时间
jump_time = 5; % 单位：秒

% 定义跳车冲击的相位
jump_phase = 0; % 单位：弧度

% 计算跳车冲击的影响
jump_effect = jump_amplitude * sin(2*pi*jump_time + jump_phase);

这段代码定义了跳车冲击的幅度、时间和相位，并计算了跳车冲击对系统的影响。通过这些参数，我们可以模拟车辆在遇到跳车冲击时的响应。

5. 结论

通过接触点响应分析，我们可以更好地理解车辆和桥梁之间的相互作用。在MATLAB中，我们可以方便地建模和分析这种耦合系统，并通过引入不平整度和跳车冲击来模拟实际的行驶条件。

这种方法不仅可以帮助我们优化设计，提高系统的性能，还可以为实际工程提供重要的参考价值。希望这篇博文能够帮助你更好地理解接触点响应分析在车辆与桥梁耦合系统中的应用。