文章目录
-
- 定义
- 为什么要引入波数这个变量
- [📌 1. 计算和表达更方便](#📌 1. 计算和表达更方便)
- [📌 2. 便于表示振动能级差](#📌 2. 便于表示振动能级差)
- [📌 3. 光谱绘图更合理](#📌 3. 光谱绘图更合理)
- [📌 4. 国际惯例](#📌 4. 国际惯例)
在光谱数据中,经常出现波数与波长两个单位,波长(λ )和波数(ν̅)是描述光的两种常用方式,它们可以互相转换。
AI生成,供参考
定义
- 波长 λ :光波的长度,常用单位是 nm(纳米) 或 cm(厘米)。
- 波数 ν̅ :每厘米有多少个波,数学上是波长的倒数,常用单位是 cm⁻¹。
波数 ν ˉ = 1 λ 波数 \bar{\nu} = \frac{1}{\lambda} 波数νˉ=λ1
为什么要引入波数这个变量
📌 1. 计算和表达更方便
- 波数和能量 、频率 是正比关系,比波长更直接反映光的能量。
- 在量子力学里,光子的能量是:
E = h ν = h c ν ˉ E = h\nu = h c \bar{\nu} E=hν=hcνˉ
其中:
- h 是普朗克常数
- c 是光速
因此,波数越大 → 光子能量越高,一看数值就能知道能量大小。
相比之下,如果用波长表示,能量和波长是反比关系(E=hc/λ),直觉上没那么方便。
📌 2. 便于表示振动能级差
在分子光谱学中,能级差常以 cm⁻¹ 表示,这样可以直接用"加减法"计算跃迁能量:
Δ ν ~ = ν ~ 2 − ν ~ 1 \Delta \tilde{\nu} = \tilde{\nu}_2 - \tilde{\nu}_1 Δν~=ν~2−ν~1
如果用波长表示,必须先取倒数再做运算,麻烦且不直观。
📌 3. 光谱绘图更合理
- 波数与频率成正比,绘制光谱时横轴是波数,峰的间隔与能级间隔直接对应。
- 如果用波长,横轴是非线性的(短波段挤在一起,长波段拉得很开),分析不方便。
📌 4. 国际惯例
在红外、拉曼、紫外可见光谱学里,波数是标准横轴单位。
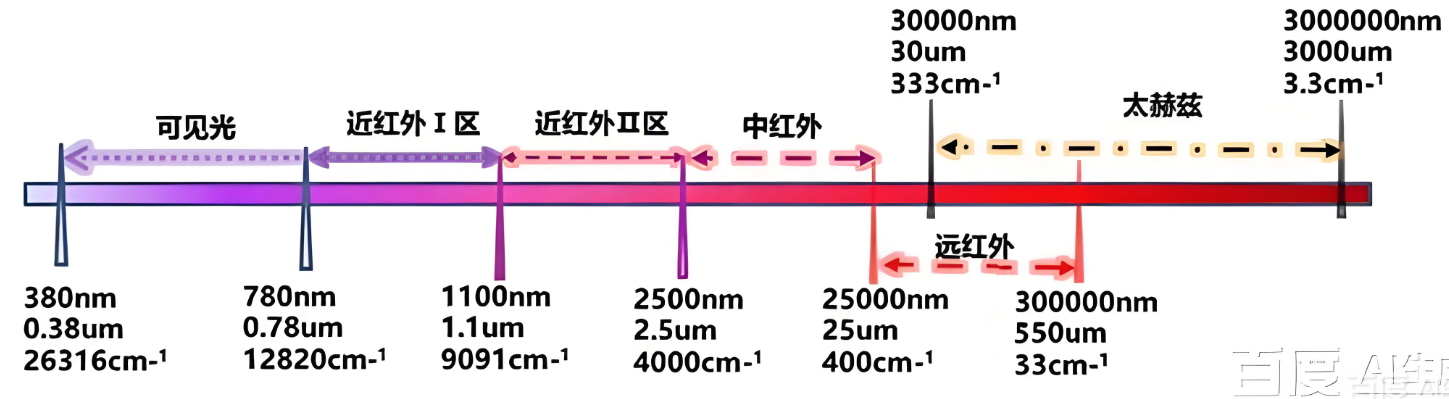
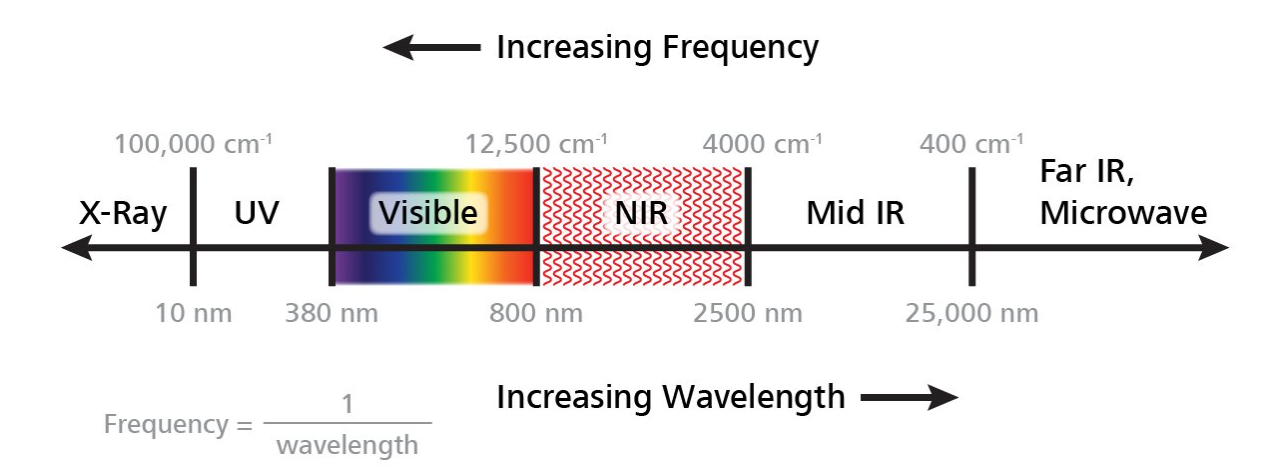
- 近红外光谱常用 4000--12800 cm⁻¹
- 中红外光谱常用 400--4000 cm⁻¹
- 这样可以直接拼接光谱,无需换算成波长再画图。