机器学习项目实战——鸢尾花大作战

一、项目概述

在这个实战项目中，我们将使用经典的鸢尾花数据集，通过Logistic回归模型来分类三种不同品种的鸢尾花。这是一个完美的机器学习入门项目，涵盖了数据加载、探索、预处理、模型训练和评估的完整流程。

二、加载数据集

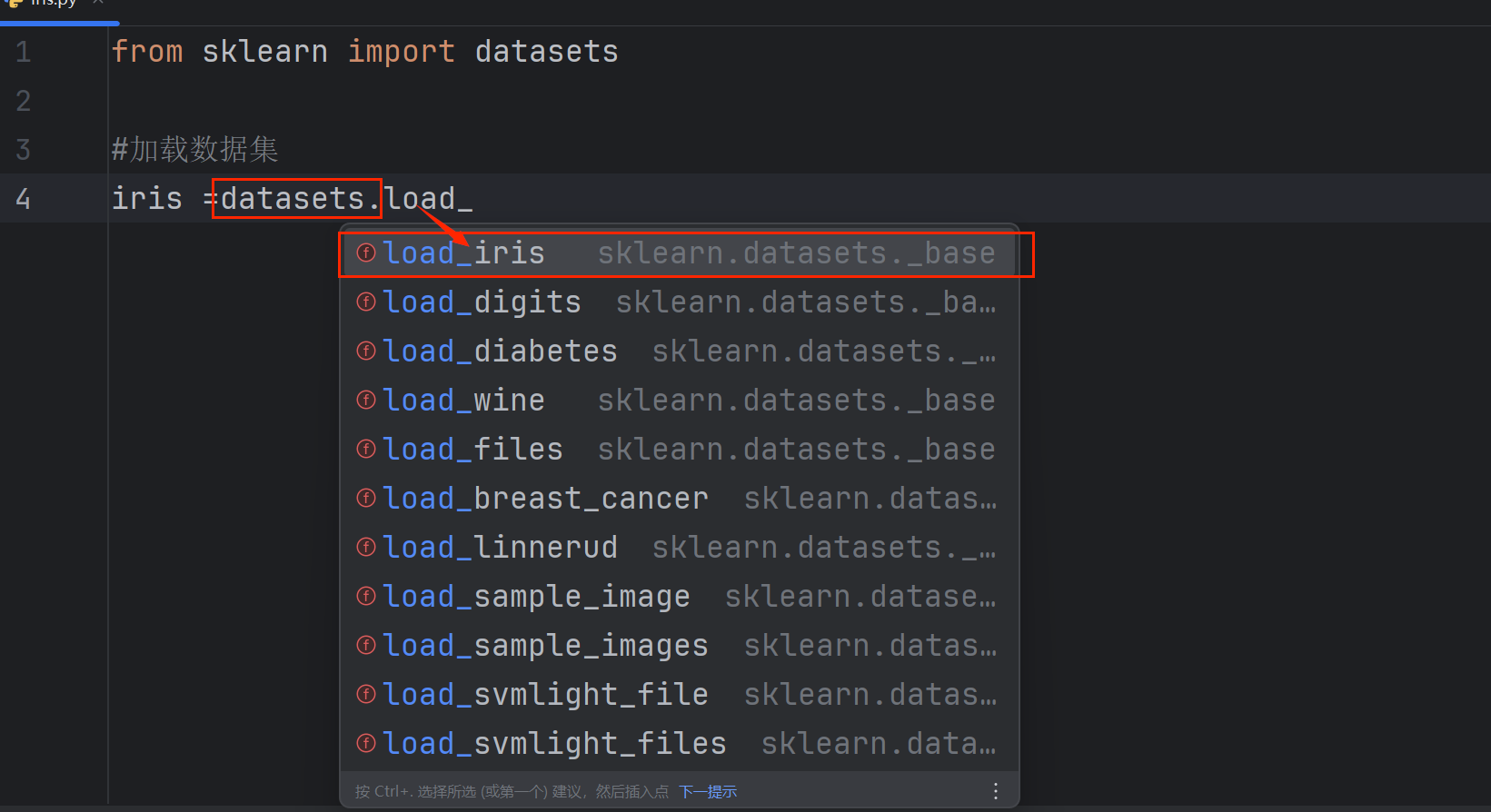
1.加载数据集

这是机器学习项目中最基础且关键的一步。

2.显示标签

y 在这个代码中代表的是目标变量 （target variable），也就是我们常说的标签 或输出。

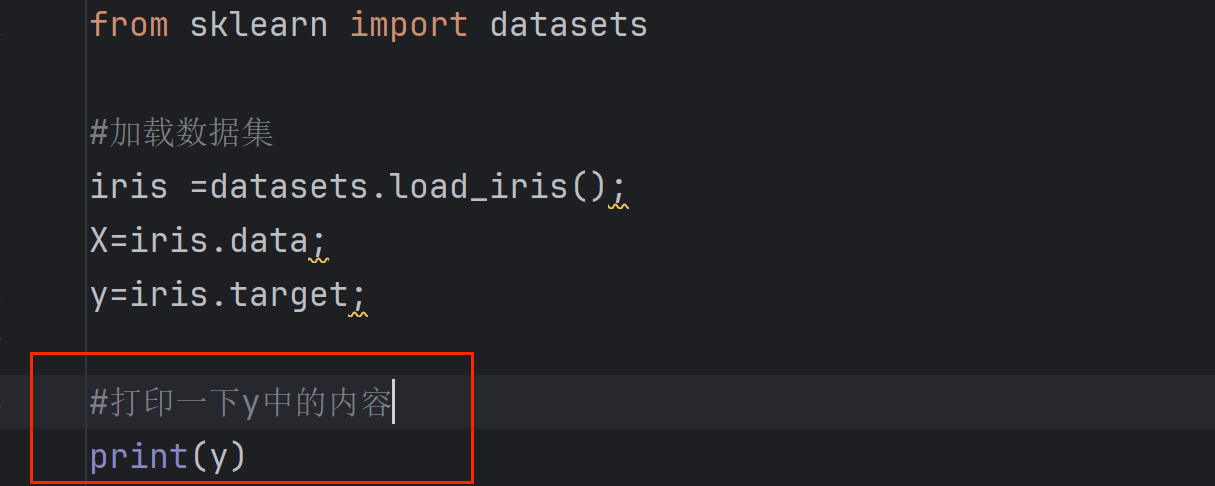
y中的内容为

在鸢尾花数据集中：

0 → 山鸢尾

1 → 变色鸢尾

2 → 维吉尼亚鸢尾

明显，它是一个多分类的数据集

3.小结

这段代码是鸢尾花分类项目的起点，为后续的数据预处理、模型训练和评估准备。理解这个基础步骤对于掌握完整的机器学习工作流程至关重要。

4.完整的代码

# 导入scikit-learn库中的datasets模块，该模块包含多个经典数据集
from sklearn import datasets

# 加载鸢尾花(Iris)数据集
# 这是一个经典的机器学习数据集，包含3种鸢尾花的测量数据
iris = datasets.load_iris()

# 获取特征数据，输入变量
# X包含4个特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度
# 形状为(150, 4)，表示150个样本，每个样本4个特征
X = iris.data

# 获取目标标签（输出变量）
# y包含每个样本对应的鸢尾花品种标签
# 0: 山鸢尾 1:变色鸢尾 2: 维吉尼亚鸢尾
y = iris.target

# 打印目标标签数组y的内容
# 这将显示一个包含150个元素的数组，元素值为0、1或2
# 用于直观了解数据分布和标签编码
print(y)

三、拆分数据集

1.导入sklearn.model_selection中的train_test_split模块

from sklearn.model_selection import train_test_split

2.使用train_test_split划分训练-测试数据

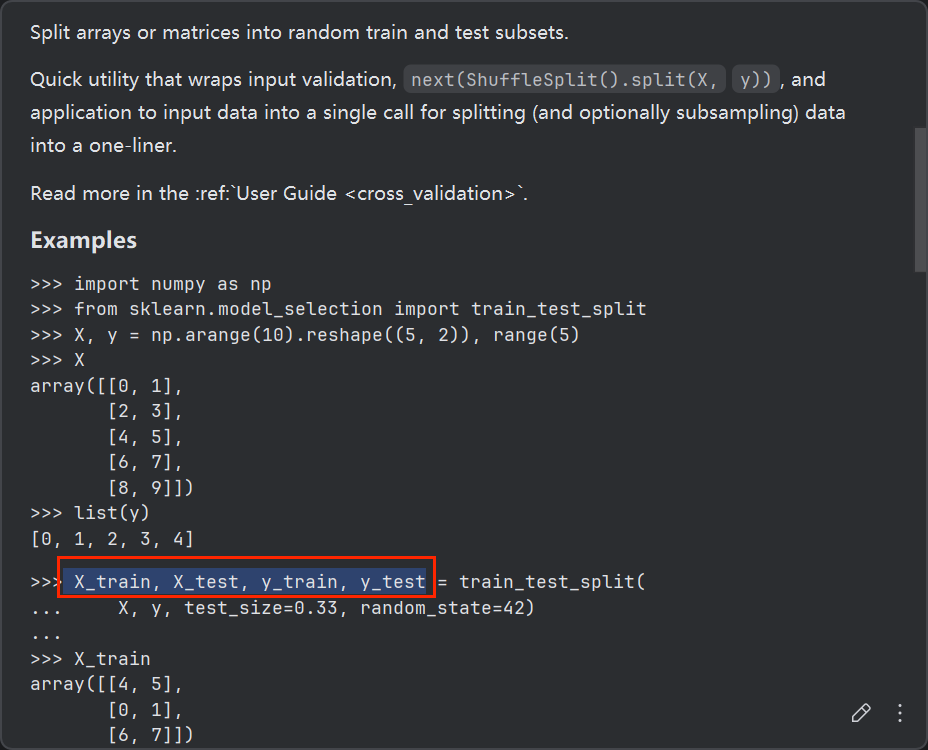
此处使用train_test_split()函数进行合理的训练-测试数据划分

将鼠标放置在train_test_split()上会显示如下的内容：

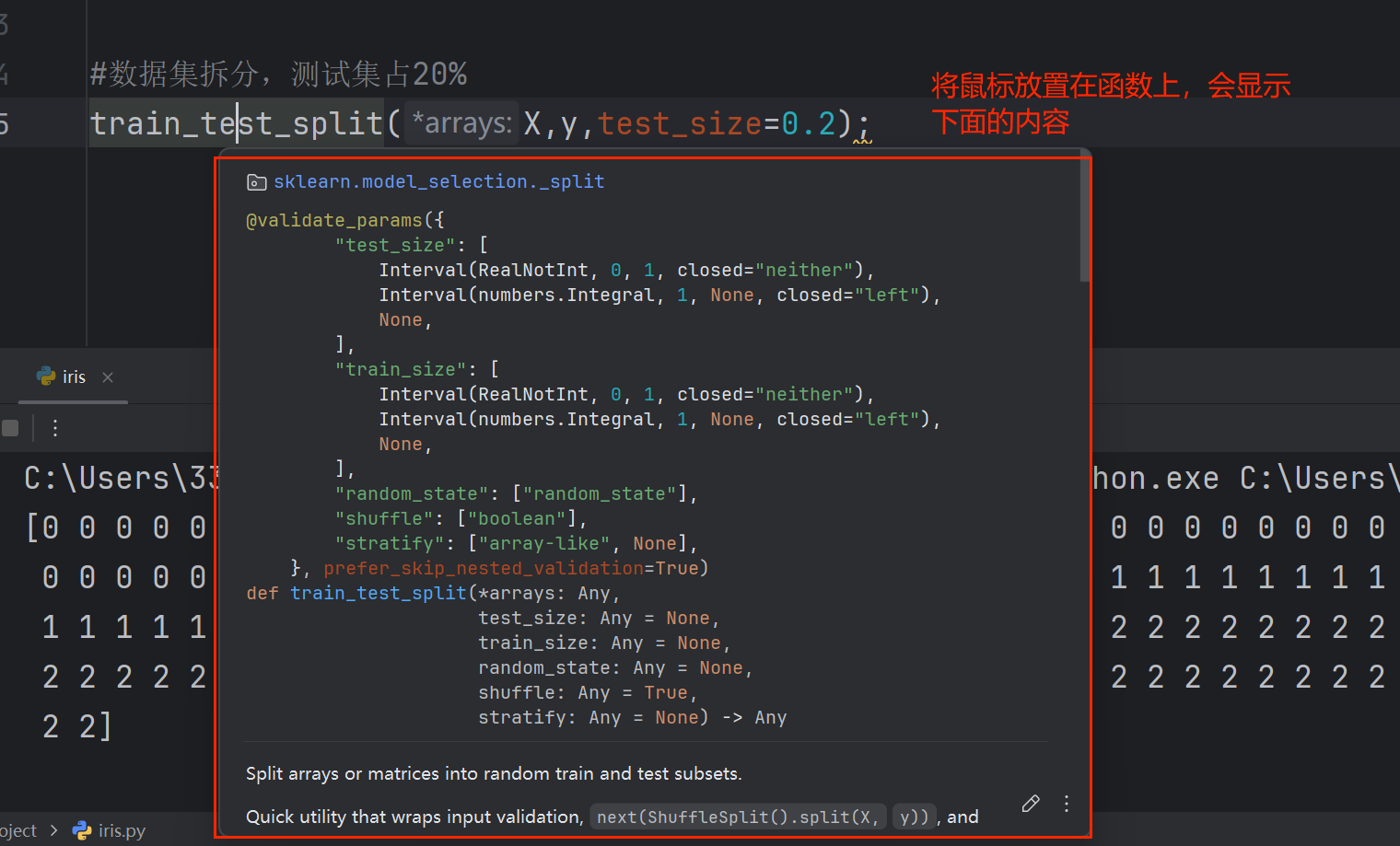
3.小经验分享

train_test_split返回的四个变量名X_train, X_test, y_train, y_test可以直接整行复制使用，避免重复输入相似的变量名。

4.完整的源代码+注释

# 导入scikit-learn库中的datasets模块，该模块包含多个经典数据集
from sklearn import datasets

# 导入train_test_split函数，用于将数据集划分为训练集和测试集
from sklearn.model_selection import train_test_split

# 加载鸢尾花(Iris)数据集
# 这是一个经典的机器学习数据集，包含3种鸢尾花的测量数据
iris = datasets.load_iris()

# 获取特征数据（输入变量）
# X包含4个特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度
# 形状为(150, 4)，表示150个样本，每个样本4个特征
X = iris.data

# 获取目标标签（输出变量）
# y包含每个样本对应的鸢尾花品种标签
# 0: setosa(山鸢尾), 1: versicolor(变色鸢尾), 2: virginica(维吉尼亚鸢尾)
# 形状为(150,)，表示150个样本对应的类别
y = iris.target

# 打印目标标签数组y的内容
# 这将显示一个包含150个元素的数组，元素值为0、1或2
# 用于直观了解数据分布和标签编码
print(y)

# 将完整数据集划分为训练集和测试集
# X_train, y_train: 用于模型训练的特征和标签
# X_test, y_test: 用于模型评估的特征和标签
# test_size=0.2: 指定测试集占总数据集的20%，训练集占80%
# 随机种子未设置，每次运行划分结果可能不同
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

四、创建逻辑回归对象

1.导入LogisticRegression模块

from sklearn.linear_model import LogisticRegression

2.创建逻辑回归对象

lr = LogisticRegression();

3.multi_class参数介绍

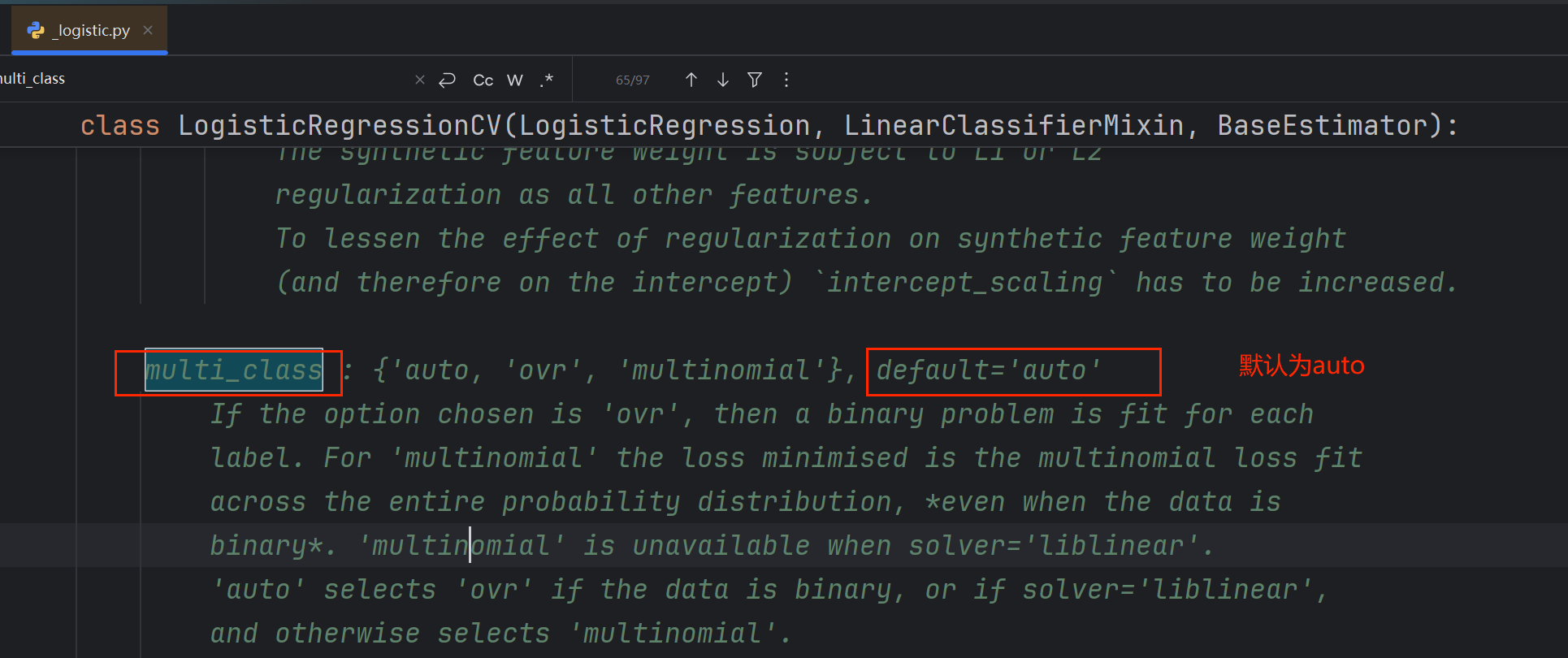
multi_class 参数用于指定逻辑回归处理多分类问题时的策略，有三个可选值：

1)'ovr'：

为每个类别训练一个二分类器，将该类别与其他所有类别区分开

2)'multinomial'：

直接处理多分类问题，最小化多项损失函数，即使数据是二分类的也会使用此方法

3)'auto':

如果数据是二分类或使用 solver='liblinear'，则选择 'ovr';

其他情况下选择 'multinomial';

对于参数的选择，通常有如下的建议：

**1)**对于二分类问题，两种策略效果相似对于

2) 多分类问题，'multinomial' 通常能提供更准确的概率估计

3)如果不确定，使用默认的 'auto' 通常是最安全的选择

4.选择参数

由二中的2可知，鸢尾花的数据集是一个多分类的数据集。

由此，我们可以设置参数。

lr = LogisticRegression(multi_class='multinomial');

5.完整的代码+注释

# 导入scikit-learn库中的datasets模块，该模块包含多个经典数据集
from sklearn import datasets

# 导入train_test_split函数，用于将数据集划分为训练集和测试集
from sklearn.model_selection import train_test_split

# 导入LogisticRegression类，用于创建逻辑回归分类模型
from sklearn.linear_model import LogisticRegression

# 加载鸢尾花数据集
# 这个数据集包含3种不同品种鸢尾花的测量数据
iris = datasets.load_iris()

# 获取特征数据 - 花瓣和花萼的尺寸测量值
X = iris.data

# 获取目标标签 - 每朵花对应的品种（0=山鸢尾，1=变色鸢尾，2=维吉尼亚鸢尾）
y = iris.target

# 打印目标标签，查看数据中包含哪些品种
print(y)

# 将数据分成训练集和测试集
# 80%的数据用于训练模型，20%的数据用于测试模型效果
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 创建一个逻辑回归分类器
# multi_class='multinomial'表示使用多分类方法处理3种花的问题
lr = LogisticRegression(multi_class='multinomial')

6.小结

简单说，这段代码就是为后续训练一个能识别鸢尾花品种的AI模型做好了所有前期准备，接下来只要把训练数据"喂"给模型学习就行了。

五、训练模型

1.导入accuracy_score函数

导入accuracy_score函数，用于计算模型预测的准确率

from sklearn.metrics import accuracy_score

2.训练逻辑回归模型

使用训练数据训练逻辑回归模型，模型会学习如何根据花的特征来识别花的品种

lr.fit(X_train,y_train)

3.完整的代码+注释

# 导入scikit-learn库中的datasets模块，该模块包含多个经典数据集
from sklearn import datasets

# 导入train_test_split函数，用于将数据集划分为训练集和测试集
from sklearn.model_selection import train_test_split

# 导入LogisticRegression类，用于创建逻辑回归分类模型
from sklearn.linear_model import LogisticRegression

# 导入accuracy_score函数，用于计算模型预测的准确率
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
# 这个数据集包含3种不同品种鸢尾花的测量数据
iris = datasets.load_iris()

# 获取特征数据 - 花瓣和花萼的尺寸测量值
X = iris.data

# 获取目标标签 - 每朵花对应的品种（0=山鸢尾，1=变色鸢尾，2=维吉尼亚鸢尾）
y = iris.target

# 打印目标标签，查看数据中包含哪些品种
print(y)

# 将数据分成训练集和测试集
# 80%的数据用于训练模型，20%的数据用于测试模型效果
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 创建一个逻辑回归分类器
# multi_class='multinomial'表示使用多分类方法处理3种花的问题
lr = LogisticRegression(multi_class='multinomial')

# 使用训练数据训练逻辑回归模型
# 模型会学习如何根据花的特征（花瓣、花萼尺寸）来识别花的品种
lr.fit(X_train, y_train)

4.小结

这段代码完成了一个AI模型的完整训练过程 ，让模型学会了如何根据花的尺寸特征来识别三种不同的鸢尾花品种。接下来就可以用考试卷（测试集）来检验这个模型学得好不好了。

六、预测

1.使用训练好的模型对测试集进行预测

使用训练好的模型对测试集进行预测，模型会根据学习到的规律，预测测试集中每朵花的品种。

y_pred = lr.predict(X_test)

2.打印准确率

准确率表示模型预测正确的比例，是评估模型性能的重要指标。

print("准确率：%.2f" % accuracy_score(y_test, y_pred))

3.完整的代码+注释

# 导入scikit-learn库中的datasets模块，该模块包含多个经典数据集
from sklearn import datasets

# 导入train_test_split函数，用于将数据集划分为训练集和测试集
from sklearn.model_selection import train_test_split

# 导入LogisticRegression类，用于创建逻辑回归分类模型
from sklearn.linear_model import LogisticRegression

# 导入accuracy_score函数，用于计算模型预测的准确率
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
# 这个数据集包含3种不同品种鸢尾花的测量数据
iris = datasets.load_iris()

# 获取特征数据 - 花瓣和花萼的尺寸测量值
X = iris.data

# 获取目标标签 - 每朵花对应的品种（0=山鸢尾，1=变色鸢尾，2=维吉尼亚鸢尾）
y = iris.target

# 打印目标标签，查看数据中包含哪些品种
print(y)

# 将数据分成训练集和测试集
# 80%的数据用于训练模型，20%的数据用于测试模型效果
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 创建一个逻辑回归分类器
# multi_class='multinomial'表示使用多分类方法处理3种花的问题
lr = LogisticRegression(multi_class='multinomial')

# 使用训练数据训练逻辑回归模型
# 模型会学习如何根据花的特征（花瓣、花萼尺寸）来识别花的品种
lr.fit(X_train, y_train)

# 使用训练好的模型对测试集进行预测
# 模型会根据学习到的规律，预测测试集中每朵花的品种
y_pred = lr.predict(X_test)

# 计算并显示模型在测试集上的准确率
# 准确率表示模型预测正确的比例，是评估模型性能的重要指标
print("准确率：%.2f" % accuracy_score(y_test, y_pred))

4.小结

这段代码完整地演示了如何训练一个AI模型来识别鸢尾花品种，并且评估它的识别准确率。通过这个流程，我们可以知道这个模型是否真的学会了识别不同品种的鸢尾花，以及它的识别能力有多强。

七、最终的预测结果

八、常见问题

1.没有安装scikit-learn库

在PyCharm中运行from sklearn import datasets，如果出现红色波浪线或运行报错，说明scikit-learn库未安装。

如果没有这个scikit-learn库，我们使用里面的函数将会出现如下的情况：

如果运行代码，将会出现下面的结果：

当遇到ModuleNotFoundError: No module named 'sklearn'错误时，不要慌张，这是机器学习入门最常见的问题之一。

出现这个情况的原因是：没有安装scikit-learn库

如何解决这个问题呢？

1).在终端中输入如下的指令，以检查scikit-learn库是否存在。

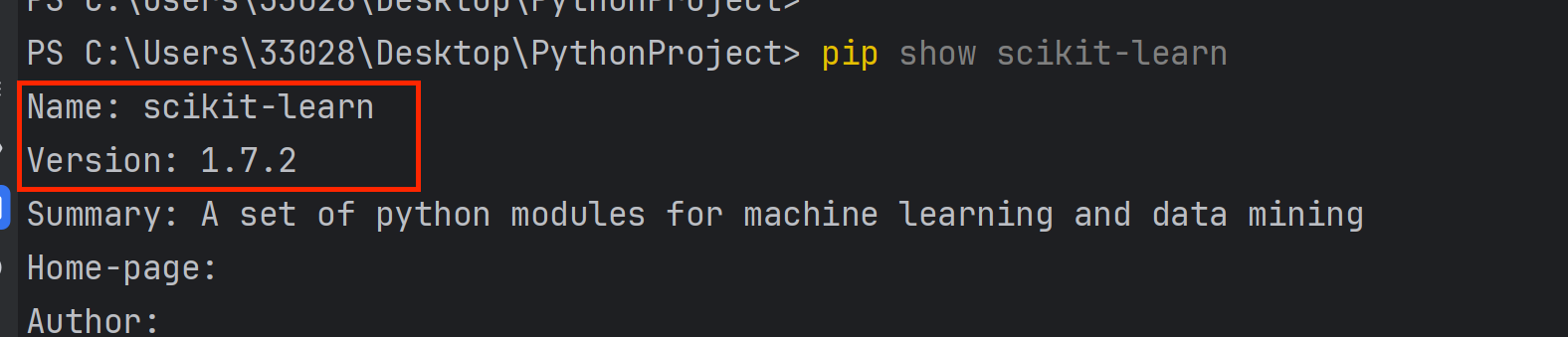
pip show scikit-learn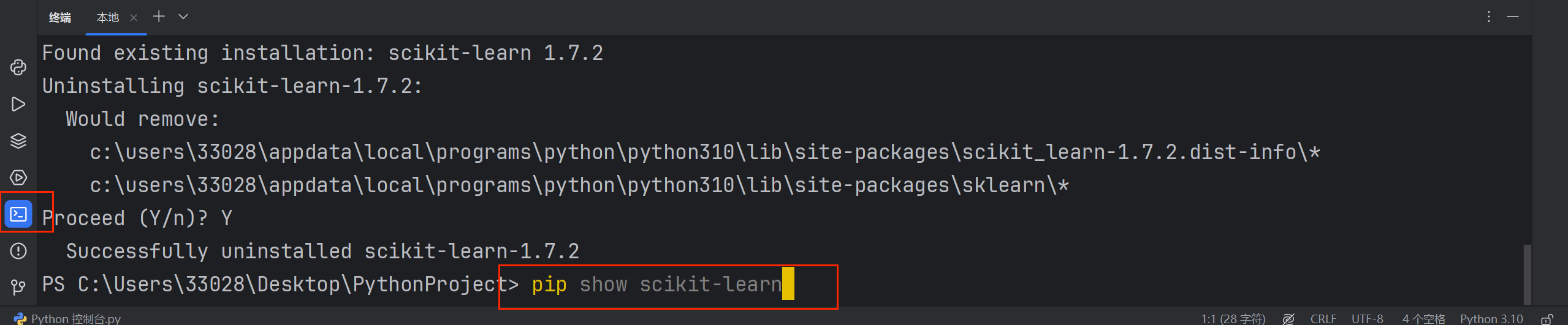   

运行终端，出现如下的结果，表示没有下载scikit-learn库。

2).下载scikit-learn库

在终端使用的命令：

pip install scikit-learn

敲下回车后，显示如下的内容，表示下载成功。

3)可使用如下的命令检查scikit-learn库是否安装成功：

 pip show scikit-learn

如下的界面信息告诉我们scikit-learn库存在，并且告诉了我们scikit-learn库相应的版本号。