K-D Tree 相关

rgw20102025-12-01 12:18

部分发表于洛谷。

简介：

K-D Tree 是一种适用于 \(k\) 维空间信息处理的数据结构，一般是维护 \(n\) 个点的信息，建出平衡二叉树；在 \(k\) 比较小的

建树：

一般使用交替建树，递归的分为以下三个步骤：

  • 交替 选择一个维度切割（即 \(x, y, z, \cdots\) 依次切一遍，最后回到 \(x\) 继续切）。

  • 选择一个切割点将这个维度切割了。

  • 然后递归到被切割点切开的两个超立方体继续切割，直到区域内没有点。

一个切割点的左右儿子是其切开的两个超立方体的切割点。

为了维持二叉树的平衡，要左右子树尽量均匀，所以一般选择这个切割维度的中位数作为切割点。

此时得到的树高显然是 \(\log n + O(1)\) 级别的。

为了方便理解，给定一个在二维平面的例子：

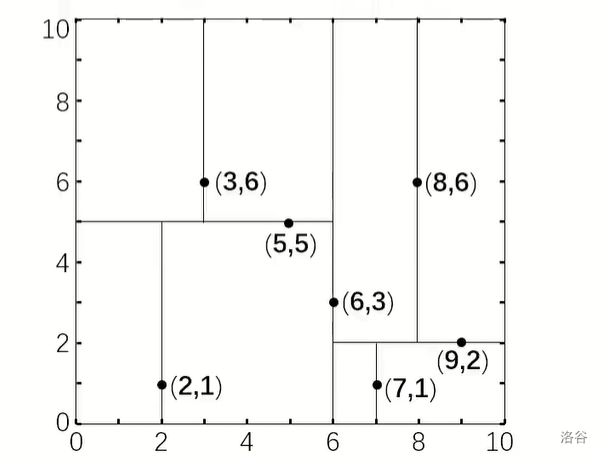
此时建出的 K-D Tree 就是：

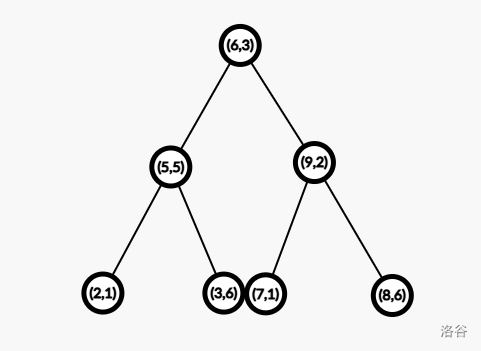
可以使用 nth_element 辅助建树，时间复杂度为 \(O(n \log n)\)。

为了方便操作，对于每个点，可以维护其被切割时的超立方体，即可以记录其子树内每个维度的最大最小值。

最近点对：

即对于每个点，求出到其它点的最短距离。

设查询点是 \(a\)，依然是递归的形式的从 \(rt\) 进入（设当前到了 \(p\)）：

  • 先用 \(\operatorname{dis}(a, p)\) 更新答案 \(ans\)。

  • 然后求出 \(p\) 到左右子树所代表的超立方体的最短距离 \(disl, disr\)，如果大于 \(ans\)，则直接剪枝。

  • 否则进入 \(disl, disr\) 更小的那个子树先更新，出来时再判断是否比另外一个更优；这是估价型剪枝。

提示： 使用 K-D Tree 单次查询最坏是 \(O(N)\) 的，但是如果没有特意卡的情况下，还是可以骗到很多分的。

操作：

对于一个高维矩形 \(Q\) 内的点的查询，可以递归式的从 \(rt\) 开始判断（设当前到了 \(p\)）：

  • 若包含 \(p\) 子树，则直接返回所有点的信息。

  • 若与 \(p\) 子树所在超立方体有交，先考虑 \(p\) 本身的贡献，然后递归到左右子树处理。

  • 否则无交，直接退出。

考虑时间复杂度分析，先考虑二维情况，根据递归，显然时间复杂度是跟与 \(Q\) 相交的点（且没有被 \(Q\) 包含）的数量，将这些点分为两类：

  • 完全包含 \(Q\)：即树上一条到根的链，点数是 \(O(h) = O(\log n)\) 的。

  • 部分与 \(Q\) 相交：显然这些点所代表的矩形互不相交。

考虑求与 \(Q\) 相交的矩形的数量，显然这些与 \(Q\) 相交的矩形必然至少与一条 \(Q\) 的边相交；于是可以转化为与一条边相交的矩形的数量：

  • 考虑一个点 \(p\) 所代表的矩形，通过两次切割将这个矩形分为了四个部分，每个部分为 \(p\) 的孙子来表示，而一条平行于坐标轴的直线显然最多穿越这个四个部分中的两个部分。

这里阐述了要交替维度切割建树的原因，因为如果不交替切割，一条直线可能会直接穿过这四个部分。

因为子树大小几乎是严格的一半，于是可以得到递推式子：

\[T(n) = 2T(\frac{n}{4}) + O(1) \]

得到 \(T(n) = \sqrt n\)；拓展到 \(k\) 维上，类似的，是 \(T(n) = 2^{k - 1} T(\frac{n}{2^k}) + O(1)\)，于是 \(T(n) = O(n^{1 - \frac{1}{k}})\)（这里是将 \(k\) 当做常数计算的，实际上常数要大不少）。

插入/删除：

先说删除，比较简单，不需要真的将这个点删除，就把这个点打上懒标记，将其贡献清除即可，时间复杂度是 \(O(h) = O(\log n)\) 的；如果要真删的话，也可以用下面的重构方法。

如果直接插入，就是递归式的，根据是否在左右子树的超立方体内判断插入到哪里，最后到达空节点。

但是这样可能会导致二叉树不平衡，使得查询复杂度出错；然后大家可能会想到替罪羊树的方法，定义一个平衡因子 \(\alpha\)，如果子树大小超了，就子树重构，可以保证树高是 \(O(\log n)\) 的。

但是请注意，复杂度分析中，其四个孙子最多只有两个孙子被算进去，同时根据儿子子树严格减半，可以得到递推式；而替罪羊树的方法，只保证了树高是 \(O(\log n)\) 的，没有保证子树节点数量，所以若那条 \(Q\) 中的线恰好穿过四个孙子中两个子树最大的孙子，复杂度将会被卡满出问题，具体复杂度不太清楚，但是应该能卡？

于是可以想到两种著名的重构算法：

  • 根号重构。

  • 二进制分组。

根号重构，即我每插入 \(B\) 个点后再重构，存下插入的点，每次查询是 \(O(B + n^{1 - \frac{1}{k}})\) 的；重构 \(\frac{n}{B}\) 次，复杂度是 \(O(\frac{n^2 \log n}{B})\)，均摊下来单次插入复杂度是 \(O(\frac{n \log n}{B})\)，取 \(B = \sqrt{n \log n}\) 最优；插入复杂度是 \(O(\sqrt{n \log n})\)，查询 \(O(\sqrt{n \log n} + n^{1 - \frac{1}{k}})\)；常数一般，可以使用。

二进制分组，即将 \(n\) 二进制拆分，维护若干个二次幂大小的 K-D Tree；每次新加一个点，即新建一个大小 \(2^0\) 的 K-D Tree，然后不断将相同大小的树合并（实现时把所有需要合并的点，全部拿出来合并即可，而不是真的依次合并，这样过于浪费）；因为合并带 \(\log\)，所以最后均摊复杂度是 \(O(n \log^2 n)\) 的；查询就是在每个树上查一遍，最后累加起来，是一个等比数列累加的形式，也是 \(O(n^{1 - \frac{1}{k}})\) 的；常数很小。

例题：P4148 简单题

题意：

二维平面上，单点加，区间矩形查；强制在线。

思路：

板子题，使用上面任意一种重构方式即可通过。

code

P14312 【模板】K-D Tree

题意：

\(k\) 维平面上，动态插入点，高维矩形内的点加，高维矩形内的点查。

思路：

重构使用二进制分组形式。

对于高维矩形内的点加，使用懒标记维护即可，注意懒标记的下传等。

时间复杂度是 \(O(m \log^2 m + qm^{1 - \frac{1}{k}})\)。

完整代码：

cpp 复制代码 
#include<bits/stdc++.h>
#define lowbit(x) x & (-x)
#define pi pair<ll, ll>
#define ls(k) k << 1
#define rs(k) k << 1 | 1
#define fi first
#define se second
using namespace std;
typedef __int128 __;
typedef long double lb;
typedef double db;
typedef unsigned long long ull;
typedef long long ll;
const int N = 1.5e5 + 10, M = 18, K = 3;
inline ll read(){
	ll x = 0, f = 1;
	char c = getchar();
	while(c < '0' || c > '9'){
		if(c == '-')
			f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9'){
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return x * f;
}
inline void write(ll x){
	if(x < 0){
		putchar('-');
		x = -x;
	}
	if(x > 9)
		write(x / 10);
	putchar(x % 10 + '0');
}
ll ans;
int n, m, op, w, rk, nowk, cnt;
int h[N], rt[M];
struct point{
	ll X[K];
	point(){
		memset(X, 0, sizeof(X));
	}
	inline bool operator<(const point&rhs)const{
		return X[nowk] < rhs.X[nowk];
	}
}a;
struct KD_Node{
	point a, mn, mx;
	int siz, lson, rson;
	ll data, sum, tag;
	inline bool operator<(const KD_Node&rhs)const{
		return a < rhs.a;
	}
}Q, T[N];
inline void getmin(ll &x, ll y){
	x = (x < y) ? x : y;
}
inline void getmax(ll &x, ll y){
	x = (x > y) ? x : y;
}
inline void pushup(int k){
	T[k].siz = T[T[k].lson].siz + 1 + T[T[k].rson].siz;
	T[k].sum = T[k].data + T[T[k].lson].sum + T[T[k].rson].sum;
	for(int i = 0; i < rk; ++i){
		T[k].mn.X[i] = T[k].mx.X[i] = T[k].a.X[i];
		if(T[k].lson){
			getmin(T[k].mn.X[i], T[T[k].lson].mn.X[i]);
			getmax(T[k].mx.X[i], T[T[k].lson].mx.X[i]);
		}
		if(T[k].rson){
			getmin(T[k].mn.X[i], T[T[k].rson].mn.X[i]);
			getmax(T[k].mx.X[i], T[T[k].rson].mx.X[i]);			
		}
	}
}
inline void add(int k, ll v){
	if(!k)
	  return ;
	T[k].data += v;
	T[k].tag += v;
	T[k].sum += v * T[k].siz;
}
inline void push_down(int k){
	if(T[k].tag){
		add(T[k].lson, T[k].tag);
		add(T[k].rson, T[k].tag);
		T[k].tag = 0;
	}
}
inline int build(int l, int r, int k){
	if(l > r)
	  return 0;
	nowk = k;
	int mid = (l + r) >> 1;
	nth_element(h + l, h + mid, h + r + 1, [](int x, int y) {return T[x] < T[y];});
	k = (k + 1) % rk;
	T[h[mid]].lson = build(l, mid - 1, k);
	T[h[mid]].rson = build(mid + 1, r, k);
	pushup(h[mid]);
	return h[mid];
}
inline void reset(int &k){
	if(!k)
	  return ;
	h[++cnt] = k;
	push_down(k);
	reset(T[k].lson);
	reset(T[k].rson);
	k = 0;
}
inline ll query(int k){
	if(!k)
	  return 0;
	bool flag = 1;
	for(int i = 0; i < rk; ++i)
	  flag &= (Q.mn.X[i] <= T[k].mn.X[i] && T[k].mx.X[i] <= Q.mx.X[i]);
	if(flag)
	  return T[k].sum;
	for(int i = 0; i < rk; ++i)
	  if(Q.mx.X[i] < T[k].mn.X[i] || T[k].mx.X[i] < Q.mn.X[i])
		return 0;
	flag = 1;
	for(int i = 0; i < rk; ++i)
	  flag &= (Q.mn.X[i] <= T[k].a.X[i] && T[k].a.X[i] <= Q.mx.X[i]);
	ll sum = 0;
	if(flag)
	  sum = T[k].data;
	push_down(k);
	sum += query(T[k].lson);
	sum += query(T[k].rson);
	return sum;
}
inline void upd(int k, ll v){
	if(!k)
	  return;
	bool flag = 1;
	for(int i = 0; i < rk; ++i)
	  flag &= (Q.mn.X[i] <= T[k].mn.X[i] && T[k].mx.X[i] <= Q.mx.X[i]);
	if(flag){
		add(k, v);
		return ;
	}
	for(int i = 0; i < rk; ++i)
	  if(Q.mx.X[i] < T[k].mn.X[i] || T[k].mx.X[i] < Q.mn.X[i])
		return ;
	flag = 1;
	for(int i = 0; i < rk; ++i)
	  flag &= (Q.mn.X[i] <= T[k].a.X[i] && T[k].a.X[i] <= Q.mx.X[i]);
	if(flag)
	  T[k].data += v;
	push_down(k);
	upd(T[k].lson, v);
	upd(T[k].rson, v);
	pushup(k);
}
int main(){
//	freopen("A.in", "r", stdin);
	rk = read(), m = read();
	while(m--){
		op = read();
		if(op == 1){
			for(int i = 0; i < rk; ++i)
			  a.X[i] = read() ^ ans;
			w = read() ^ ans;
			T[++n] = {a, a, a, 0, 0, 0, w, w, 0};
			cnt = 0;
			h[++cnt] = n;
			for(int i = 0; i < M; ++i){
				if(!rt[i]){
					rt[i] = build(1, cnt, 0);
					break;
				}
				else
				  reset(rt[i]);
			}
		}
		else if(op == 2){
			for(int i = 0; i < rk; ++i)
			  a.X[i] = read() ^ ans;
			Q.mn = a;
			for(int i = 0; i < rk; ++i)
			  a.X[i] = read() ^ ans;	
			Q.mx = a;
			w = read() ^ ans;
			for(int i = 0; i < M; ++i)
			  if(rt[i])
				upd(rt[i], w);
		}
		else if(op == 3){
			for(int i = 0; i < rk; ++i)
			  a.X[i] = read() ^ ans;
			Q.mn = a;
			for(int i = 0; i < rk; ++i)
			  a.X[i] = read() ^ ans;	
			Q.mx = a;
			ans = 0;
			for(int i = 0; i < M; ++i)
			  if(rt[i])
				ans += query(rt[i]);
			write(ans);
			putchar('\n');
		}
		else
		  break;
	}
	return 0;
}
相关推荐
惆怅客1234 个月前
UVa12389/LA5821 Cybercrime Donut Investigation
树状数组·icpc·uva·k-d tree
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05Linux下V2Ray安装配置指南06【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连0746个Nano-banana 精选提示词，持续更新中08全球最强模型Grok4，国内已可免费使用！（附教程）09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）10“我的电脑”图标没了怎么办 4种方法找回