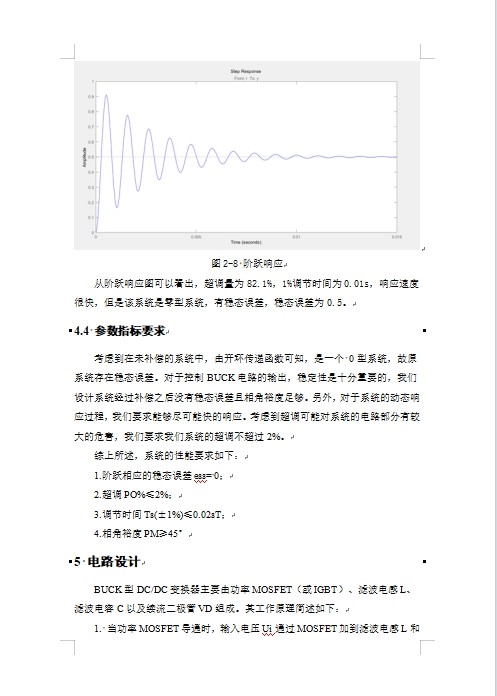
基于MATLAB的BUCK型DC/DC变换器系统设计：满足稳态误差、超调与相角裕度要求的系统参...

基于MATLAB的BUCK型DC/DC变换器系统设计 本设计包括设计报告，仿真程序。 参数指标要求 考虑到在未补偿的系统中，由开环传递函数可知，是一个 0型系统，故原系统存在稳态误差。 对于控制BUCK电路的输出，稳定性是十分重要的，我们设计系统经过补偿之后没有稳态误差且相角裕度足够。 另外，对于系统的动态响应过程，我们要求能够尽可能快的响应。 考虑到超调可能对系统的电路部分有较大的危害，我们要求我们系统的超调不超过2%。 综上所述，系统的性能要求如下： 1.阶跃相应的稳态误差ess= 0； 2.超调PO%≤2%； 3.调节时间Ts(±1%)≤0.02sT； 相角裕度PM≥45°

在设计BUCK型DC/DC变换器时，MATLAB是一个非常强大的工具，尤其是在系统仿真和控制器设计方面。今天我们就来聊聊如何用MATLAB设计一个满足特定性能要求的BUCK电路控制系统。

首先，我们得明确系统的性能要求：稳态误差为零，超调不超过2%，调节时间小于0.02秒，相角裕度至少45度。这些指标听起来有点吓人，但别担心，MATLAB会帮我们搞定。

开环系统分析

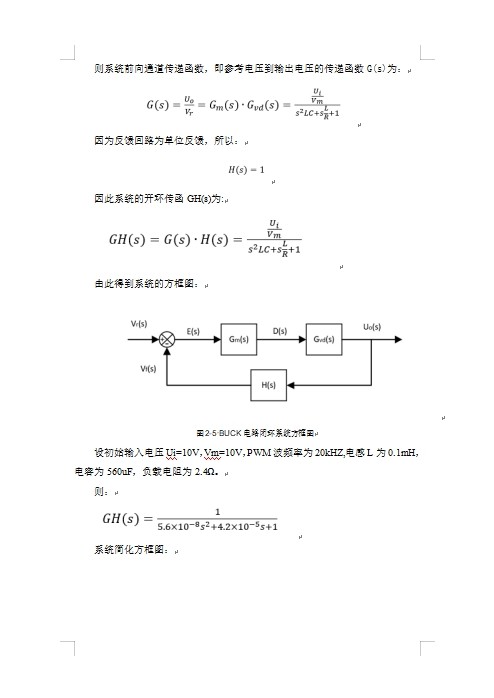
我们先从开环系统开始。BUCK电路的开环传递函数通常是一个0型系统，这意味着它会有稳态误差。我们可以用MATLAB来验证这一点。假设我们已经有了开环传递函数G(s)，我们可以用以下代码来绘制Bode图：

s = tf('s');
G = 1 / (s^2 + 2*s + 1); % 假设的开环传递函数
bode(G);
grid on;

从Bode图中，我们可以看到系统的相位裕度和增益裕度。如果相位裕度不够，系统就会不稳定，这是我们不希望的。

控制器设计

为了消除稳态误差并提高系统的动态响应，我们需要设计一个补偿器。常用的补偿器有PI控制器和PID控制器。这里我们选择PI控制器，因为它可以消除稳态误差。

Kp = 1; % 比例增益
Ki = 10; % 积分增益
C = Kp + Ki/s; % PI控制器

接下来，我们将控制器与开环系统串联，形成闭环系统：

T = feedback(C*G, 1); % 闭环系统
step(T); % 绘制阶跃响应
grid on;

通过调整Kp和Ki的值，我们可以优化系统的响应。目标是使超调不超过2%，调节时间小于0.02秒。

性能验证

为了验证系统是否满足性能要求，我们可以使用MATLAB的stepinfo函数来获取系统的阶跃响应信息：

info = stepinfo(T);
disp(info);

stepinfo会返回超调量、调节时间等信息。如果超调量超过2%，我们可以继续调整Kp和Ki，直到满足要求。

相角裕度检查

最后，我们需要检查系统的相角裕度是否至少为45度。我们可以使用margin函数来获取系统的相位裕度和增益裕度：

[Gm, Pm, Wcg, Wcp] = margin(C*G);
disp(Pm);

如果相位裕度不足，我们可以通过增加控制器的增益或调整控制器的结构来提高相位裕度。

总结

通过以上步骤，我们成功地用MATLAB设计了一个满足性能要求的BUCK型DC/DC变换器控制系统。虽然过程中需要不断调整和优化，但MATLAB的强大功能让我们能够轻松应对这些挑战。希望这篇文章能对你有所帮助，如果你有任何问题或建议，欢迎在评论区留言！