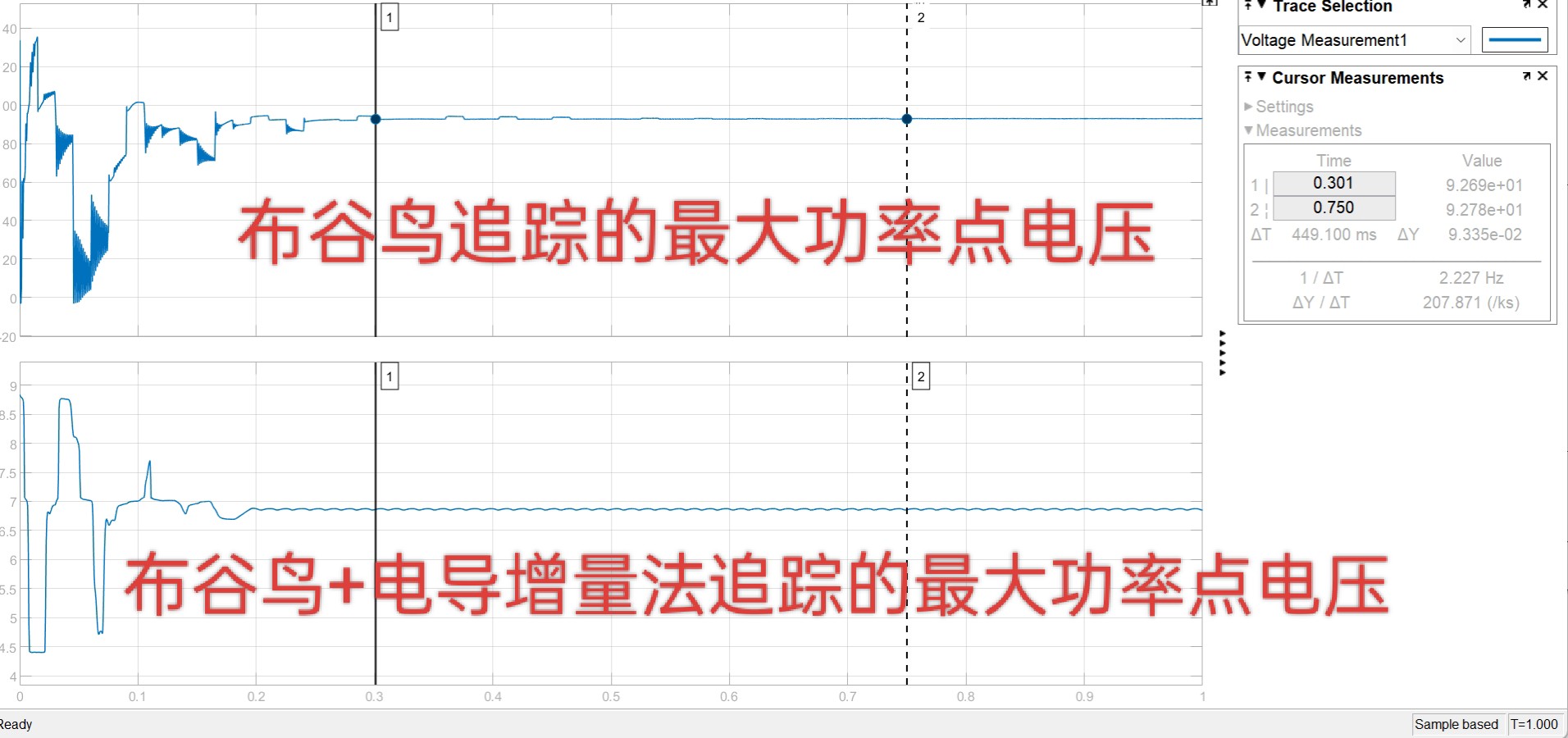
光伏MPPT仿真：布谷鸟算法的奇妙结合

光伏MPPT仿真布谷鸟算法MPPT对照布谷鸟算法结合电导增量法MPPT。可以看出布谷鸟结合电导增量法，追踪速度更快，波动更小。

在光伏系统中，最大功率点跟踪（MPPT）技术对于提高太阳能电池的转换效率至关重要。今天咱们来唠唠布谷鸟算法MPPT以及布谷鸟算法结合电导增量法MPPT的仿真对比，看看为啥后者表现更出色。

布谷鸟算法MPPT

布谷鸟算法（Cuckoo Search Algorithm）是一种受布谷鸟寄生行为启发的智能优化算法。在光伏MPPT的应用中，它通过不断搜索来找到光伏电池的最大功率点。

咱们简单用Python代码来模拟一下布谷鸟算法在MPPT中的基本框架（这里只是简单示意，实际情况会复杂得多）：

python 复制代码

import random


# 定义光伏电池功率计算函数，这里简单用一个线性关系代替实际复杂模型
def p_v(v):
    return 2 * v


# 布谷鸟算法参数
n = 10  # 鸟巢数量
alpha = 0.5  # 步长控制参数
pa = 0.25  # 发现外来鸟蛋的概率
max_iter = 100

# 初始化鸟巢位置（即电压值）
nests = [random.uniform(0, 10) for _ in range(n)]
best_nest_index = 0
for i in range(n):
    if p_v(nests[i]) > p_v(nests[best_nest_index]):
        best_nest_index = i
best_solution = nests[best_nest_index]

for _ in range(max_iter):
    for i in range(n):
        new_nest = nests[i] + alpha * random.gauss(0, 1)
        if p_v(new_nest) > p_v(nests[i]):
            nests[i] = new_nest
        if random.random() < pa:
            worst_nest_index = 0
            for j in range(n):
                if p_v(nests[j]) < p_v(nests[worst_nest_index]):
                    worst_nest_index = j
            nests[worst_nest_index] = random.uniform(0, 10)
    current_best_index = 0
    for i in range(n):
        if p_v(nests[i]) > p_v(nests[current_best_index]):
            current_best_index = i
    if p_v(nests[current_best_index]) > p_v(best_solution):
        best_solution = nests[current_best_index]


print("布谷鸟算法找到的最大功率点电压：", best_solution)

代码分析

功率计算函数p_v ：这里简单地用一个线性函数模拟光伏电池功率随电压的变化，实际中光伏电池的P - V特性是非线性且复杂的，需要更精确的模型。
初始化部分 ：设定了鸟巢数量n、步长控制参数alpha、发现外来鸟蛋概率pa以及最大迭代次数max_iter。初始化鸟巢位置，也就是可能的光伏电池电压值。
迭代过程 ：每次迭代中，对每个鸟巢位置进行更新，新位置基于当前位置加上一个随机步长。如果新位置对应功率更高则更新。同时，以一定概率pa随机替换最差鸟巢位置，以此探索新的解空间。

然而，单纯的布谷鸟算法在MPPT追踪过程中，可能存在追踪速度不够快，功率波动较大的问题。

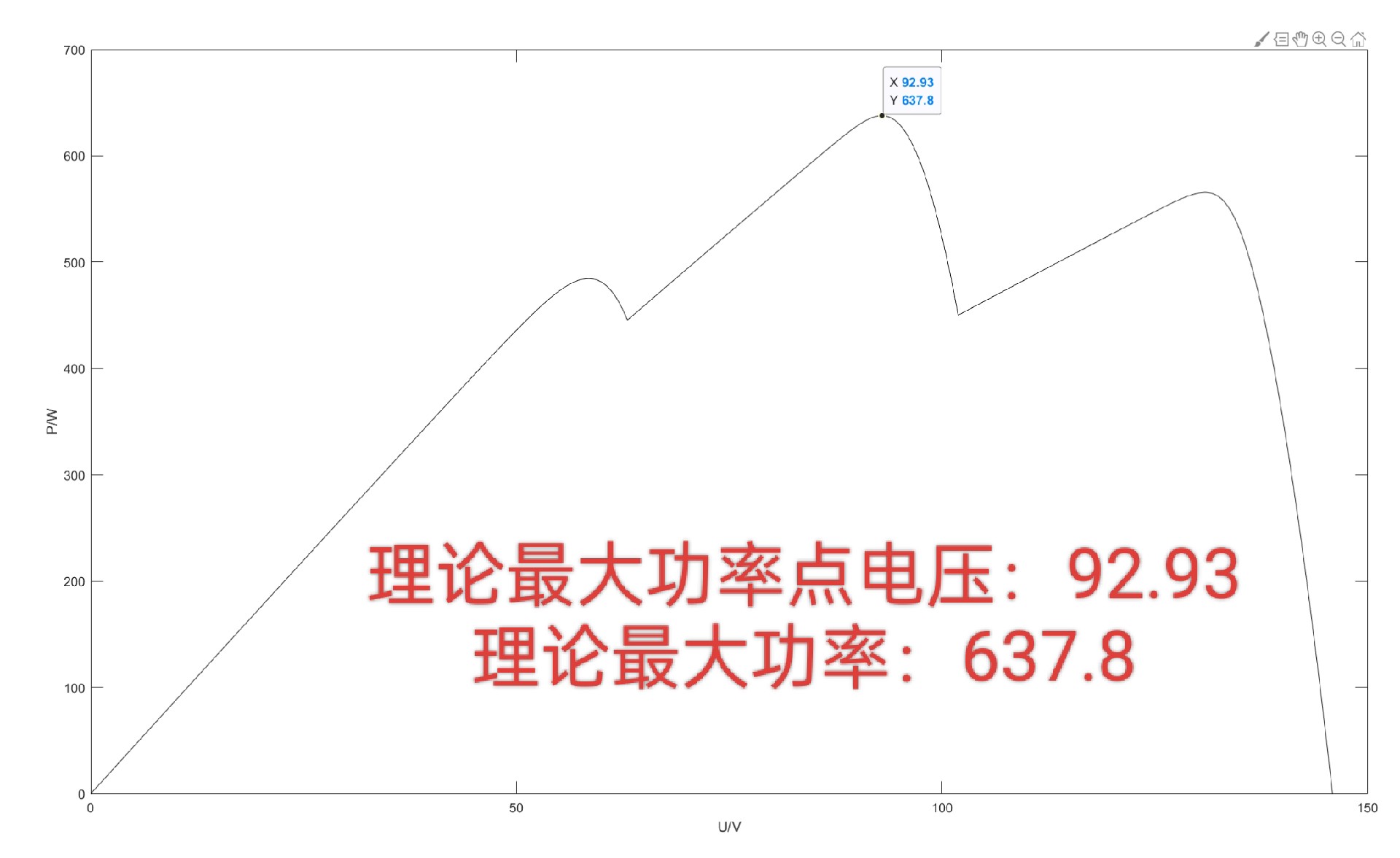
布谷鸟算法结合电导增量法MPPT

电导增量法（Incremental Conductance Method）是一种经典的MPPT方法，它通过比较电导的增量和瞬时电导来判断工作点与最大功率点的相对位置。将布谷鸟算法与之结合，能发挥两者优势。

下面来看结合后的代码示意（同样是简化示意）：

python 复制代码

import random


# 定义光伏电池功率计算函数，和上面一样简单模拟
def p_v(v):
    return 2 * v


# 布谷鸟算法参数
n = 10
alpha = 0.5
pa = 0.25
max_iter = 100

# 电导增量法参数
delta = 0.01  # 电压微小变化量

# 初始化鸟巢位置
nests = [random.uniform(0, 10) for _ in range(n)]
best_nest_index = 0
for i in range(n):
    if p_v(nests[i]) > p_v(nests[best_nest_index]):
        best_nest_index = i
best_solution = nests[best_nest_index]

for _ in range(max_iter):
    for i in range(n):
        v1 = nests[i]
        v2 = v1 + delta
        p1 = p_v(v1)
        p2 = p_v(v2)
        if (p2 - p1) / (v2 - v1) > p1 / v1:
            new_nest = v1 + alpha * random.gauss(0, 1)
        else:
            new_nest = v1 - alpha * random.gauss(0, 1)
        if p_v(new_nest) > p_v(nests[i]):
            nests[i] = new_nest
        if random.random() < pa:
            worst_nest_index = 0
            for j in range(n):
                if p_v(nests[j]) < p_v(nests[worst_nest_index]):
                    worst_nest_index = j
            nests[worst_nest_index] = random.uniform(0, 10)
    current_best_index = 0
    for i in range(n):
        if p_v(nests[i]) > p_v(nests[current_best_index]):
            current_best_index = i
    if p_v(nests[current_best_index]) > p_v(best_solution):
        best_solution = nests[current_best_index]


print("布谷鸟结合电导增量法找到的最大功率点电压：", best_solution)

代码分析

新增部分 ：引入了电导增量法的关键参数delta，用于计算电压微小变化时功率的变化。
位置更新判断 ：在每次更新鸟巢位置前，通过电导增量法的判断条件(p2 - p1) / (v2 - v1) > p1 / v1来决定新位置是在当前位置基础上增加还是减少步长。如果满足这个条件，说明功率随电压增加而增加，应往电压增大方向更新；反之则往电压减小方向更新。这样能更有针对性地搜索最大功率点，相比单纯布谷鸟算法盲目搜索，大大提高了追踪速度。
整体效果：由于结合了电导增量法对最大功率点方向的判断，布谷鸟算法在搜索过程中更"聪明"，追踪速度更快，并且功率波动也更小，更能稳定地跟踪到最大功率点。

通过仿真对比，很明显能看出布谷鸟结合电导增量法在光伏MPPT中有着更出色的表现，为光伏系统高效运行提供了更好的保障。在实际应用中，还需要根据具体的光伏电池特性和系统要求进一步优化算法和参数，以达到最佳效果。