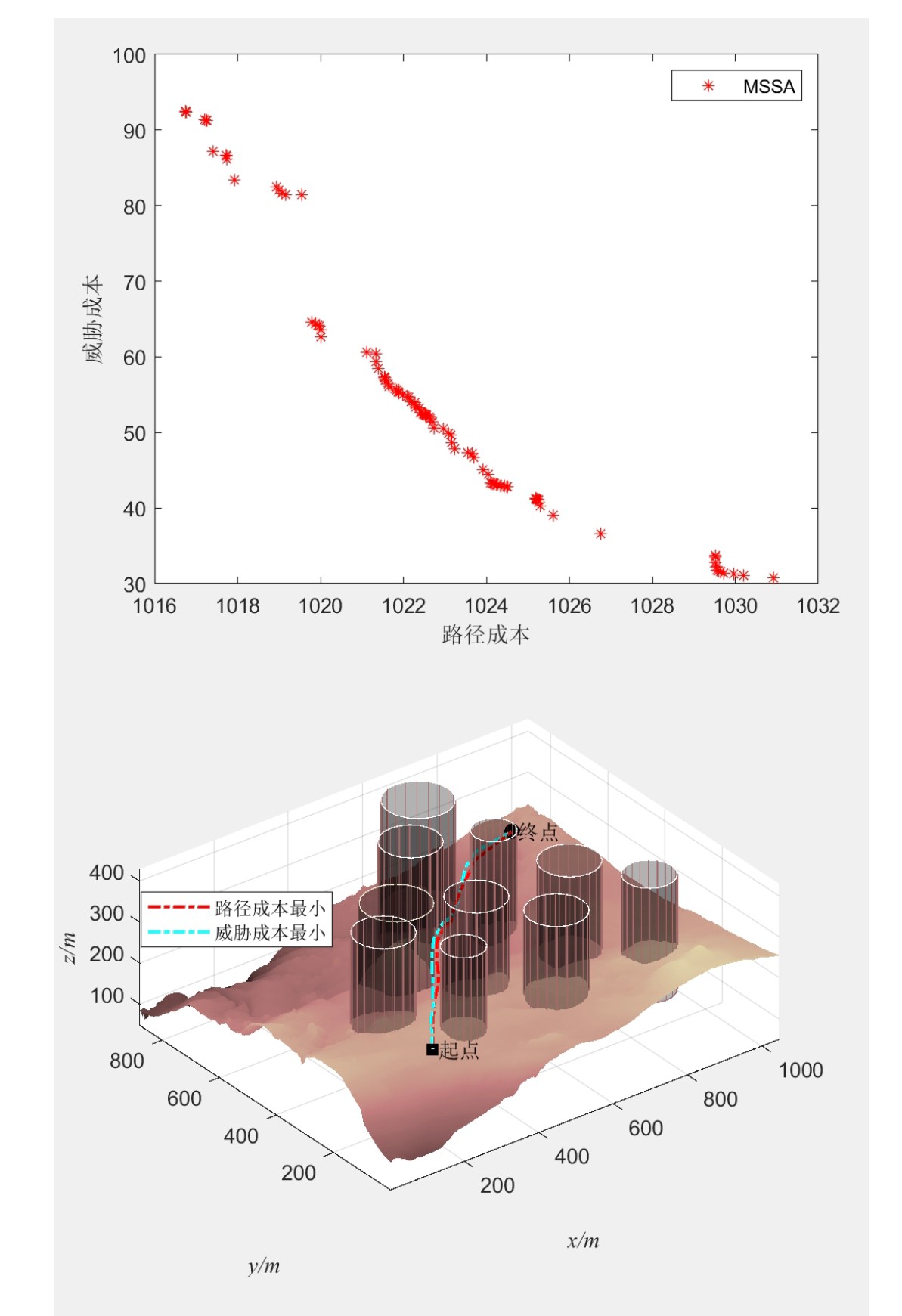
MSSA多目标樽海鞘优化算法求解无人机三维路径规划：MATLAB实战

多目标应用：MSSA多目标樽海鞘优化算法求解无人机三维路径规划（MATLAB代码）

在无人机应用领域，路径规划一直是个热门话题。当我们面临多目标的无人机三维路径规划任务时，传统方法可能会显得力不从心。今天就来聊聊用MSSA多目标樽海鞘优化算法解决这个问题，并且看看MATLAB代码实现的奇妙之处。

多目标路径规划难题

无人机在复杂的三维空间中飞行，要考虑躲避障碍物、节省能量、缩短飞行时间等多个目标。这就好比我们要在错综复杂的迷宫中，找到一条既最短、又最安全、还最节能的路径，难度可想而知。传统的单一目标规划算法在这里就不够用了，我们需要一种能同时权衡多个目标的方法，MSSA多目标樽海鞘优化算法就应运而生。

MSSA多目标樽海鞘优化算法原理

樽海鞘是海洋中的一种生物，它们在觅食时会形成特殊的结构和行为模式。MSSA算法就是模拟了樽海鞘的这种群体行为，在搜索空间中不断探索，寻找最优解。

在多目标的情况下，该算法会同时考虑多个目标函数，比如路径长度、与障碍物的距离等。通过不断迭代，让樽海鞘个体向更好的位置移动，逐渐收敛到一组非支配解，也就是帕累托前沿，这组解代表了不同目标之间的最佳权衡。

MATLAB代码实现

初始化部分

matlab 复制代码

% 参数设置
popSize = 50; % 种群大小
dim = 3; % 无人机路径的维度，这里是三维空间
maxIter = 100; % 最大迭代次数
lb = [0, 0, 0]; % 搜索空间下限
ub = [100, 100, 100]; % 搜索空间上限

% 初始化樽海鞘种群位置
position = repmat(lb, popSize, 1) + rand(popSize, dim).*(repmat(ub, popSize, 1) - repmat(lb, popSize, 1));

在这段代码中，我们首先设定了算法需要的一些基本参数，像种群大小popSize，这里设定为50个"樽海鞘"个体。dim表示无人机路径所在的三维空间维度。maxIter设置了最大迭代次数，这决定了算法的运行时间和搜索深度。lb和ub分别是搜索空间的下限和上限，这里假设无人机在一个边长为100的三维立方体内飞行。然后使用rand函数随机初始化了樽海鞘种群的位置，让它们均匀分布在搜索空间内。

目标函数定义

matlab 复制代码

% 定义目标函数，以路径长度和与障碍物距离为例
function [f1, f2] = objectiveFunctions(position)
    % 路径长度计算简化示例，假设起点为(0,0,0)
    f1 = sqrt(sum(position.^2, 2)); 
    % 与障碍物距离计算简化示例，假设障碍物在(50,50,50)
    obstaclePos = [50, 50, 50];
    f2 = sqrt(sum((position - repmat(obstaclePos, size(position, 1), 1)).^2, 2)); 
end

这里定义了两个目标函数，f1计算路径长度，这里简单假设起点是原点(0,0,0)，通过欧几里得距离公式计算路径长度。f2计算与障碍物的距离，假设障碍物在(50,50,50)，同样用欧几里得距离公式来衡量每个个体与障碍物的距离。实际应用中，目标函数的计算会更复杂，比如考虑真实的起点终点位置、多个障碍物等情况。

迭代更新部分

matlab 复制代码

for t = 1:maxIter
    % 计算每个樽海鞘的目标函数值
    [f1, f2] = objectiveFunctions(position);
    % 合并目标函数值
    objectives = [f1, f2];
    % 非支配排序
    [rank, crowdingDistance] = nonDominatedSorting(objectives);
    % 选择操作，这里简单示例，实际可更复杂
    [newPosition] = selection(position, rank, crowdingDistance);
    % 更新樽海鞘位置
    position = newPosition;
end

在迭代循环中，首先计算每个樽海鞘个体的目标函数值f1和f2，然后将它们合并成一个矩阵objectives。接着使用nonDominatedSorting函数进行非支配排序，这个函数会返回每个个体的等级rank和拥挤距离crowdingDistance。等级决定了个体在帕累托前沿中的位置，拥挤距离则用于在同一等级中选择分布更均匀的个体。最后通过selection函数进行选择操作，这里简单示例，实际应用中可以采用锦标赛选择、轮盘赌选择等更复杂的方法，选出下一代个体并更新种群位置。

总结

通过MSSA多目标樽海鞘优化算法和MATLAB代码的结合，我们可以有效地解决无人机三维路径规划中的多目标问题。当然，实际应用中还需要根据具体场景对代码进行更多优化和调整，比如更精确的目标函数建模、更复杂的选择和更新策略等。希望这篇文章能给对无人机路径规划感兴趣的小伙伴们一些启发，一起探索这个充满挑战又有趣的领域。