此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第三课的第二周内容,2.8的内容。
本周为第三课的第二周内容,本周的内容关于在上周的基础上继续展开,并拓展介绍了几种"学习方法",可以简单分为误差分析和学习方法两大部分。
其中,对于后者的的理解可能存在一些难度。同样,我会更多地补充基础知识和实例来帮助理解。
本篇的内容关于多任务学习,同样是在模型学习方式上的一种拓展。
1. 多任务学习
在上一篇的迁移学习中,我们知道,把一个任务的模型迁移到另一个任务中应用的前提是:两个任务的低层次特征十分相似。
现在在这个点子的启发下,又有人提出了新的想法:
既然多个任务的底层特征十分相似,那能不能在一个网络里同时训练针对这多个任务的模型?
这就是多任务学习的基本思想 。
理解多任务学习,你可以把它想象成让同一个大脑,同时学会几件相互关联的事情 。
在深度学习中,就是用一个模型 ,同时去做多个任务 ,而不是每个任务都训练一个独立模型。
为什么要这样做? 原因就是上面提到的,因为一些任务之间其实共享着大量底层特征。
举个例子:
在这种共享基础的前提下,单任务学习就像让学生分别学习语文、历史、写作,但明明这些科目都依赖阅读理解能力,结果你却让他重复学三遍阅读方法,显然不高效。
可能还是不太清楚,下面我们用课程里一个非常典型的例子来说明:
1.1 自动驾驶系统的路面识别
假设你正在开发一个自动驾驶系统,它需要识别:
- 行人检测
- 红绿灯识别
- 路标识别
- 车辆检测

现在,如果你为这些任务分别训练 4 个模型,那么它们都会学到:
- 图像边缘
- 物体轮廓
- 颜色分布
- 基本几何形状
而这些"底层特征"本质上是一样的。
在这时,多任务学习的做法是:让模型的前几层共享,后面的部分再根据不同任务分头进行。
继续上面的学生上课的例子,多任务学习就像:
先让学生统一上"基础课"(数学、逻辑、阅读),然后再按照专业分流各学科。
这样做有三个显著好处:
- 底层特征共享,训练更快
- 多个任务互相帮助,提高泛化能力
- 不用为每个任务单独准备海量数据
尤其是当某些任务数据较少时,多任务学习往往能让弱任务因为"借到其他任务的经验 "而表现更好。
了解了多任务学习的概念后,我们来看看它的适用范围。
1.2 何时适合多任务学习?
多任务学习不是万能的,它在以下条件下最有效:
- 多个任务之间具有相关性。
- 它们共享大量底层结构(如共同处理图像、共同处理语音)。
- 数据量有限,希望通过共享知识弥补某个任务的不足。
此外,机器终究是由我们人设计的,因此,对于是否适用多任务学习,一个最符合直觉的判断方式就是:如果一个人掌握任务 A 的知识后会更容易学会任务 B,那机器学习模型也可能如此。
例如:
- 识别猫的种类 + 判断猫的姿势
- OCR 文本识别 + 文本方向校正
- 情感分析 + 主题分类
- 车道检测 + 路面分割
但如果任务之间差异很大 ,比如"人脸识别"和"花卉识别",强行多任务反而会变成负担,让模型不知道优先学习什么,最终效果反而变差。
现在,我们就来看看到底如何实现多任务学习。
1.3 多任务学习的实现逻辑
实际上,我们在多值预测与多分类那一节里就简单提到过这部分内容,现在才正式展开。
回忆一下最初的内容,在单任务学习中,我们的数据通常表示为一组样本对:
\[(x^{(i)}, y^{(i)}) \]
其中
- \(x^{(i)}\) 是输入样本
- \(y^{(i)}\) 是样本对应的"单个任务标签"
但在自动驾驶系统中,一张路面图片往往需要同时识别多个内容 ,这意味着对同一个输入 \(x^{(i)}\),原本只有一个标签,现在变成了多个标签。
在开始前,再用我们的猫狗分类器举例再理解一下这句话:
原本我们的数据集样本中只会存在猫或者狗中的一种,相应的标签自然就只有猫或狗。
现在任务改变,样本中出现了猫和狗的"合照",标签自然也会增加,实现同时识别猫和狗的多任务学习。
举完这个简单的例子后,我们来正式展开这一部分。
(1) 多个任务的标签如何组织?
继续用前面的自动驾驶例子。现在一张图像 \(x^{(i)}\),我们需要它同时给出:
- 有没有行人(是/否)
- 有没有车辆(是/否)
- 有没有路标(是/否)
- 有没有红绿灯(是/否)
这里先强调一下,我们只是使用这个语境来了解多任务学习,实际逻辑远比这要复杂。
现在,单任务的标签 \(y^{(i)}\) 就不够用了,我们需要让它变成一"组"标签,就像这样:
\[y^{(i)} = (y^{(i)}_1, y^{(i)}_2, y^{(i)}_3, y^{(i)}_4) \]
其中 :
- \(y^{(i)}_1\):行人检测
- \(y^{(i)}_2\):车辆检测
- \(y^{(i)}_3\):路标检测
- \(y^{(i)}_4\):红绿灯检测
于是,从结构上看,\(y^{(i)}\) 就不再是一个标量,而是一个代表"任务集合"的向量。
来看一个实例:
假设现在有一张路口照片 \(x^{(i)}\),内容如下:
- 画面中有行人。
- 画面中也有车辆。
- 没有看到任何路标。
- 画面中有红绿灯。
那么,这张图片的多任务标签就是:
\[y^{(i)} = (1, 1,0, 1) \]
而如果让任务再复杂一些,我们还会具体对红绿灯进行三分类,于是又加入了独热编码,例如:
\[\text{green} = (0, 0, 1) \]
在这种情况下,这张图片的最终标签就变成了:
\[y^{(i)} = (1, 1, 0, (0, 0, 1)) \]
总之,一个输入 \(x^{(i)}\),多行标签一起出现,这就是多任务学习在标签维度上的直接体现。
说到这里,你可能会有这样一个问题,多任务学习与应用独热编码的多分类都把标签从标量变成了向量,这不会混淆吗? 我们在这个问题上简单展开一下。
(2)多标签与应用独热编码的多分类辨析:互斥性
在多任务学习中,经常会看到这样的表达:
- 某些任务是"多标签"
- 某些任务会用独热编码
- 两者都长得像一串 \((0,1)\) 组成的向量
就像刚刚的:
\[y^{(i)} = (1, 1, 0, (0, 0, 1)) \]
虽然它们看起来很像,但本质完全不同 。
依旧以自动驾驶为例,你要判断一张图片里:
- 有没有人(是/否)
- 有没有车(是/否)
- 有没有路标(是/否)
- 有没有红绿灯(是/否)
这四件事之间互不影响 。
画面里可以同时出现行人 + 车辆 + 红绿灯,也可以一个都没有。
因此,每个标签都是一个独立的二分类任务:
\[y^{(i)} = (y^{(i)}_1, y^{(i)}_2, y^{(i)}_3, y^{(i)}_4),\quad y^{(i)}_k \in {0,1} \]
这里的四个 \(y^{(i)}_k\) 都是"自由的",可以同时为 1 。
也就是说多任务学习的任务间没有互斥性,sigmoid更适用这种逻辑。
现在再说说多分类 :
红绿灯状态只有三种:红、黄、绿 。
它们不能同时出现,因此需要用独热编码:
\[\text{red}=(1,0,0),\quad \text{yellow}=(0,1,0),\quad \text{green}=(0,0,1) \]
这个编码的特点是:存在互斥性 ,向量中只能出现一个 1,因此通常接 softmax 激活函数。
如果你有点忘了,它第一次出现在这里: 独热编码
因此,这不是"多标签",而是"单标签多分类"。
总结一下,区分二者的关键就是标签间的互斥性 ,即是否允许多个标签同时为 1。
能同时为 1 的就是"多标签",不能同时为 1 的就是"多分类(独热编码)"。
(2) 多任务学习的模型结构长什么样?
我们先按照课程里的内容,看一看最简单的多任务学习模型 长什么样子。
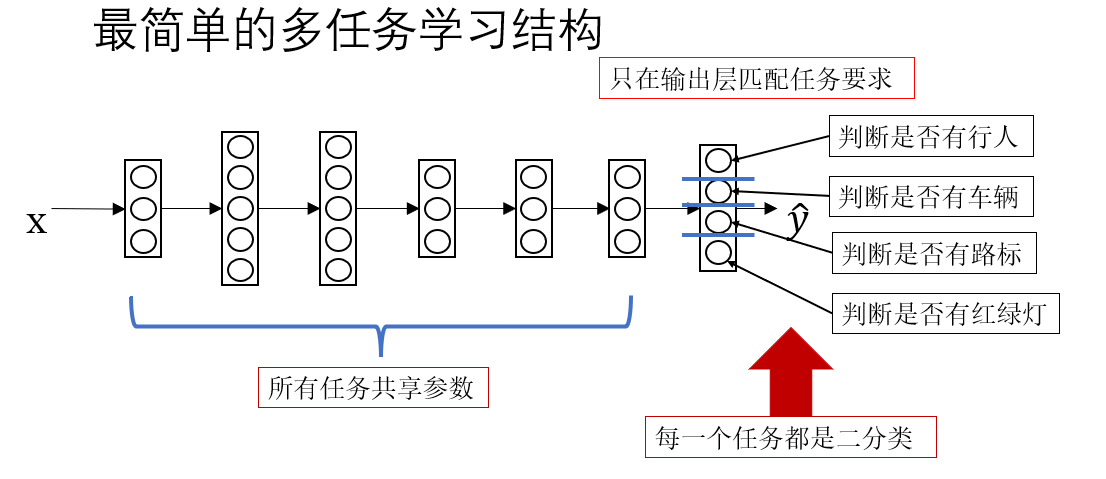
很显然,这和我们之前的模型并没有什么区别,只是根据任务要求给输出层的每个节点匹配了不同的语义。实际上,在真正的多任务学习里,这种结构略显简陋。
现在我们来看下一步扩展:
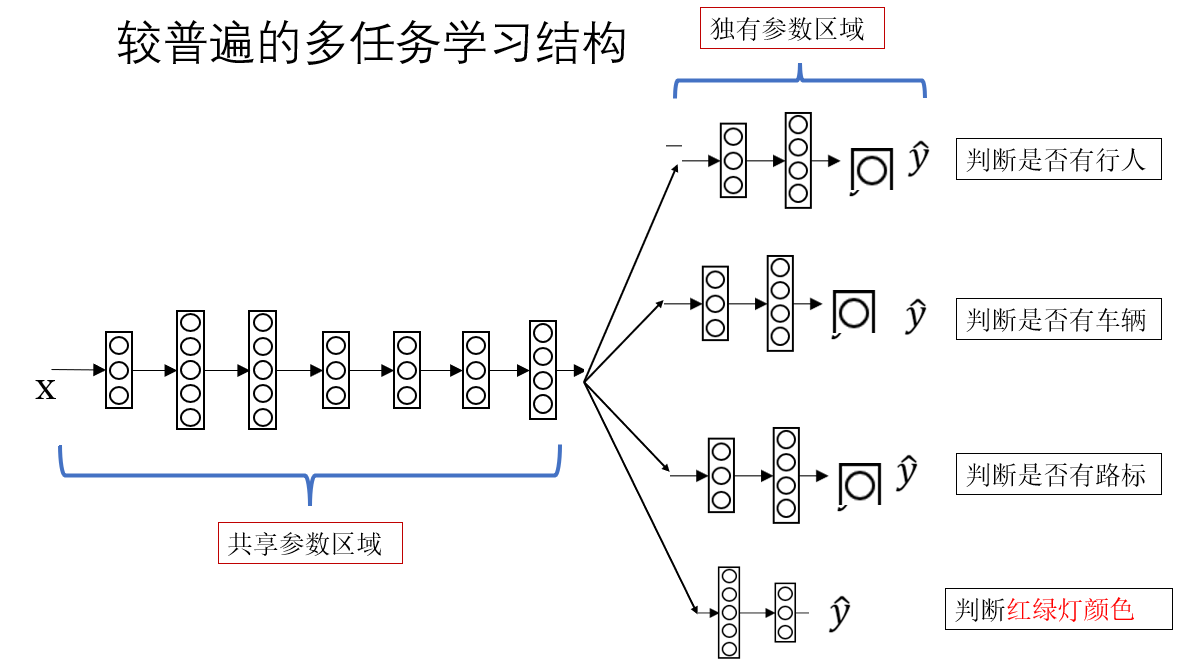
这种结构就是和上面的最大区别就在于这种"前面共享、后面分头 "的结构。
模型最前面的几层负责提取底层特征,之后,不同任务会接上不同的"小网络模块",我们称为 task head(任务头)。
在这里就是:
- 行人检测 head:判断有没有行人
- 车辆检测 head:判断有没有车
- 路标检测 head:判断是否存在路标
- 红绿灯 head:做红/黄/绿的分类
这四个任务头不会共享参数,它们各自学习怎么从底层特征里找出与自己任务相关的特征。
所以多任务结构能带来:
- 训练更快(底层共享)
- 泛化更强(任务间互相帮助)
- 对少数据任务更友好(能借其他任务的信息)
继续打比方:
模型前面像一位"通识教育老师"教基础知识;
模型后面像四位"专业课老师"分别教行人检测、车辆检测、路标识别、红绿灯识别。
正向传播说完了,现在来看看反向传播。
(3)多任务模型的损失函数整合
现在,每个任务都有自己的损失:
\[L_1, L_2, L_3, L_4 \]
而多任务学习的整体目标是同时优化所有任务,因此最终损失通常是:
\[L = L_1 + L_2 + L_3 + L_4 \]
与此同时,不同任务可能重要性不同,因此有时会给部分任务更大的权重:
\[L = \alpha_1 L_1 + \alpha_2 L_2 + \alpha_3 L_3 + \alpha_4 L_4 \]
你可以把它理解成学生的期末总成绩由多门课程的成绩共同决定,有的科目是必修,就权重更高。
最后,多任务学习就像一棵树:
- 根和树干:共享的前几层(基本特征提取)
- 分叉的树枝:根据不同任务分成多个 "Head"
- 每个任务的输出叶子:分类、回归或特定目标
因此这种结构也被称为 Shared-bottom(共享底层)模型。
2.总结
| 概念 | 原理 | 比喻 |
|---|---|---|
| 多任务学习的适用条件 | 多个任务需要共享大量底层特征;任务之间具有关联性;数据量有限时共享结构能互相补充。 | 像学生学习语文、历史、写作,三者都依赖阅读能力,因此可以在同一门"基础课"中打底,再各自深入。 |
| 多标签(多任务) vs. 独热编码多分类 | 多标签任务中,每个标签彼此独立,可以同时为 1;独热编码多分类具有互斥性,只能出现一个 1。 | 多标签:一个人可以同时"会游泳、会跑步";独热编码:一个人"只能是男或女,不会同时是两者"。 |
| 多任务学习的标签结构 | 单一标签由标量变成向量:\(y^{(i)} = (y^{(i)}_1, y^{(i)}_2, \dots)\);互相独立,各自对应不同的任务头。 | 就像一次体检,一项检查报告里同时包含身高、体重、视力、血压,每一项互不干扰。 |
| 共享底层 + 多任务 Head 的结构 | 模型前几层负责学习共同底层特征;后面不同 Head 仅负责学习自己任务特有的模式。 | 前面像"通识课老师"教基础知识;后面像"专业课老师"各自教授专项技能。 |
| 多任务损失函数的组合方式 | 多任务损失通常相加:\(L = L_1 + L_2 + L_3 + \dots\);必要时加入权重:\(L = \alpha_1 L_1 + \alpha_2 L_2 + \dots\)。 | 像期末总成绩由语数外等各科成绩共同组成,有些科目(如数学)权重更高。 |