目录
隐式马尔科夫模型的定义
隐式马尔科夫模型,简称HMM(Hidden Markov Model), 是一种基于概率的统计分析模型,用来描述一个系统隐性状态的转移和隐性状态的表现概率。
区别
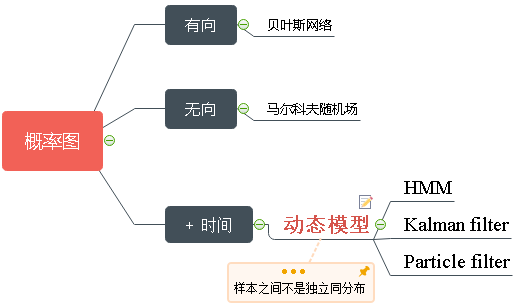
隐马尔可夫模型(HMM)和贝叶斯分类器(以朴素贝叶斯为代表)虽然都基于贝叶斯定理,但它们的设计目的、数据假设和应用场景有本质区别。
最主要的区别在于 数据的结构和依赖关系 :
隐马尔科夫模型:像在分析一个有顺序的句子。它认为每个单词(观测)背后有一个隐藏的词性(状态),并且当前的词性会受到上一个词性的影响。它要同时推断这个隐藏的状态序列。
朴素贝叶斯:像在分析一袋独立的单词(词袋模型)。它看每个词出现的概率来判断这袋词属于哪个类别(如垃圾邮件/正常邮件)。
下面不谈原理,只能谈点流程。
URL为什么要分类?
在HTTP流量分析的时候,一些城市、分支机构、时间的URL需要分类出来过滤掉。
留下一些类似功能接口的URL。
XSS攻击荷载的特征
ounter(lineounter(lineounter(lineounter(lineounter(lineounter(line
<src>
<script>
<alert>
http://
<img>
onerror流程介绍
预测人心情的案例,它假设有一个我们看不见的状态链(比如情绪),这个状态链是按照马尔可夫性(当前状态只依赖于前一个状态)变化的,并且每个状态会产生一个观测值(比如行为)。我们通过观测值来推测状态链,或者评估观测序列的概率等。
你可以看见朋友小明的动作(看得见),要去猜他背后的心情(看不见),而且心情会每天变化。
下面梳理一些设定的规则:
小明的动作:吃饭、玩游戏、睡觉
小明的心情:开心、难过
规则①:心情会变化(转移概率)
如果今天开心:
- 明天继续开心:70%
- 明天变成难过:30%
如果今天难过:
- 明天继续难过:60%
- 明天变成开心:40%
规则②:心情决定动作(发射概率)
开心时:
吃饭:20%
玩游戏:70%
睡觉:10%
难过时:
吃饭:50%
玩游戏:10%
睡觉:40%
规则③:第一天心情(初始概率)
开心:60%
难过:40%
观察到小明三天的动作:玩游戏 → 睡觉 → 吃饭
计算:
第1步:猜第一天心情
小明第一天在玩游戏:
如果是开心:60%×70% = 42%
如果是难过:40%×10% = 4%
→ 所以第一天最可能是开心!
第2步:猜第二天心情
小明第二天在睡觉:
情况A:第一天开心→第二天开心:
42% × 70% × 10% = 2.94%
情况B:第一天开心→第二天难过:
42% × 30% × 40% = 5.04%
情况C:第一天难过→第二天开心:
4% × 40% × 10% = 0.16%
情况D:第一天难过→第二天难过:
4% × 60% × 40% = 0.96%
最大的是5.04% → 所以第二天是难过,而且是从第一天开心变来的。
第3步:猜第三天心情
小明第三天在吃饭:
(只跟踪最大概率的路径:开心→难过→?)
从第二天难过开始:
变开心:5.04% × 40% × 20% = 0.4032%
变难过:5.04% × 60% × 50% = 1.512%
最大的是1.512% → 所以第三天继续难过。

Reference
用隐式马尔科夫模型检测XSS攻击Payload
https://mp.weixin.qq.com/s/iSrV95K75EwDAGVJGdFRTQ
【整理】图解隐马尔可夫模型(HMM)
https://developer.aliyun.com/article/441100