由雷诺数公式
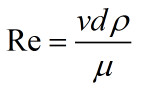
流速(v)、管道直径(d)、流体的密度(ρ)、动力粘度(μ)
30摄氏度水在内径0.1m的管子里流动,保持层流的最大流速1.8厘米每秒
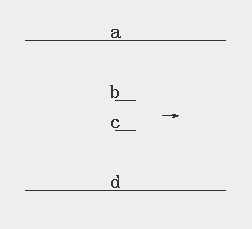
假设液体内分子团以二维片状存在,在管子的近中心有两片b和c,让他们在粘性的作用下绕对方旋转
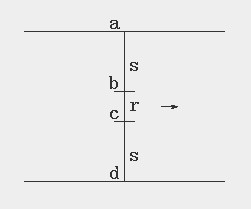
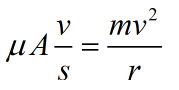
2s=d
逃逸半径
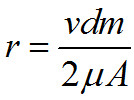
已有报道最小的水珠可由5个水分子构成,
设这5个分子构成的分子片为
|---|---|---|
| 1 | | 1 |
| | 1 | |
| 1 | | 1 |
设每个小方形的边长为0.4*1E-9m,这个片的面积为1.44*1E-18m*m.逃逸速度不会小于最大层流速度,设V就是0.018m/s,代入
|---|----------|-----------|-----------|------|
| v | 0.018 | m/s | | |
| d | 0.1 | m | | |
| p | 1000 | kg/m^3 | | |
| u | 0.000798 | NS/(m*m) | | |
| A | 1E-09 | 1.44 | 1.44E-18 | m*m |
| m | 2.99E-26 | 5 | 1.495E-25 | kg |
得到逃逸半径r为1.17E-7m,117nm
颗粒间的范德华力作用距离可以达到100nm,所以117nm这个值至少在量级上是有可能的。 也就是假设湍流的初始漩涡就在100nm量级,范德华力的作用范围之内,宏观可见的巨大漩涡只是小漩涡多次碰撞放大的效果。
这也提示如果运动速度过小,逃逸半径仍然在范德华力作用范围内分子片可能会被重新捕获,所以流动仍然规则。
或者反过来,因为范德华力的作用距离总有一个最大值,只要流速足够大逃逸现象就一定会发生。
25摄氏度时甲醇的密度是791kg/m^3,动力粘度是0.00055 NS/(m*m),管径0.1m,雷诺数为2300.计算保持层流的最大速度是0.0159m/s
假设甲醇的最小液滴也是5个分子构成
|---|----------|---------|------------|------|---|
| v | 0.0159 | m/s | | | |
| d | 0.1 | m | | | |
| p | 791 | kg/m^3 | | | |
| u | 0.00055 | NS/(m*m) || | |
| A | 1E-09 | 3.3 | 3.3E-18 | m*m | |
| m | 5.32E-26 | 5 | 2.6578E-25 | kg | |
| | | | | | |
计算r=1.16416E-07m
如果让最小逃逸半径都是117nm左右,则甲醇分子片的面积要有约3.3平方纳米,比水的要大。
20摄氏度是乙醇的密度是789.3kg/m^3,动力粘度是0.001074 NS/(m*m),管径0.1m,雷诺数为2300.计算保持层流的最大速度是0.031m/s
假设乙醇的最小液滴也是5个分子构成
|---|-------------|---------|------------|------|---|
| v | 0.031296085 | m/s | | | |
| d | 0.1 | m | | | |
| p | 789.3 | kg/m^3 | | | |
| u | 0.001074 | NS/(m*m) || | |
| A | 0.000000001 | 4.7 | 4.7E-18 | m*m | |
| m | 7.6412E-26 | 5 | 3.8206E-25 | kg | |
| | | | | | |
计算r=1.18437E-07m
面积是4.7平方纳米
|------|-----|-----|--------|
| 水 | 甲醇 | 乙醇 | |
| 1.44 | 3.3 | 4.7 | nm*nm |
分子片的面积由水到甲醇到乙醇依次增大,至少这个顺序是合理的。
当然这里甲醇的最小分子片也可能由10个分子构成
|---|-------------|---------|------------|------|---|
| v | 0.0159 | m/s | | | |
| d | 0.1 | m | | | |
| p | 791 | kg/m^3 | | | |
| u | 0.00055 | NS/(m*m) || | |
| A | 0.000000001 | 6.6 | 6.6E-18 | m*m | |
| m | 5.31561E-26 | 10 | 5.3156E-25 | kg | |
| | | | | | |
计算r=1.16416E-07m
如果逃逸半径固定这个假设是成立的,总可以由逃逸速度得到质量面积比m/A,而质量一定是量子化的,在m/A已知的条件下可能推出来分子片的结构。
或者即便r也有一个范围,但只要能测出v和r的值就可以得到质量面积比,这样由宏观的v和r去推断片的结构总有可能。