继续用交错堆叠的结构估计水分子间距。
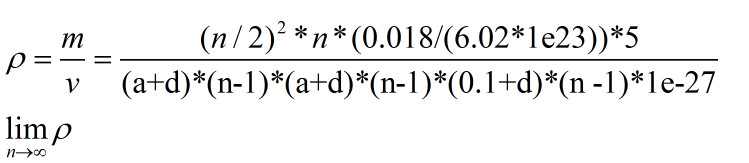
设水分子由5个构成一片,片内的分子由饱和氢键连接,片与片之间以范德华力相互作用。
已知水在1个大气压,4摄氏度时密度为999.972kg/m^3,
假设其分子片的间距是0.1nm,片的尺寸是a*a*0.1nm^3
|-------------------------------------------------------|
| d=0.1 |
| |
| f1=(n/2)*(n/2)*n*(0.018/(6.02*1e23))*5 |
| f2=(a+d)*(n-1)*(a+d)*(n-1)*(0.1 +d)*(n-1)*1e-27 |
| |
| f3 = sympy.limit(f1/f2, n, sympy.oo) |
| print( f3) |
| f3=999.9714 |
计算得到a=0.332299
水在1个大气压,100摄氏度时密度为958.345kg/m^3,
因为压力相同,设d不变
|-------------------------------------------------------|
| d=0.1 |
| |
| f1=(n/2)*(n/2)*n*(0.018/(6.02*1e23))*5 |
| f2=(a+d)*(n-1)*(a+d)*(n-1)*(0.1 +d)*(n-1)*1e-27 |
| |
| f3 = sympy.limit(f1/f2, n, sympy.oo) |
| print( f3) |
| f3=958.3442 |
计算得到a=0.341588
二者分子片中分子间距的差为0.01nm,差不多为氢键O-H...键长的1/27.是氢氧键键长的约1/10.所以这个结果可以理解为,由于温度的增加导致分子热运动加剧,分子间的距离变大,分子片变大,最终使液体密度变小。
虽然水分子不一定是这样交错堆在一起,也不一定每片有5个分子,但这个假设可以合理解释这个现象。所以有理由猜测压力作用于分子片间距,温度作用于分子片中分子间距。
设分子片的长宽高是a,b,c总的体积是
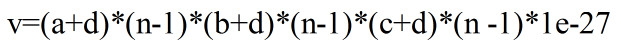
其中a+d一定等于a与某个实数的积
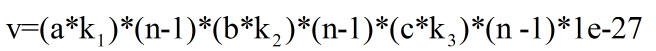
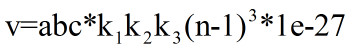
温度作用于分子,让分子振动范围变化,并导致体积变化
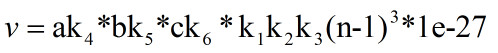
得到
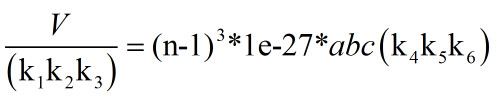
因为压力越大,d越小所以有
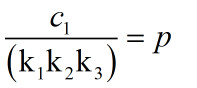
因为温度越大体积越大,
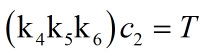
所以
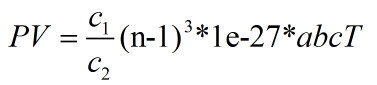
这一计算暗示压力和温度的微观对应量就是分子片的间距d和分子片中分子的间距d1, 所以如果d1变化,d不变就是等压过程,如果d变化d1不变就是等温过程,如果d变大d1变小,或者d变小d1变大就是等容过程。
在温度不变的条件下,增加压力让气体液化,就是保持d1不变,让d减小。
在压力不变的条件下,增加温度让液体气化,就是保持d不变,让d1变大。
假设随着压力的增加d不会无限制的变小会有一个极限dmin,同样随着温度的增加d1也不会无限制的变大也有一个极限d1max,这样就存在一个压力区间和一个温度区间,在这个区间内d=dmin,d1=d1max,在这个区间内改变压力和温度d,d1不会有任何变化,所以这个条件下没有气液的差别。
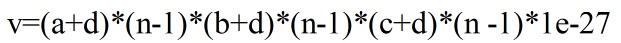
这一算法对存在微观分子片的气体液体都成立,
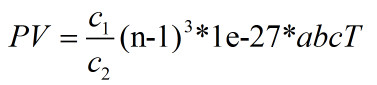
这一算法对气体液体也应该都成立。
在水的相图中固体有很多种,如果气液相变是由于d和d1的变化导致,那有理由猜测固体的变化同样是由于原子距离的变化导致的,只不过晶格的种类可能有很多,所以导致更多的d,因此随着压力的变化导致固体有更多的变化